Рассмотрен метод расчёта температурного и влажностного режима внутри объёма бронетанковой техники при длительном хранении в эксплуатационных условиях Вьетнама.
Ключевые слова: бронетанковая техника, длительное хранение, температурный и влажностный режим, теплообмен
Климатические условия различных районов, время года и суток, погода оказывают большое влияние на сохраняемости бронетанковой техники при длительном хранении. Летний и зимний периоды эксплуатации машин определяются температурой, влажности наружного воздуха. Особенностями эксплуатации машин в летних условиях являются: высокая температура окружающего воздуха; сильная запылённость воздуха, особенно при движении в колонне; повышенный уровень осадков.
Большая влажность воздуха, особенно в сочетании с высокой температурой, может быть причиной усиления коррозии деталей и механизмов. Рассмотрим теперь более подробно, как вышеперечисленные условия влияют на работоспособность систем и агрегатов бронетанковой техники при длительном хранении. Так, вследствие чрезмерных напряжений в металле головок блоков и силовых шпилек, имеющих разные коэффициенты линейного расширения, происходит смятие алюминиевых прокладок, ослабляется их затяжка.
Температурный режим во внутренних объемах образцов объекта формируется в условиях переменного режима погоды, задержки в передаче внешних воздействий к внутренним объемам (прогрев танка Т-55 требует и длительного времени, и значительных затрат энергии), неплотности стыковых элементов конструкции, сложности формы и конструкции оболочки.
Таблица 1
Температурный ивлажностный режим вэксплуатационных условиях Вьетнама в 2015г.
|
Месяц |
Температура (Град) |
Влажность (%) |
Солнце (час/месяц) |
|
1 |
18,1 |
78 |
98,9 |
|
2 |
19,2 |
82 |
43,8 |
|
3 |
21,6 |
88 |
32,4 |
|
4 |
25,4 |
78 |
114,3 |
|
5 |
30,6 |
75 |
204,7 |
|
6 |
30,9 |
75 |
178,0 |
|
7 |
30,4 |
72 |
124,0 |
|
8 |
29,0 |
82 |
157,7 |
|
9 |
28,5 |
83 |
101,0 |
|
10 |
27,2 |
72 |
139,0 |
|
11 |
24,6 |
80 |
83,6 |
|
12 |
18,5 |
75 |
44,6 |
При периодических изменениях температуры и в условиях пониженной влажности интенсивность коррозионных процессов во многих случаях превышает интенсивность коррозии при повышенной влажности и относительно стабильной температуре.
Целью настоящей работы является расчёт температурного и влажностного режима внутри бронетанковой техники при длительном хранении. Эта играет очень важную роль для управления параметров воздуха внутри бронетанковой техники при длительном хранении в эксплуатационных условиях Вьетнама.
Основание
При длительным хранениии бронетанкой техники существуют влияния некоторых факторов на внешнюю поверхность: тепловое излучение Солнца W1; тепловое излучение в мировое пространство или на окружающие предметы, имеющие более низкую температуру поверхности W2; конвективный тепловой поток от движущегося атмосферного воздуха или циркуляции воздуха, формирующейся в боксах W3; тепловое излучение днища на поверхность Земли W4; тепловой поток в результате фильтрации воздуха через открытые проемы или неплотности в люках W5.
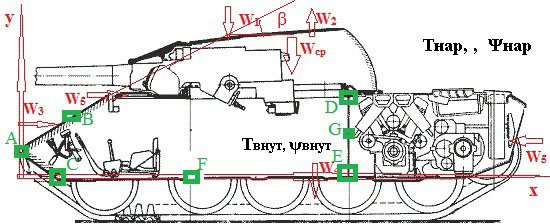
Рис. 1. Схема тепловых воздействий на бронетанковую технику в процессе длительного хранения
Под воздействием потоков W1, W2, W3, W4 формируется температура поверхности внешних элементов образцов БТВ. За счет теплопередачи через элементы конструкции оболочки теплота поступает к внутреннему объему (тепловой поток W). Под воздействием W + W5 формируется режим изменения температуры t и влажности Ω воздуха во внутренних объемах танка.
Теплообмен между двумя воздушными средами, разделенными жесткой многослойной конструкцией, количественно может быть оценен исходя из законов конвективного, кондуктивного и радиационного переносов теплоты. Перенос теплоты от воздуха к поверхности и наоборот определяется закономерностями конвективного переноса и радиационного теплообмена поверхности с окружающими предметами, трехатомными газами окружающей атмосферы, а для наружных поверхностей — еще и излучением в мировое пространство. С учетом традиционной модели теплопроводности в пограничном слое конвективный перенос на поверхностях моделируется с помощью искусственно вводимых понятий о теплоотдаче или тепловосприятии.
При определении математической модели теплопередачи через корпус и башню образцов танка принимаем следующие условия:
– конструкции являются многослойными (рис. 1), причем на поверхностях контакта слоев принимаются граничные условия четвертого рода; на внешних границах оболочки — третьего рода, осложненные радиационным переносом теплоты;
– теплотехнические характеристики материалов слоев не зависят от влажности и температуры и не изменяются во времени;
– в формировании теплового баланса рассматриваемых объемов учитывается фильтрация воздуха через щели в сопрягающихся элементах конструкции;
– башня и корпус представляют собой фигуры, состоящие из прямоугольных пластин, параллельных или расположенных под различными углами друг к другу;
– температурное поле рассматривается для одного меридионального
сечения по корпусу и по этой причине принимается двумерным.
Последнее замечание требует дополнительного пояснения. Контуры рассматриваемых танков имеют сложную трехмерную форму, математическое описание которой возможно, но связано с огромными физическими и умственными затратами. Этот фактор, а также некоторая условность всякой модели формирования режима погоды или микроклимата в месте хранения танков требуют разумного упрощения задачи. По этой причине в работе принята двумерная модель температурных полей, которая позволяет выявить качественную картину процессов формирования микроклимата во внутренних объемах объектов в процессе хранения и на основании экспериментальных измерений скорректировать полученные результаты.
Это утверждение основано на теореме, согласно которой решение трехмерной задачи теплопроводности может быть представлено в виде произведения решений для одномерных задач, т. е. Ѳ(х, у, z, τ) = Ѳ(х, τ).Ѳ(у, τ).Ѳ(z, τ). Отсюда следует, что всегда можно найти функцию, связывающую решение двумерной и трехмерной задач.
Процессы теплообмена между танком и воздушной средой происходят при нестационарном режиме. При исследовании процессов нестационарной теплопроводности искомой величиной является распределение температуры во времени и пространстве, т. е. функция вида.
T=φ(x,y,z,τ) (1)
где х, у, z — пространственные координаты; τ — время, с.
Уравнение нестационарной теплопроводности в двумерном представлении при отсутствии источников и стока теплоты имеет вид
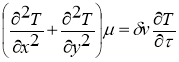 (2)
(2)
Здесь Т — температура, К; μ — коэффициент теплопроводности, Вт/(м. К); v — объемная масса, кг/м3; δ — теплоемкость, Дж/(кг.К).
Решение (2), соответствующее рассматриваемой задаче, получено при следующих начальных условиях:
Т0=Т(х,у,0)(3)
Граничные условия определяют закономерность изменения значений переменных на границах расчетного пространства и в данном случае состоят в задании условий теплового взаимодействия тела с окружающей воздушной средой:
![]() (4)
(4)
![]() (5)
(5)
Где ![]() — градиент температуры по нормали к рассматриваемой поверхности; μвнут, μнар — коэффициент теплопроводности слоя сопрягающегося соответственно с внутренним и наружным воздухом; ψвнут, ψнар — то же теплообмена на поверхности, сопрягающейся соответственно с внутренним и наружным воздухом; W6 — суммарный эффект от излучения на внешнюю поверхность Солнца (прямая и рассеянная радиация) и излучения внешней поверхности на окружающие предметы и строения, а также в мировое пространство; Твнут, Тнар — температура поверхности, сопрягающейся соответственно с внутренним и наружным воздухом; tвнут, tнар — то же наружного и внутреннего воздуха.
— градиент температуры по нормали к рассматриваемой поверхности; μвнут, μнар — коэффициент теплопроводности слоя сопрягающегося соответственно с внутренним и наружным воздухом; ψвнут, ψнар — то же теплообмена на поверхности, сопрягающейся соответственно с внутренним и наружным воздухом; W6 — суммарный эффект от излучения на внешнюю поверхность Солнца (прямая и рассеянная радиация) и излучения внешней поверхности на окружающие предметы и строения, а также в мировое пространство; Твнут, Тнар — температура поверхности, сопрягающейся соответственно с внутренним и наружным воздухом; tвнут, tнар — то же наружного и внутреннего воздуха.
На поверхностях контакта слоев задавались условия четвертого рода (условия сопряжения), которые сводятся к одновременному заданию равенства температур и тепловых потоков на границе раздела:
![]() (6)
(6)
![]() (7)
(7)
По линии сопряжения расчетной области с другими элементами БТВ (у = 0) принято условие:
W5x # 0, W5y=0 (8)
Условия (3)-(8) допускают различные модификации в зависимости от конкретных физических условий на границе раздела сред. Так, при хранении образцов танка в закрытых помещениях значение Wизл будет существенно отличаться от численного значения этого параметра для условий открытого хранения. Корпус и башня танка являются многослойной оболочкой (надбой, броня, подбой). Контакт между этими средами не идеален вследствие неплотности соприкосновения поверхностей. Термическое сопротивление контакта в отдельных случаях может быть пренебрежимо малым, но иногда общее тепловое сопротивление многослойной стенки благодаря сопротивлению в местах контакта увеличивается в несколько раз.
Теплофизические коэффициенты, входящие в уравнения 2–7, определялись как экспериментально, так и теоретически.
Получить решение уравнения (2) в аналитической форме не представляется возможным. Поэтому для решения задачи применен метод конечных разностей.
На рис. 1 представлена расчетная область со схемой образования сеточных узлов. Для удобства организации вычислительного алгоритма принята неравномерная сетка, Δу = Δxtgβ. На каждом из характерных размеров расчетной области укладывается целое число узлов.
Уравнение (2) на трехточечном шаблоне аппроксимировано неявным консервативным конечно-разностным аналогом, решение которого осуществлено с применением метода разделения переменных и прогонки. Разработан вычислительный алгоритм, обладающий
устойчивостью и сходимостью.
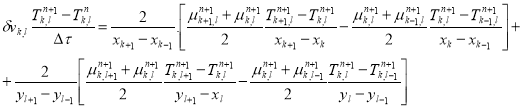 (9)
(9)
Граничные условия применительно к расчетной области: по внутрен-
нему контуру в соответствии с зависимостью (5), по внешнему контуру -
в соответствии с зависимостью (4). По линиям сопряжения принято условие (8). Особую проблему при решении задачи представляет формирование начальных условий (3). Проблема решена следующим образом. Принималось условие Т(х, y, 0) = (tвн + tнар)/2 и далее реализовывался вычислительный процесс для заданной закономерности изменения во времени параметров tнар и W6. Начиная с некоторого значения τ* на результаты вычисления Т(х, у, τ) значение Т(х,у,0) уже не оказывало влияния. Установлено, что применительно к решаемой задаче имеем условие τ* > 3 сут.
После каждого вычислительного цикла в соответствии с поступлением (стоком) теплоты корректировалось значение температуры внутреннего воздуха tвн.
Ряд ячеек пространственной сетки имеет отличающуюся конфигурацию (узлы A,B,C,D,E,F). Используя интегроинтерполяционный метод, для каждой из них составлено индивидуальное разностное уравнение (с учетом граничных условий). Например, для узла 6 уравнение имеет вид
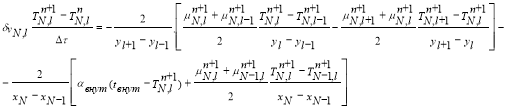 (10)
(10)
Разностные схемы (9), (10) аппроксимируют исходную задачу с погрешностью порядка 0 (![]() + hx2 + hу2). Суточные колебания температуры наружного воздуха влияют на распределение температуры на внутренних поверхностях и на температуру воздуха во внутренних объемах образцов БТВ. В этих условиях необходимо найти технические решения, которые могли бы предотвратить снижение температуры во внутренних объемах ниже температуры «точки росы» и уменьшить амплитуду колебания температуры поверхности расположенных во внутренних объемах технических объектов. Это может быть обеспечено при допустимом изменении температуры, прежде всего на внутренних поверхностях оболочки, которые и должны стать основным объектом исследований.
+ hx2 + hу2). Суточные колебания температуры наружного воздуха влияют на распределение температуры на внутренних поверхностях и на температуру воздуха во внутренних объемах образцов БТВ. В этих условиях необходимо найти технические решения, которые могли бы предотвратить снижение температуры во внутренних объемах ниже температуры «точки росы» и уменьшить амплитуду колебания температуры поверхности расположенных во внутренних объемах технических объектов. Это может быть обеспечено при допустимом изменении температуры, прежде всего на внутренних поверхностях оболочки, которые и должны стать основным объектом исследований.
Исследование закономерностей формирования температурного режима экспериментальным путем представляется достаточно затратным процессом — как с точки зрения затрат материальных ресурсов, так и затрат времени. Это показали проведенные эксперименты. По этой причине в данной работе эксперимент рассматривается в основном только как метод оценки адекватности аналитических решений реальным процессам формирования температурного режима.
Оценкой достоверности разработанной физико-математической модели является проверка ее адекватности, которая осуществлялась путем сравнения результатов расчетов на ЭВМ и экспериментальных данных при одинаковых температурных условиях.
При проведении натурного эксперимента и в ходе моделирования регистрировались следующие параметры: температура окружающего воздуха, температура некоторых точек внутри башни (A,B,C,D,E,F), относительная влажность, облачность. Для исключения влияния начальных условий на точность результатов, полученных при расчете на ЭВМ, показатели регистрировались после третьих суток.
В качестве меры совпадения результатов моделирования и натурных экспериментов выбиралась величина относительной погрешности 7-го регистрируемого параметра в k-м эксперименте
![]() (11)
(11)
где δi(k) — относительная погрешность 7-го регистрируемого параметра в k-м эксперименте, %; Yiэ — значение 7-го регистрируемого параметра, полученное в результате k-го натурного эксперимента; Yip — то же по результатам математического моделирования.
Средняя относительная погрешность 7-го регистрируемого параметра по совокупности экспериментов и расчетов на физико-математической модели определялась по формуле
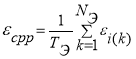 (12)
(12)
где δсрi — средняя относительная погрешность 7-го регистрируемого параметра по совокупности экспериментов и расчетов на физико-математической модели; N — число проведенных экспериментов.
Составленная на ЭВМ программа позволяет определять влияние окружающей среды на формирование тепловлажностного режима во внутреннем объеме образец объектов для всех периодов года при различных положениях относительно сторон света и мест хранения.
Заключение
Расчёт температурного и влажностного режима является основой для управления температуры и влажности внутри бронетанковой техники при длительном хранении. Далее проводить экспериментальные исследования для измерения параметров воздуха некоторых части внутри бронетанковой техники при длительном хранении. И оценки теоретических и экспериментальных исследований для формирования температуного и влажностного режима воздуха внутри бронетанковой техники (пример на танк Т-54, 55, 62 и БМП-1,2...) при длительном хранении в эксплуатационных условиях Вьетнама.
Литература:
- Руководство по хранению бронетанкового вооружения и техники.М.: Военное издательство, 1985.-296с.
- Исследование эффективности современных методов хранения и способов консервации новой автомобильной техники: тех. отчет Вч 63539, инв. № 874.-1977. -129с.
- Карташов, Э. М. Аналитическая теория теплопроводности и прикладной термоупругости: учеб. пособие / Э. М. Карташов. — М.: Либроком., 2012. — 656 с.
- Лыков, А. В. Теория теплопроводности: учеб. пособие / А. В. Лыков; под ред. Е. С. Гридасова. — М.: Высш. шк., 1967. — 600 с.

