Байесовская методология отличается от других подходов тем, что еще до получения данных исследователь определяет уровень своего доверия к возможным моделям и впоследствии представляет ее в виде определенных вероятностей. После того, как исследователем получены данные, с использованием теоремы Байеса он находит еще одно множество вероятностей, которые являются пересмотренными степенями доверия к возможным моделям с учетом полученной исследователем новой информации.
Ключевые слова: метод, анализ, прогнозирование, оценки, экономика, экономические процессы
The Bayesian methodology differs from other approaches in that, even before receiving the data, the researcher determines the level of his trust in possible models and subsequently presents it in the form of certain probabilities. After the researcher has obtained the data, using the Bayes theorem he finds another set of probabilities, which are revised degrees of confidence in the possible models, taking into account the new information received by the researcher.
Keywords: method, analysis, forecasting, estimation, economics, economic processes
Байесовские методы разработаны вследствие многочисленных попыток ученых определить проблемы статистического анализа поведения различных процессов и найти их решение с помощью применения основы байесовской методологии — теоремы Байеса. Использование данной теоремы имеет ряд предпосылок, основная из которых — наличие определенных соотношений между вероятностями явлений, имеющих различный характер и спецификации любого явления на нужном уровне [1].
Байесовская методология отличается от других подходов тем, что еще до получения данных исследователь определяет уровень своего доверия к возможным моделям и впоследствии представляет ее в виде определенных вероятностей. После того, как исследователем получены данные, с использованием теоремы Байеса он находит еще одно множество вероятностей, которые являются пересмотренными степенями доверия к возможным моделям с учетом полученной исследователем новой информации.
Одним из ключевых преимуществ байесовского подхода является использование любой начальной (априорной) информации относительно параметров модели. Такая информация выражается в виде априорной вероятности или функции плотности вероятности. Затем начальные вероятности «пересматриваются», с помощью выборочных данных, которые находят свое отображение в виде апостериорного распределения оценок параметров или переменных модели.
Необходимо выделить следующие особенности байесовского подхода:
‒ абсолютно все параметры и величины принято считать случайными, а именно точное значение параметров неизвестно исследователю, из чего следует то, что параметры являются случайными с точки зрения незнания исследователя;
‒ методы Байеса используются даже при нулевом объеме выборки. В этом случае значения априорного и апостериорного распределений равны;
‒ для оценки неизвестных переменных используют апостериорные распределения, то есть, найти решение задачи по оцениванию определенной величины, означает определить апостериорное распределение этой величины;
‒ основным инструментом подхода является формула (теорема) Байеса, а также такие правила, как sum -rule (если A1, …, Ak — взаимоисключающие события, то одно из них происходит всегда) и product — rule (любую совместную плотность всегда можно разбить на множители).
Наряду с вышеперечисленными достоинствами байесовской методологии необходимо выделить ее недостатки. Начиная с 1930 гг. байесовская парадигма довольно часто подвергалась резкой критике и практически не находила применения по следующим причинам:
‒ В байесовских методах предполагается, что априорное распределение известно до начала наблюдений и не предлагается конструктивных способов его выбора;
‒ Принятие решения при использовании байесовских методов в нетривиальных случаях требует колоссальных вычислительных затрат, связанных с численным интегрированием в многомерных пространствах;
‒ Фишером была показана оптимальность метода максимального правдоподобия, а следовательно — бессмысленность попыток придумать что-то лучшее.
На сегодняшний момент (начиная с 1990 гг.) ученые наблюдают возрождение методологии Байеса, методы которой оказались полезными для поиска решений многочисленных и достаточно серьезных вопросов и проблем в сфере машинного обучения и статистики.
Теорема Байеса: формула, применение
Формула (теорема) Байеса является одной из фундаментальных теорем теории вероятностей и позволяет установить вероятность определенного события А, если имеет место возникновение другого взаимозависимого с ним статистически события В. Говоря иначе, применение теоремы Байеса дает возможность исследователю наиболее точно пересчитать вероятность, учитывая как информацию, полученную им ранее, так и новые данные более поздних наблюдений. Байесовская теорема может быть получена из фундаментальных аксиом теории вероятностей, а именно из условной вероятности. Формуле Байеса присущи определенные особенности, главная из которых состоит в том, что для использования теоремы на практике необходимо значительное количество вычислений и расчетов, вследствие этого оценки байесовской парадигмы нашли активное применение только в период после революции, произошедшей в сфере сетевых и компьютерных технологий.
Перед формулированием байесовской теоремы вероятности, используемые в ней, подвергались многочисленным вероятностным интерпретациям. В одной из них устанавливался факт того, что вывод формулы зависит напрямую от использования особого подхода к статистическому анализу. При применении байесовской интерпретации вероятности теорема Байеса показывает, как степень личного доверия способна значительно меняться после определенного числа возникших событий. В этом состоят основные выводы Байеса, ставшие фундаментальными для байесовской статистики. Однако теорема нашла свое применение не только в байесовском анализе, но и активно используется в большом количестве иных расчетов.
Теорема Байеса получила свое название в честь её автора Томаса Байеса (1702–1761) — английского математика, первым предложившего применение сформулированной им теоремы для корректировки убеждений, опираясь на свежеполученную информацию [4].
Сущность байесовской парадигмы состоит в том, что при нахождении исследователем новой информации она дает основу для измерения вероятностей, которые обусловлены связанными между собой событиями. Формула Байеса имеет следующий вид [1]:
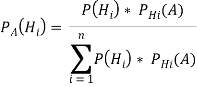 ,
,
где ![]() — вероятности гипотез до опыта (априорные вероятности);
— вероятности гипотез до опыта (априорные вероятности); ![]()
![]() — условные вероятности возникновения события А при выборе i-й гипотезы;
— условные вероятности возникновения события А при выборе i-й гипотезы; ![]() — условная вероятность i-й гипотезы после возникновения события А (апостериорная или послеопытная вероятность).
— условная вероятность i-й гипотезы после возникновения события А (апостериорная или послеопытная вероятность).
С помощью данной теоремы удается изменить значение вероятности на основе более поздних полученных сведений. Интерпретация байесовского подхода имеет следующий вид: пусть к началу реорганизации определенного объекта имеются n гипотез H1, H2, …, Hn о возможных его состояниях. На основе статистических данных за прошлые годы можно приписать им априорные вероятности P(H1), P(H2), …, P(Hn). Затем проводится эксперимент (реализуется проект), в результате которого может наступить или не наступить событие А. Опытным путем определяются условные вероятности возникновения события А при выборе i-й гипотезы ![]() как частоты наблюдения события А. При условии наступления события А делается переоценка веры в справедливость каждой гипотезы посредством замены вероятностей
как частоты наблюдения события А. При условии наступления события А делается переоценка веры в справедливость каждой гипотезы посредством замены вероятностей ![]() на вероятности
на вероятности ![]() .
.
Необходимо отметить, что в случае отсутствия статистических данных об априорных вероятностях наблюдений или гипотез о возникновении события А байесовскую методологию применить невозможно, так как подобная «формализация» теряет физический смысл [6].
Байесовская стратегия оценки достоверности выводов в экспертных системах
Байесовская стратегия оценки выводов находит все более частое применение в науке, экономике и промышленности. Для детального изучения байесовской стратегии необходимо рассмотреть пример оценки достоверности гипотезы на ее основе, а также обосновать использование теоремы Байеса для экспертных систем.
Для начала необходимо привести более расширенный вариант формулы Байеса с учетом некоторого события Е, связанного с событиями H1, H2,...,Hn. Вероятности события E известны при том условии, что какое-то из событий H1, H2,...,Hn наступило: P(E/H1), P(E/H2),..., P(E/Hn). Предположим, нам известно, что событие E произошло. В этом случае вероятность того, что какое-либо из событий Hi (i=1,...,n) наступило, определяется по следующей формуле [2]:
![]()
События H1, H2,...,Hn — гипотезы, а событие E называется свидетельством. Вероятности гипотез P(Hi) без учета свидетельства (т. е. без учета того, произошло событие E или нет) называются доопытными (априорными), а вероятности P(Hi/E) — послеопытными (апостериорными). Величина P(EHi) — совместная вероятность событий E и Hi, т. е. вероятность того, что произойдут оба события вместе. Величина P(E) — полная (безусловная) вероятность события E.
В экспертных системах (компьютерные системы, которые способны частично заменить специалиста-эксперта в разрешении конкретной проблемной ситуации) теорема Байеса может использоваться для оценки вероятностей заключений продукционных правил на основе данных о достоверности их посылок. Заключения (выводы) в этом случае соответствуют гипотезам в теореме Байеса, а посылки — свидетельствам. Обычно посылка правила в экспертных системах содержит несколько условий. Вероятности P(Hi) и P(E/Hi) определяются на основе статистических данных с использованием основных формул, применяющихся в теории вероятностей (формулы умножения вероятностей, формулы сложения вероятностей).
В качестве наглядного примера рассмотрим экспертную систему, которая помогает оценить условия труда рабочих в определенной организации. В следующей таблице представлены данные о 5 тыс. рабочих (у 315 обнаружено заболевание, возникшее в связи с их профессиональной деятельностью):
Таблица 1
Пример оценки достоверности гипотезы
|
Условие |
Значение |
Кол-во ситуаций обнаружения проф. заболеваний |
Кол-во рабочих, укоторых нет проф. заболевания |
|
Контакт с вредными веществами |
Постоянно Часто Периодически Отсутствует |
262 37 14 2 |
237 517 1011 2920 |
|
Физические нагрузки |
Большие Средние Нет |
168 111 36 |
927 1847 1911 |
|
Нервное напряжение |
Есть Нет |
202 113 |
1532 3153 |
|
Общие заболевания |
Есть Нет |
196 119 |
2011 2674 |
Источник: [2]
Необходимо дать оценку вероятности появления болезни у рабочего, работа которого почти каждый день связана с контактом с вредными веществами; также его деятельность связана с физическими нагрузками среднего уровня, нервное напряжение отсутствует, общих заболеваний у рабочего также нет.
В приведенной выше таблице за гипотезы берется уровень состояния здоровья рабочих: H1 — наличие профессиональной болезни, H2 — отсутствие профессиональной болезни.
За свидетельство принимается совокупность 4х факторов, описывающих работу: присутствие контакта с вредными для здоровья веществами, физические нагрузки, присутствие нервного напряжения, наличие общих заболеваний (свидетельства E1, E2, E3, E4). Совокупность всех 4х факторов принимается за событие E.
По формуле Байеса определим вероятности, которые нужны для дальнейших расчетов. Априорные вероятности гипотез (вероятности нахождения профессиональных заболеваний и их отсутствие без учета рабочих условий):
P(H1)=315/5000=0,063;
P(H2)=120/173=0,937.
Наблюдаемым свидетельством выступает совокупность 4х событий, которые наблюдаются совместно: частый контакт с вредными веществами, средний уровень физической нагрузки, отсутствие нервного напряжения и общих заболеваний. При условии, что эти события считаются независимыми, определяются условные вероятности свидетельства с помощью формулы произведения вероятностей:
P(E/Hi) = P(E1,E2,E3/Hi) = P(E1/Hi) P(E2/Hi) P(E3/Hi), i=1,2.
Затем определим величины, которые нужны для дальнейшего использования формулы произведения вероятностей:
P(E1/H1)=37/315=0,117;
P(E2/H1)=111/315=0,352;
P(E3/H1)=113/315=0,359;
P(E4/H1)=119/315=0,378;
P(E1/H2)=517/4685=0,11;
P(E2/H2)=1847/4685=0,394;
P(E3/H2)=3153/4685=0,673;
P(E4/H2)=2674/4685=0,571.
P(E1/H1) — вероятность того, что сотрудник часто контактирует с вредными веществами, при том условии, что в будущем у него будет обнаружено профессиональное заболевание. Данная величина отображает, с какой частотой у сотрудников, часто контактирующих с опасными веществами, находят профессиональное заболевание.
Подставив найденные величины в формулу произведения вероятностей, получаем: P(E/H1) = 0,117·0,352·0,359·0,378 = 0,006;
P(E/H2) = 0,11·0,394·0,673·0,571 = 0,017.
P(E/H1) — величина, показывающая вероятность рабочих условий при том условии, что в будущем у сотрудника обнаружат профессиональное заболевание.
Найдем апостериорную вероятность обнаружения профессионального заболевания при фактических рабочих условиях:
Полученная апостериорная вероятность выступает наиболее четкой оценкой вероятности обнаружения у сотрудника организации профессионального заболевания, чем априорная вероятность P(H1), которая была получена на основе данных без учета рабочих условий. Стоит заметить, что рассчитанная апостериорная вероятность (0,022) меньше, чем априорная вероятность (0,063). Из этого можно сделать вывод, что наблюдаемые свидетельства (частый контакт с вредными веществами, физическая нагрузка среднего уровня, отсутствие нервного напряжения и общих заболеваний) полностью подтверждают гипотезу, которая говорит о том, что профессиональное заболевание у сотрудника не появится.
Байесовское моделирование (метод байесовских сетей)
Понятием «байесовские сети» обозначают графические структуры, которые служат для представления вероятностных отношений между значительным числом переменных, а также структуры, необходимые для осуществления вероятностного вывода на основе представленных переменных [4].
Альтернативным названием метода байесовских сетей выступает понятие «байесовская классификация». Изначально байесовскую классификацию применяли для формализации экспертных знаний в экспертных системах. В настоящее время байесовская классификация используется также в качестве одного из методов Data Mining. Понятие «Data Mining» обозначает добычу данных, их глубинный анализ, также данное понятие применяется в целях обозначения системы методов нахождения в статистических данных неизвестных ранее, практически полезных знаний, нужных для принятия решений в различных областях деятельности людей.
В большей степени простым вариантом метода, использующего байесовскую классификацию, является «наивная» классификация или, иными словами, наивно-байесовский подход. С использованием данного подхода решаются задачи классификации. «Наивная» классификация является довольно легким для понимания методом классификации. Название «наивная» берет начало из предположения о том, что признаки являются взаимно независимыми. Следует выделить перечень основных свойств наивной классификации [5]:
- Использование всех переменных и нахождение абсолютно всех связей между ними.
- Относительно переменных существует два предположения:
‒ все переменные имеют одинаковую значимость;
‒ все переменные независимы статистически.
Следует выделить ряд преимуществ байесовских сетей:
‒ в модели устанавливаются связи между всеми переменными, что предоставляет возможность легко подвергать обработке случаи, где отсутствуют значения некоторых параметров;
‒ байесовские сети довольно легки в интерпретации и дают возможность при прогностическом моделировании проводить анализ по сценарию «что, если»;
‒ байесовский метод дает возможность совмещать закономерности, которые были выведены из статистических данных, и знания экспертов, которые были получены фактически;
‒ применение байесовских сетей на практике позволяет избежать чрезмерного усложнения модели.
Помимо перечисленных выше преимуществ, наивно-байесовский подход обладает такими недостатками, как [5]:
‒ перемножать условные вероятности корректно только тогда, когда все входные переменные действительно статистически независимы; хотя часто данный метод показывает достаточно хорошие результаты при несоблюдении условия статистической независимости, но теоретически такая ситуация должна обрабатываться более сложными методами, основанными на обучении байесовских сетей;
‒ невозможна непосредственная обработка непрерывных переменных — требуется их преобразование к интервальной шкале, чтобы атрибуты были дискретными; однако такие преобразования иногда могут приводить к потере значимых закономерностей;
‒ на результат классификации в наивно-байесовском подходе влияют только индивидуальные значения входных переменных, комбинированное влияние пар или троек значений разных атрибутов здесь не учитывается. Это могло бы улучшить качество классификационной модели с точки зрения ее прогнозирующей точности, однако, увеличило бы количество проверяемых вариантов.
Байесовская классификация нашла широкое применение на практике. Не так давно ее было предложено использовать для персональной фильтрации спама. Первый фильтр был создан Полем Грахемом. Для правильной работы алгоритма необходимо выполнение двух требований.
Первое требование — необходимо, чтобы классифицируемый объект обладал достаточным количеством признаков. Этому идеально удовлетворяют все слова писем пользователя, за исключением совсем коротких и редко встречающихся.
Второе требование — постоянное переобучение и пополнение набора «спам — не спам». Данные условия корректно работают в локальных почтовых клиентах, так как поток «не спама» у конечного клиента довольно постоянен, а если изменения присутствуют, то они не носят стремительного характера.
Однако для всех клиентов сервера точное определение потока «не спама» представляет значительную сложность, так как одно и то же письмо, выступающее для одного клиента спамом, для другого клиента спамом не является. Словарь получается слишком объемного размера, также не присутствует четкого разделения на спам и «не спам», вследствие этого качество классификации, в конкретном случае решение задачи фильтрации писем, значительно понижается.
Выбор байесовских сетей доверия в качестве экспертной системы по сравнению с другими направлениями их построения можно объяснить следующими причинами [7]:
‒ логический вывод в байесовских сетях доверия трактуется с точки зрения вычислений, так как теория, лежащая в основе вывода, имеет точное обоснование, отработанное за период, включающий в себя последние десятилетия. В то время, как системы, которые основаны на теории нечётких множеств, на теории функций доверия, а также теории Демпстера — Шефера, не имеют четкого обоснования с математической точки зрения и в многочисленных ситуациях используют эвристические процедуры (экспертные системы MYCIN, EMYCIN и т. п.)
‒ установлено, что психологически проще выполнять субъективное вероятностное оценивание причинно-следственных связей;
‒ теорию вероятности довольно часто подвергают критике с точки зрения её использования в «знаниях», однако, несмотря на это, она не нарушает общих представлений о «замкнутом мире» исследуемых объектов.
Одними из наиболее распространённых программных систем, реализующих теорию байесовских сетей доверия, являются «MSBN» фирмы Microsoft и «Hugin». Hugin является программой реализацией системы принятия решений на основе байесовских сетей доверия. Имеет две версии Pro и Explorer. Функционирует в среде OS Windows, а также имеет версию под UNIX. Эта система имеет развитый интерфейс и позволяет достаточно просто создавать базы знаний и фактов. Использует два основных режима работы:
‒ режим редактирования и построения причинно-следственной сети, а также заполнения таблиц условных вероятностей;
‒ режим расчёта вероятностных оценок для принятия решения по всем событиям, входящим в причинно-следственную сеть.
Расчёты могут осуществляться как на основе классической теории Байеса, так и на основе методов теории возможностей. «Hugin» имеет возможность связи с основными наиболее распространёнными программными средствами фирмы Microsoft. Данная ЭС имеет все основные функции любой информационной системы, включая такие как: хранение данных, вывод на принтер всех элементов ЭС, диагностика ошибок в работе.
Использование методологии Байеса в формировании статистических выводов дает возможность совсем по-иному воспринимать и исследовать оцениваемые модели. Он позволяет оперировать не только полученными оценками, а также соответствующими вероятностными распределениями, применять имеющиеся в разных формах априорные знания исследователя относительно оценок параметров модели. Это дает возможность получать большие объемы исходной информации и точнее описывать структуру и другие характеристики исследуемой модели.
Согласно приведенному в главе 3 примеру применения стратегии Байеса для оценки достоверности выводов можно утверждать, что при применении данной парадигмы могут быть получены результаты, которые учитывают влияние факторов различной природы.
Основными преимуществами рассмотренной в практическом примере стратегии выступают легкость обработки статистических данных, наличие возможности компьютерной реализации стратегии с минимальными затратами времени, возможность накопления и учета новых свежих знаний и данных, получения актуальных результатов, а также довольно хорошо известный математический аппарат.
Литература:
- Лопатников Л. И. Экономико-математический словарь: Словарь современной экономической науки. — 5-у изд., перераб. и доп. — М.: Дело, 2003. — 520 с.
- Моделирование процессов принятия решений в производственно-экономической системе / Макаров К. Г., Очкас М. В., Петренко В. Л., Ремпель А. Г.; Донец. гос. ун-т. — Донецк: ДонГУ, 1998. — 27 с.
- Недосекин А. О. Применение теории нечетких множеств к задачам управления финансами [Электронный ресурс] / А. О. Недосекин // Аудит и финансовый анализ. — 2000. — № 2. — Режим доступа: http://www. cfin.ru/press /afa/2000–2/08.shtml
- Фомин В. Н., Фрадков А. Л., Якубович В. А. Адаптивное управление динамическими объектами. — М.: Наука, 1981. — 184 с.
- Шапиро Л. Д. и др. Экономико-математическое моделирование / Л. Д. Шапиро, Г. В. Виноградов, Л. М. Лотош; Под ред. Л. Д. Шапиро; Том. гос. им. Куйбышева. — Томск: Изд-во Томск. ун-та, 1987. — 247 с.







