Исследование элементов троичной логики на примере троичного инвертора



Исследование элементов троичной логики на примере троичного инвертора

Султанов Иван Александрович, магистрант

Московский государственный технический университет имени Н. Э. Баумана

В статье представлены обзор, описание и исследование троичной логики, базовых троичных логических элементов на КМОП транзисторах, представлен обзор возможных троичных операций. В качестве примера троичного базового логического элемента рассмотрен троичный инвертор на КМОП транзисторах, его моделирование и испытание на практике. Даны рекомендации по разработке и проектированию базовых логических элементов троичной логики. Представлена топология троичного инвертора в кристалле.

Ключевые слова: троичная логика, КМОП, троичный инвертор, базовый логический элемент, топология

Trinary logic elements research on the example of trinary invertor

Sultanov I. A., master,

The article provides an overview, description and research of ternary logic, basic of ternary logic elements on the CMOS transistors, and provides an overview of the possible ternary operations. As an example, the base ternary considered ternary logic element inverter CMOS transistors, simulations and test it in practice. The recommendations on the development and design of the basic logic elements ternary logic. Presented ternary inverter topology on the crystal.

Keywords: ternary logic, CMOS, ternary inverter, basic logic element, topology

Современная двоичная электроника, особенно, двоичные ЭВМ, ушла далеко вперед и, в некоторых сферах, её развитие постепенно заходит в тупик. К примеру, малые топологические нормы, которые становятся приблизительно равными шагу кристаллической решетки кремния, а, отсюда, и малая ширина поликремниевого затвора КМОП транзистора, задают границу развития КМОП ИМС, так как при техпроцессе примерно равном шагу кристаллической решетки кремния, становится неизбежно влияние различных квантовых эффектов. Тот же закон Мура, также имеет свои границы, дальше которых перешагнуть, к сожалению, невозможно из-за влияния квантовых эффектов [1]. Остается только полностью поменять концепцию КМОП схем и ЭВМ на КМОП ИМС и предложить нечто совершенно новое.

Казалось бы, зачем кардинально все менять, если даже при техпроцессе 14 нм (FinFET) довольно многих все устраивает даже более чем? И ведь правда, большими частотами (единицы-десятки ГГц), количеством ядер (до 8-10) сейчас уже никого не удивишь, вся ответственность за быстродействие в большей степени перекладывается на программистов. А если нужны по-настоящему большие частоты (до терагерцового диапазона), то на помощь приходят полевые транзисторы с оптическим затвором, проводимость которых модулируется светом, либо же, чисто оптические транзисторы. Бытует мнение [2], что полевые транзисторы с оптическим затвором способны несколько сдвинуть границу закона Мура вверх.

Количество передаваемой информации за единицу времени можно также увеличить за счет увеличения разрядности, вместо частоты. Здесь на ум приходят квантовые ЭВМ [3], в которых каждый бит (кубит) может находиться в одном из двух состояний, подобно спину электрона [4]. Но проблема данного компьютера состоит в невозможности считать эту вероятность и оперировать ею: однажды считав кубит, он превращается в обычный бит и вся «квантовость» теряется. Также можно упомянуть биокомпьютеры, либо ДНК-компьютеры [5], но, к сожалению, эти виды ЭВМ, как и квантовые, не предназначены для решения широкого круга задач, а только каких-нибудь специфических (к примеру, кратчайший маршрут обхода вершин графа).

Но возможно ли поменять концепцию ЭВМ не используя различную экзотику, такую как квантовые, биокомпьютеры и оптические транзисторы, не теряя при этом всей функциональности современных ЭВМ? Действительно, у удобной, компактной и дешевой КМОП технологии нет аналогов. Она, как никакая другая, подходит для двоичных ЭВМ. Однако, разве на многоядерных, высокочастотных и технологичных двоичных ЭВМ на КМОП разве должно все заканчиваться? Возможно, это так, если потребности пользователей и программистов двоичной ЭВМ удовлетворены, и вся работа по достижению быстродействия лежит на разработчиках программ и ОС.

Однако, не дает покоя мысль о многозначных логиках [6]. Да, они сложнее, нежели двоичная (включил/выключил) и, возможно, не смогут обеспечить должного быстродействия и помехоустойчивости. Среди всех многозначных логик выделяется троичная логика, которая сохраняет в себе все свойства двоичной логики и добавляет новые [7, 8].

Чем так примечательна троичная логика и почему не выбрать, к примеру, четырехзначную или, вовсе, десятичную логику, где в каждом разряде передается куда большее количество информации? Ответ кроется в экономичности различных видов логик [9].

Экономичность характеризуется количеством информации, которое можно представить с помощью некоторого числа знаков n в данной логике. В свою очередь, n выражается через количество триггеров r(запоминающих ячеек), умноженное на число логических уровней данной логики p (основание)

(1)

Теперь попробуем представить какой диапазон значений m (количество информации) можно охватить, используя одинаковое число знаков n в различных видах логик. Для этого необходимо составить график функции при n = 8 (рисунок 1)

или (2)

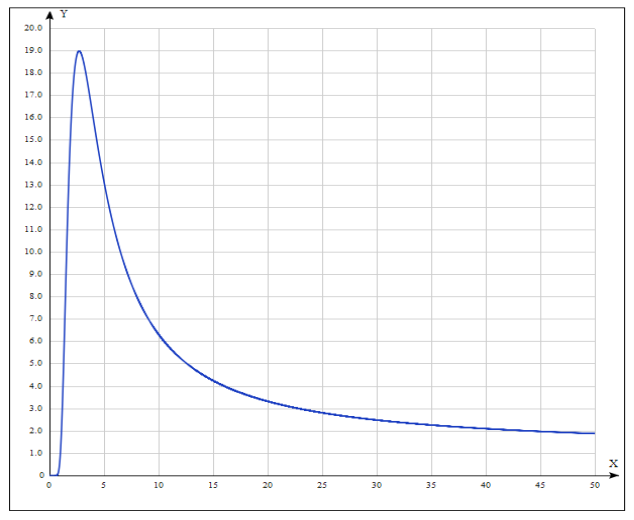
Рис. 1. Зависимость диапазона значений (Y) от основания логики (X) при одинаковом числе знаков n

Далее, попробуем найти экстремум функции . Для этого вычислим её производную

(3)

Следовательно, самой экономичной логикой с целочисленным основанием является троичная, так как 3 ближе к числу e. И, если взять основание, равное 4 и более, то, как видно из рисунка 1, при n = 8, к примеру, для четырехзначной логики (r = 2, p =4), мы сможем представить числа в диапазоне всего лишь от 0 до 15(либо от -8 до 7), а в случае троичной логики (p = 3, r ≈ 3) – в диапазоне от 0 до, примерно, 18 (или от -9 до 8). Для двоичной логики при n = 8 (r = 4, p = 2) диапазон чисел будет равен также от 0 до 16, как и в случае четырехзначной логики.

Преимущества троичной логики перед всеми возможными видами логик очевидны, но можно рассмотреть преимущество ещё на одном примере. Допустим, нам дано число 30, и надо его представить в двоичной, троичной и четырехзначной логиках. Для двоичной логики понадобится r = 5 триггеров, для троичной r = 4 триггера, для четырехзначной r = 3 триггера. Числа знаков, соответственно, будут равны 10, 12 и 12, а диапазоны значений при указанных количествах триггеров, соответственно, равны 0…31, 0…80 и 0…63. В этом примере примечательно то, что числа знаков у троичной и четырехзначной логик равны, но, количество информации, которое можно представить с помощью данного числа триггеров и количества логических уровней, у троичной логики выше, чем у четырехзначной. Иными словами, троичная логика является «золотой серединой» среди всех целочисленных логик при представлении некоторого числа минимальным набором триггеров и логических уровней. В четырехзначной логике и всех последующих триггеров хоть и меньше, но количество уровней приходится увеличивать, что ведет к снижению помехоустойчивости в разы.

Ещё одно достоинство троичной логики – это возможность симметрии. Иначе, в двоичной логике используются логические уровни 0, 1, в троичной несимметричной 0, 1, 2, а в симметричной -1, 0, +1 или -, 0 +. В четырехзначной логике используются уровни 0, 1, 2, 3, а ось симметрии появляется только в пятизначной логике (0, 1, 2, 3, 4) относительно числа 2, но уже значительно снижается помехоустойчивость из-за увеличения количества логических уровней.

Симметрия дает довольно значимое преимущество – это возможность безо всяких трудностей (вроде перевода в обратный и дополнительный коды, как в случае двоичной логики и иных несимметричных) представлять отрицательные числа и проводить различные операции над ними. К примеру, если взять число 10 в симметричной логике (+0+), то, для того чтобы получить -10, нам необходимо инвертировать все троичные разряды (триты) относительно 0. В итоге получаем -0-. При проведении операции суммирования, используя отрицательные числа, сумматор автоматически становится субстрактором (вычитателем). К примеру, 10 + (-10) = 0, что аналогично (+0+) + (-0-) = 000.

Ещё одно преимущество троичной логики кроется в представлении чисел с плавающей запятой, однако, в этом случае придется использовать несимметричную логику. Преимущество состоит в наилучшем округлении числа при отбрасывании разрядов после запятой. К примеру, даны числа с плавающей точкой в троичной логике 0.2222 и, аналогичное, в двоичной 0.1111. Числа после запятой будут равны, соответственно, 0.987 для троичной и 0.937 для двоичной. Если отбросить один разряд, то будем иметь 0.222 и 0.111, а погрешности относительно первоначальных числе будут, соответственно, равны 0.024 и 0.062. При 0.22 и 0.11 погрешности составят для троичного числа 0.098, а для двоичного уже 0.185. Таким образом, в случае троичной логики, погрешность при отбрасывании разрядов увеличивается не столь значительно. В случае двоичной логики приходится прибегать к различным дополнительным методам по округлению чисел.

Стоит отметить некоторую особенность в схемотехнике троичных логических элементов на КМОП транзисторах, которая будет рассмотрена далее. Троичные логические элементы используют в качестве входных и выходных сигналов используют дифференциальные пары сигналов. С одной стороны это преимущество (снижается влияние помех), с другой – некоторый недостаток (увеличение количества входов и выходов в 2 раза, либо увеличение металлизации на топологии).

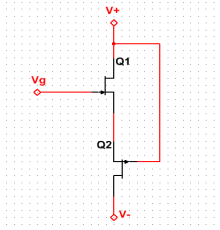
Рис. 2. NLT λ-транзистор

В некоторых источниках [8] предлагается использовать лямбда-транзистор (λ-транзистор) для построения троичных логических элементов, пример которого изображен на рисунке 2 (NLT λ-транзистор). Такой транзистор строится либо на полевых JFET транзисторах, либо на полевых транзисторах со встроенным каналом. Но, к сожалению, λ-транзистор не способен решить проблему энергопотребления логическим элементом, так как при нулевом напряжении на базе (логический 0), транзистор проводит довольно значительный ток.

Некоторые особенности троичной логики, возможно, ещё только предстоит узнать, так как она довольно плохо изучена в КМОП [8]. Однако, можно сказать наверняка, что троичная система счисления более характерна для повседневной жизни и различных реальных процессов, так как даже на любой заданный вопрос, иногда, невозможно однозначно ответить «да» (1) или «нет» (0), поэтому на помощь приходит троичная логика «да» (+ или 2), «нет» (- или 0) и «наверное» (или «не знаю», «неизвестно») (0 или 1). Можно привести несколько примеров доминирования только трёх состояний и не более:

− через 3 точки проходит только 1 плоскость (к примеру, табурет с тремя ножками намного устойчивее, чем с двумя);

− пространство, окружающее нас, имеет размерность 3, то есть, например, X(-), Y(0), Z(+);

− конденсатор заряжен либо положительно(+), либо отрицательно(-), либо вообще не заряжен(0);

− студент либо точно знает ответ на вопрос(+), либо точно не знает(-), либо неизвестно знает или нет(0).

И это далеко не все множество примеров троичной логики, перечислять их можно бесконечно.

Далее, будем исследовать троичную логику на практике путем построения и тестирования различных логических элементов.

1. История развития троичной логики.

Для начала, проведем краткий экскурс в историю развития троичной логики и троичных ЭВМ, которая была довольно короткой и неприметной:

− 1840 г., Томас Фоулер построил механическую троичную вычислительную машину (умножитель с 55-тритным регистром результата), одну из самых ранних механических вычислительных машин [12];

− 1947 г., после столетнего затишья, в работе [13], выполненной под руководством Джона фон Неймана, упоминается, но не обсуждается троичная система счисления;

− 1958 г., Н. П. Брусенцов построил в МГУ первую в мире опытную электронную троичную ЭВМ «Сетунь» [11] на ячейках из ферритдиодных магнитных усилителей переменного тока, работавших в двухбитном троичном коде (00 = 0, 01 = -, 10 = +, 11 = 0), четвёртое состояние двух битов не использовалось, либо принималось равным нулю. Для передачи данных по линиям использовалась однопроводная система, а для вычислений – двухпроводная [10]. Недостатком двухбитного троичного кода является различие результатов таких операций как троичное ИЛИ и троичное И, по сравнению с трехбитным (трехуровневым) троичным аналогом. В США, в то время, тоже рассматривали преимущества и недостатки троичного компьютера и после проведённых теоретических исследований строить троичный компьютер не стали;

− 1959 г., под руководством Н. П. Брусенцова разработана первая в мире серийная троичная ЭВМ «Сетунь». С 1962 г. по 1964 г. Казанским заводом математических машин было произведено 46 ЭВМ «Сетунь»;

− 1970 г., Н. П. Брусенцов построил в МГУ вторую электронную троичную ЭВМ «Сетунь-70»;

− 1973 г., Г. Фридер, А. Фонг и C. И. Чао, создали Ternac — экспериментальный троичный эмулятор;

− 2008 г., после более чем 30-летнего перерыва, Джефф Коннелли, Кираг Патель и Антонио Чавез, при поддержке профессора Филлипа Нико, построили трёхтритную цифровую компьютерную систему TCA2, версия 2.0 [14], в трёхуровневой однопроводной системе троичных логических элементов на 1484-х интегральных транзисторах. Однако, в данной ЭВМ используются те же двоичные КМОП транзисторы и проблема энергопотребления решается включением резисторов в стоки, что недопустимо, если речь заходит о большом быстродействии.

Больше никаких новшеств в области троичных ЭВМ не наблюдалось. Вообще, отношение к троичной логике наблюдается довольно скептическое, поскольку считается, что обычный транзистор может принимать только 2 логических состояния (открыт/закрыт), что не подходит для троичной логики, где предполагается третье промежуточное состояние. Однако, далее, мы попытаемся синтезировать элементарный троичный инвертор (основной элемент троичной логики) и показать, что не все так плохо, несмотря на то, что ни одного эффективного троичного логического элемента не было синтезировано в КМОП.

2. Элементы троичной логики и схемотехники.
   1. Синтезирование троичного инвертора и его сравнение с двоичным.

Троичный инвертор, как упоминалось ранее, является самым элементарным, наряду с троичным буфером [8]. Было решено строить инвертор исключительно в симметричной логике. Логический элемент КМОП будем синтезировать на основе существующего двоичного КМОП инвертора (рисунок 3). Из рисунка видно, что ток потребления при логическом 0 на входе составляет 62 мкА, что превышает в тысячи раз ток потребления в состояниях + и – (обычно 2-3 нА), поскольку транзисторы Q1 и Q2 при 0 на входе находятся в активном режиме (почти открыты оба) и пропускают некоторый, довольно большой, сквозной ток.

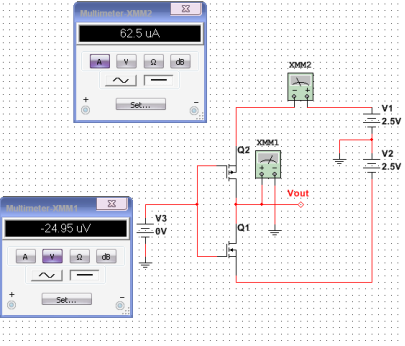
Рис. 3. Двоичный инвертор КМОП в симметричной троичной логике

Основной проблемой троичной логики на КМОП является создание логического элемента с почти нулевым (десятки-единицы наноампер) током потребления во всех состояниях (+,- и 0). Чтобы обеспечить минимальный ток, понадобится не 2 ключа (транзистора) как в двоичном случае, а 3 (рисунок 4). Vупр1, Vупр2 и Vупр3 являются управляющими напряжениями для ключей (для затворов транзисторов). В зависимости от входного сигнала Vвх, замыкается один из ключей, и на выходе Vвых появляется соответствующее напряжение. Таким образом, сквозные токи исключаются.

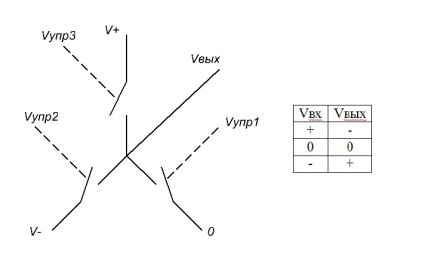
Рис. 4. Модель троичного инвертора КМОП и его таблица истинности

Следуя разработанной концепции троичного элемента, продолжим синтезирование его в КМОП. Для этого представим ключи на модели в виде транзисторов, стоки которых соединены в одной точке на выходе, а истоки подключены к соответствующим сигналам (рисунок 5). Здесь отпадает необходимость в Vупр1 и требуется схема управления для Vупр2 и Vупр3. Троичные сигналы показаны для каждого участка схемы.

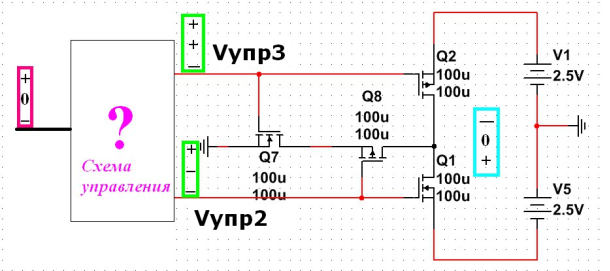
Рис. 5. Синтезированная схема троичного инвертора без схемы управления

Идеальной схемой управления послужил полевой транзистор, включенный по схеме с общим затвором (рисунок 6). Входной сигнал подается, непосредственно, на истоки транзисторов Q5 и Q6. Резисторы нагрузки R1 и R2 ухудшают значительно параметры логического элемента (либо увеличивается энергопотребление, либо снижается максимальная частота работы). Чтобы этого не допустить, необходимо заменить эти резисторы чем-нибудь.

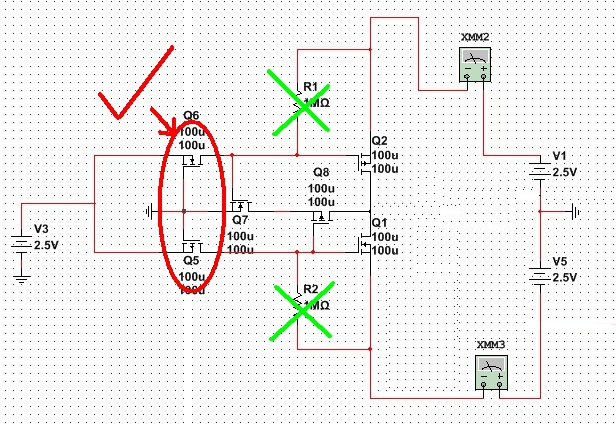
Рис. 6. Синтезированная схема троичного инвертора со схемой управления и резисторами нагрузки

Единственной верной заменой послужили КМОП транзисторы, включенные по схеме с общим истоком, лучшей замены не нашлось и, скорее всего, не найдется. Чтобы управлять этой комплементарной парой, необходим, к сожалению, дополнительный (вспомогательный) управляющий сигнал V2 (рисунок 7), который является противоположным входному инвертируемому сигналу V1 (информационному). Из рисунка можно заметить, что, теперь, при 0 на входе инвертор почти не потребляет тока от источника.

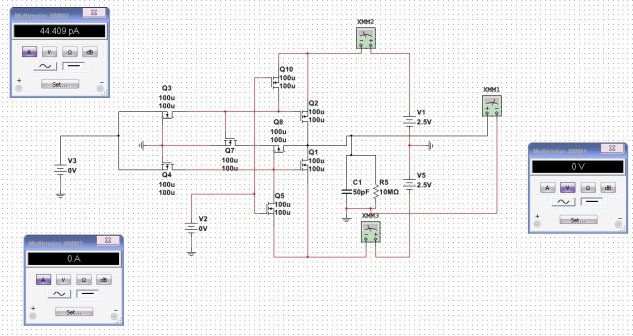
Рис. 7. Окончательно синтезированная схема троичного инвертора

Оценим работу инвертора в динамике. Для этого соединим последовательно 2 инвертора и подключим на вход, через резисторы, генератор троичного сигнала (рисунок 8). Осциллограммы входного и выходного сигналов изображены на рисунке 9. Выходной инвертор нагружен на емкость 10 пФ.

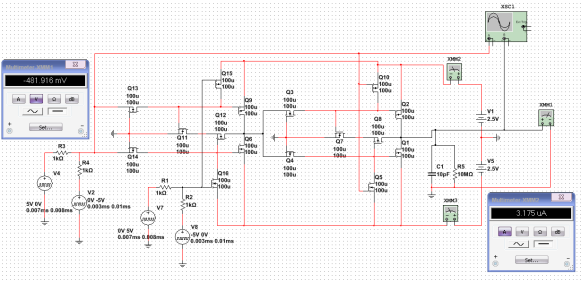
Рис. 8. Схема тестирования троичных инверторов в динамике

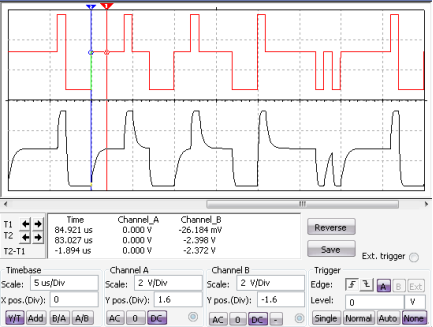
Рис. 9. Результаты тестов инвертора (красный – входной сигнал, черный – выходной)

Из результатов тестирования инвертора в динамике, можно с уверенностью сказать, что среднее значение потребляемого тока троичным инвертором теперь находится в пределах нормы и примерно равно току, потребляемому двоичным инвертором в динамике при одинаковой нагрузке (рисунок 10).

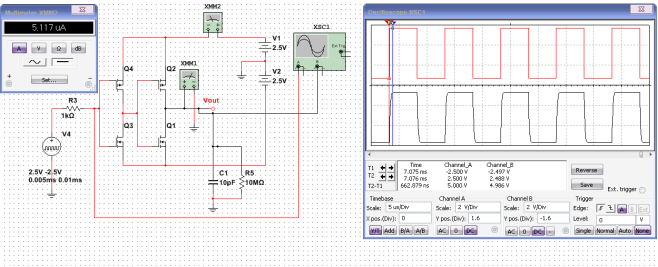
Рис. 10. Результаты аналогичных тестов для двоичного инвертора: (красный – входной сигнал, черный – выходной)

Сравнивая быстродействия логических элементов по передним и задним фронтам, приходим к выводу, что фронт двоичного инвертора на нагрузку 10 пФ длится около 500-600 нс, а фронт троичного, при переходе из - в 0 и из + в 0, при котором достигается наименьшее быстродействие, длится около 1-2 мкс. Следовательно, быстродействие троичного инвертора в 2-4 раза ниже, чем двоичного.

Ещё одним недостатком синтезированного троичного инвертора является низкое входное сопротивление со стороны информационного сигнала, но он устраняется с применением буфера-повторителя с низким выходным сопротивлением (к примеру, двухтактный повторитель). Однако, с применением полевых транзисторов с малым сопротивлением канала, такая необходимость отпадает.

Теперь, когда построен инвертор, то остальные базовые логические элементы троичной логики, такие как И и ИЛИ, синтезировать не составит труда.

Стоит отметить, что логические элементы построены на моделях почти идеальных КМОП транзисторов, характеристики которых сильно отличаются от реальных. Чтобы убедиться в полноценной работе троичного логического элемента, исследуем его на практике.

2.2. Исследование синтезированного троичного инвертора на практике и его сравнение с двоичным.

Практическое исследование троичного инвертора проводилось с использованием микросхемы IRF9952PBF (рисунок 11). Она содержит 2 КМОП транзистора в одном корпусе SOIC8 (p и n канальные КМОП). Питание было выбрано в диапазоне от 4 до 5 В (±2…2.5 В двуполярного). Генератор троичного сигнала с выходным сопротивлением 75 Ом был собран на микросхеме 74HC04. Частота троичного сигнала была выбрана равной 100 кГц.

Рис. 11. Макет троичного инвертора на IRF9952PBF

Дифференциальные входные сигналы IN+ (информационный) и IN- (вспомогательный, для вспомогательных транзисторов) показаны на рисунке 12. В отличие от тестов при моделировании, здесь испытывался инвертор на нагрузку 1 МОм, 20 пФ.

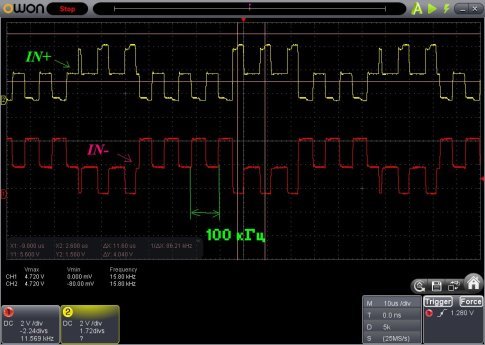
Рис. 12. Входные сигналы троичного инвертора

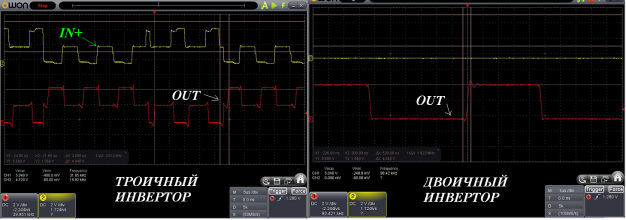
Рис. 13. Выходные сигналы троичного (слева) и двоичного (справа) инверторов на IRF9952PBF

Сравнивая выходные сигналы троичного инвертора (рисунок 13) и двоичного (рисунок 14), можно сделать вывод, исходя из длительностей фронтов, что быстродействие троичного варианта также в 2-4 раза меньше, чем двоичного (у троичного инвертора фронт длится максимум 2.3 мкс, а у двоичного 520 нс), как при моделировании.

При проведении всех практических испытаний, на осциллограммах были отмечены большие перерегулирования и иные переходные процессы, связанные с довольно большой затворной емкостью транзисторов микросхемы IRF9952PBF, которая колеблется в диапазоне 200…400 пФ, а также других паразитных явлений (например, большая длина монтажных проводников, индуктивность затворов и т. д.). Поэтому результаты эксперимента довольно преждевременны и различия в быстродействии могут быть даже в 2 раза меньше.

В целом, троичный инвертор не сильно уступает двоичному аналогу на практике. Недостатки имеются исключительно во входном сопротивлении, как было отмечено ранее, которое легко устранить схемно, и в меньшей помехоустойчивости, однако и этот недостаток устраняется с появлением дифференциальности входных сигналов. В крайнем случае, помехи, равные четверти полной шкалы питания, встречаются на практике довольно редко.

2.3. Возможное УГО троичного инвертора.

Теперь рассмотрим возможное графическое обозначение (УГО) троичного инвертора (рисунок 14).

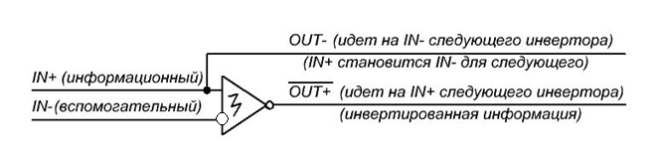Рис. 14. Возможное УГО троичного инвертора

Инвертор имеет дифференциальную пару сигналов IN+ и IN- (сигнал IN- является инверсией сигнала IN+). Сигнал IN- называется вспомогательным, так как не проходит, непосредственно, с входа инвертора на его выход, а управляет вспомогательными КМОП транзисторами, которые явились наиболее удачной заменой резисторам каскада общего затвора ранее, увеличивающей быстродействие логического элемента. Сигнал OUT+ является выходным сигналом, который представляет собой инвертированный входной информационный сигнал IN+. Сигнал OUT- представляет собой сигнал IN+, который служит сигналом IN- для следующего инвертора или другого логического элемента троичной логики.

На рисунке 15 а, б изображены различные возможные схемы включения троичных инверторов между собой.

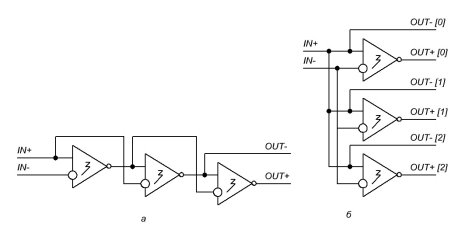
Рис. 14. Схемы включения троичных инверторов: а) последовательное включение; б) параллельное

Для того чтобы упростить чтение троичных принципиальных схем, можно использовать УГО инвертора на рисунке 15.

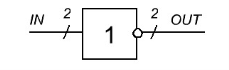
Рис. 15. Упрощенное УГО троичного инвертора

Подобное обозначение использовалось в двухбитных троичных схемах времен советской ЭВМ «Сетунь». Но может возникнуть путаница, так как в двухбитном троичном коде оба сигнала несут информацию, а в однотритном только один сигнал, другой является вспомогательным.

Заходя немного дальше, у других базовых троичных логических элементов (И, ИЛИ и т.д.) также будет по 2 входа и выхода на 1 троичный разряд.

3. Топология троичного инвертора в кремнии.

Напоследок, построим вариант топологии троичного инвертора в кремнии и оценим примерные размеры кристалла по сравнению с двоичным аналогом.

На рисунке 16а изображен вариант топологии троичного инвертора. Разводка слоев металлизации и поликремния, а также, расположение областей диффузий, возможно, выбраны не совсем удачно, но лучшего варианта, для меньшего объема занимаемой площади кристалла, найдено не было.

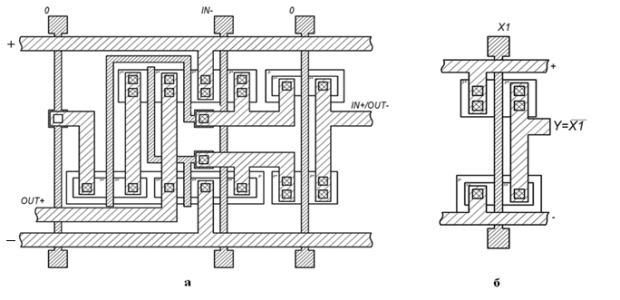
Рис. 16. Вариант топологии троичного инвертора (а) и топология двоичного (б) инвертора в кремнии

Глядя на топологию и сравнивая её с топологией двоичного инвертора (рисунок 16б), можно заметить, что общая площадь топологии троичного варианта в 3-4 раза больше двоичного. Для технологичности это является существенным недостатком. Также неудобна разводка шины 0 (общего провода), наряду с шинами + и – питания, и выходной шины. Возможно, для удобства разводки, придется производить какие-либо манипуляции с положением областей диффузий транзисторов.

Столько недостатков возникает в случае простейшего элемента логики – инвертора, а что будет, если сравнить двоичные и троичные топологии схем И и ИЛИ, представить страшно, но, с уверенностью можно сказать, что площадь также увеличится в 4 раза, но, возможно, даже в 5 из-за неудачной разводки.

Но стоит ли ставить точку на рассмотрении троичной схемотехники, которая обременена целой кучей технологических трудностей и иных недостатков? Однозначно нет. За все приходится чем-нибудь платить, но все это не напрасно.

4. Окончательное сравнение элементов троичной логики с двоичной.

Мы успели столкнуться с целой кучей недостатков троичных логических элементов перед двоичными, таких как схемотехническая сложность, увеличение и запутанность топологии, снижение рабочей частоты до 4 раз, наличие двуполярного питания, вместо простого однополярного, увеличение количества выводов при использовании дифференциальных пар сигналов и возможная худшая в 2 раза помехоустойчивость. Однако не стоит думать, что эти возможные недостатки полностью перечеркивают преимущества, которые оказываются, возможно, даже наиболее ценными. Таковых намечается пока только 2 для симметричной троичной логики: информационная емкость и представление чисел со знаками. Достоинства рассмотрим на конкретных примерах.

Возьмем для сравнения параллельную троичную и двоичную шины данных. Пусть их разрядность будет равна 4. Тогда диапазон передаваемых значений для троичной шины будет равен -40…40, а для двоичной 0…15. При одинаковой частоте шин информации будет передано в 5 раз больше в троичном случае без знака и в 2.5 раза больше для положительных чисел со знаком.

Теперь рассмотрим случай 10 разрядной параллельной шины. Размерность в 10 трит будем называть декатритом (5 трит – полудекатрит), по степеням десятки, так как единого стандарта «трайта» (по аналогии с двоичным байтом) до сих пор не существует. Но, стоит отметить, что Н. П. Брусенцов для ЭВМ «Сетунь» принял значение трайта, равным 6 трит.

Диапазон передаваемых значений станет равным для троичной шины -29524…29524, а для двоичной 0…1024. Не учитывая знак, количество информации в троичном случае будет передано в 57.6 раз больше, чем в двоичном, а со знаком, только для положительных чисел, в 28.8 раз.

С увеличением разрядности троичной шины, диапазон передаваемых значений будет расти экспоненциально по сравнению с двоичной.

Последовательная шина данных пока остается до конца не изученной, поскольку не совсем ясно как производить тактирование, по каким фронтам. Но, возможно, тактировать придется по двум передним фронтам троичного синхросигнала. Тогда, количество троичной информации также будет расти, по экспоненте по сравнению с двоичной, с увеличением количества переданных трит.

Как отмечалось ранее, троичные числа со знаком дают несомненное преимущество при проведении вычислительных операций, таких как суммирование, умножение и т.д. Не надо заботиться о знаке числа в старших разрядах и, тем самым, усложнять вычислительные схемы, как это делается в двоичной логике.

Единственным весомым недостатком является рабочая частота троичного элемента. Если, к примеру, тактировать сдвиговый регистр с частотой меньшей, хотя бы в 2 раза, чем частота двоичного синхросигнала, то, в этом случае, троичная логика проигрывает в разы и оказывается бесполезной. Однако, все зависит от конкретных задач. Тем более, на практике не удалось выяснить истинное быстродействие из-за различных паразитных явлений, возможно, оно не сильно отличается от быстродействия двоичного логического элемента, но медленнее (хотя бы в 2 раза) будет в любом случае, это факт.

Стоит, напоследок, отметить, что в троичной логике появляются многие новые операции, которых не было в двоичной, такие как модификация, операциявыбора, повторитель по совпадению (необходим для троичного полного сумматора), S-функция (или симметрия относительно нуля, необходима для троичного сумматора) и т. д. Все эти логические элементы будут, возможно, рассмотрены в следующих статьях.

Заключение.

В работе было проведено подробное исследование элементов троичной логики на примере троичного инвертора. Тем самым, получилось в некоторой степени сломать стереотип о бесполезности троичной логики и доказать, что довольно скептическое отношение к ней преждевременно.

Многие выявленные недостатки троичной логики, по сравнению с двоичной, могут быть легко компенсированы противодействующими факторами, а именно:

1) Малая помехоустойчивость. Однако, использование дифференциальной пары сигналов устраняет помехи по сигнальным линиям, повышая помехоустойчивость;

2) Увеличение количества входов и выходов в 2 раза. Однако информационная емкость увеличивается экспоненциально с ростом разрядности;

3) Увеличение сложности схемотехники. Но только на уровне базовых логических элементов. Дальше, скорее всего, должно быть намного проще. Хорошим примером может послужить троичный сумматор, который выполняет одновременно операции сложения и вычитания.

Единственными, на сегодняшний день, не решенными недостатками троичных схем остаются низкое быстродействие по сравнению с двоичными в 2-4 раза и рост топологии в 3-4 или даже в 3-5 раз. Если разрастание топологии в кристалле на первых порах более-менее решаемо технологически, то оценка быстродействия пока что преждевременна, хоть и была проведена на практике в данной статье, поскольку нужно проводить дополнительные исследования в этой области с использованием более сложных схем. Такими схемами могут служить последовательная шина данных и схемы на последовательностных тактируемых устройствах.

Не стоит забывать, что троичная логика – это та же двоичная, только с большими возможностями. Потенциал логики раскрыт далеко не полностью на сегодняшний день. И, кто знает, возможно, истина ближе, чем нам кажется.

Литература:

1. 10 летдо 10нм: законМуравсеещёработает // PCNews, 12.07.2008; Intel confident for 10nm and beyond 07/07/2008.

2. Световые транзисторы спасут закон Мура // N+1, 04.02.2016.

3. Ю. И. Манин. Вычислимое и невычислимое. // М.: Сов. радио, 1980. — С. 15.

4. Нильсен М., Чанг И. Квантовые вычисления и квантовая информация // Пер. с англ.— М.: Мир, 2006. 824 с.

5. ДНК-логика как основа биокомпьютера // Сергей Пахомов, КомпьютерПресс, 01.2007.

6. Карпенко А. С. Многозначные логики. Логика и компьютер // Вып. 4. М.: Наука, 1997. 223 с.

7. Карпенко А. С. Многозначные логики // Логика и компьютер. Вып. №4. — М.: Наука, 1997.

8. Кушнеров А. Троичная цифровая техника. Ретроспектива и современность // 28.10.05, Университет им. Бен-Гуриона Беэр-Шева, Израиль.

9. Экономичность систем счисления // trinary.ru, 12.12.09.

10. Бруснецов Н. П. Использование троичного кода и трехзначной логики в цифровых машинах // Научный отчет №24ВТ(378), МГУ, Москва 1969 г. 27 с.

11. Брусенцов Н. П., Маслов С. П., Розин В. П., Тишулина А. М. Малая цифровая вычислительная машина «Сетунь». // М.: Изд.МГУ, 1965.

12. The ternary calculating machine of Thomas Fowler // http://www.mortati.com/glusker/fowler/index.htm.

13. Jon von Neumann Preliminary Discussion of the Logical Design of an Electronic Computing Instrument // Institute of Advanced Study, 28 June 1946.

14. Ternary Computing Testbed 3-Trit Computer Architecture. Jeff Connelly // Computer Engineering Department, August 29th, 2008, with contributions from Chirag Patel and Antonio Chavez. Advised by Professor Phillip Nico. California Polytechnic.