Метрическая изменчивость и корреляция частей цветка некоторых видов семейства Бобовые



В статье раскрыты результаты исследования, связанного с изучением метрической изменчивостью корреляции частей некоторых видов семейства Бобовые.

Ключевые слова: растения семейства Бобовые, корреляция, метрическая изменчивость и корреляция частей цветка

Наличие функциональной и структурной взаимозависимости между структурами развивающегося организма, при котором изменения в одних органах приводят к изменениям в других, называется корреляцией, а связи между такими органами — коррелятивными.

Целостность организма предполагает согласованное изменение его органов и частей не только в онтогенезе (корреляция), но и в филогенезе. Сопряженное изменение органов в историческом развитии называется координациями [5].

Координации и корреляции связаны между собой, последние служат основой для первых. Корреляции касаются морфофизиологических взаимозависимостей формообразования в индивидуальном развитии, тогда как координации складываются исторически как приспособленная норма вида. Эволюция системы корреляции приводит к усилению целостности особи в историческом развитии [5].

Цветок покрытосеменных представляет собой один из самых популярных объектов ботанических исследований. Пожалуй, ни какому другому органу цветковых не уделяется столько внимания в литературе.

До сих пор остаётся актуальным вопрос изменчивости и соотношения различных частей цветка. Одни виды, чаще всего специфичные энтомофилы, обладают цветком с жесткой консервативной системой корреляций и координаций, другие (чаще всего неспецифичные энтомофилы и анемофилы) имеют цветок с более лабильной организацией. Картину запутывают многочисленные исключения из приведённой выше закономерности. Всё перечисленное и определяет актуальность нашей работы «Метрическая изменчивость и корреляция частей цветка некоторых видов семейства Бобовые».

Для использования параметрической статистики необходимо доказать, что признак подчиняется закону нормального распределения. Нами рассматривались 5 видов растений, у каждого из которых анализировалась изменчивость 8 признаков (длина и ширина весла, длина тычинок, длина пестика, длина и ширина паруса, длина и ширина лодочки) — то есть в общей сложности 45 признаков. Считаем, что не имеет смысла приводить в статье подробную проверку нормальности распределения всех признаков. Мы ограничимся лишь одним примером и сводной таблицей.

Рассмотрим в качестве примера проверку нормальности распределения длину пестика фасоли обыкновенной. В таблице 1 приведены расчёты важнейших показателей распределения – математического ожидания () и дисперсии (_x²).

Таблица 1

Расчёт математического ожидания () и дисперсии (_x²) распределения длины пестика фасоли обыкновенной

Интервалы (в мм)	Центры интервалов xi, (мм, λ=1)	Эмпирические частоты fi	Вероятность pi	xipi
12–13	12,5	5	0,025	0,313	4,603
13–14	13,5	7	0,035	0,473	3,802
14–15	14,5	22	0,110	1,595	5,371
15–16	15,5	44	0,220	3,410	2,378
16–17	16,5	49	0,245	4,043	0,110
17–18	17,5	52	0,260	4,550	6,175
18–19	18,5	19	0,095	1,758	8,240
19–20	19,5	2	0,010	0,195	1,953
Сумма		200	1	=16,335	= 32,632

Для дальнейшего доказательства нормальности распределения были рассчитаны средняя арифметическая и показатель среднего квадратического отклонения. Формально математическое ожидание соответствует средней величине эмпирического распределения, однако, по существу, эти показатели отождествлять нельзя [2]. Среднюю величину определяют как сумму всех членов ряда, отнесённую к их общему числу, а математическое ожидание представляет собой сумму произведений членов ряда на их вероятности. Эмпирическая средняя стремится к математическому ожиданию случайной величины по мере увеличения размера выборки; при небольшой выборке средняя может значительно отклоняться от своего математического ожидания [2].

Величина средней арифметической составила 16,301, что почти соответствует значению математического ожидания (16,335 — табл. 1) и связано это с достаточно большой выборкой — измерена длина 200 пестиков. На основе средней арифметической был рассчитан показатель среднего квадратического отклонения, который оказался равен 1,458. С использованием этих двух параметров мы рассчитали значения функции нормированного отклонения для каждого интервала распределения (табл. 2).

Таблица 2

Расчёт ординат нормальной кривой распределения длин пестика фасоли обыкновенной

Центры интервалов xi	Эмпирические частоты fi		Ординаты нормальной кривой f(t)
12,5	5	-2,606	0,0132
13,5	7	-1,920	0,0632
14,5	22	-1,235	0,1849
15,5	44	-0,549	0,3429
16,5	49	0,137	0,3951
17,5	52	0,823	0,2850
18,5	19	1,509	0,1276
19,5	2	2,195	0,0356
Сумма	200	-	-

Соответственно по значению функции нормированного отклонения (t) с использованием стандартной таблицы мы получили ординаты нормальной кривой f(t) и построить график распределения (рис. 1).

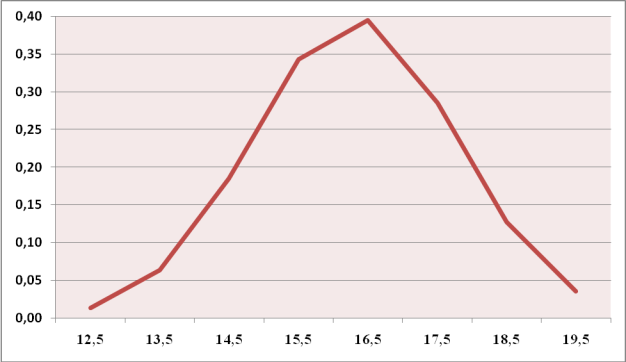
Рис. 1. Распределение показателей длины пестика фасоли обыкновенной по частотам встречаемости (по вероятности)

При сравнении крайних вариант (минимальной и максимальной длины пестика фасоли обыкновенной) с 3, оказалось, что х_min>-3 (12,06>11,96) и x_max<+3 (19,65<20,71), следовательно, наугад отобранная из всей совокупности варианта не отклониться от средней  более чем на t с вероятностью Р=0,9973. То есть 99,73% от всех вариант совокупности находятся в пределах 3, отсюда распределение признаётся нормальным.

В таблице 3 приведены сводные данные по проверки нормальности распределения всех признаков всех 5 видов растений.

Таблица 3

Проверка нормальности распределения промеров частей цветка исследуемых растений

Растение \ признак		хmin	xmax	интервал 3 ()
Лядвенец рогатый	Длина паруса	12,88	17,65	12,22–18,28
	Ширина паруса	7,56	14,80	7,24–15,16
	Длина весла	9,40	14,78	9,37–15,59
	Ширина весла	4,57	8,45	3,85–8,61
	Длина лодочки	7,93	14,02	7,90–14,07
	Ширина лодочки	3,14	6,45	3,04–6,55
	Длина пестика	10,69	17,79	10,68–17,86
	Длина тычинок	3,35	5,46	3,12–5,96
Горошек мышиный	Длина паруса	7,01	10,97	6,69–11,90
	Ширина паруса	2,85	8,88	1,69–9,28
	Длина весла	5,67	10,98	5,52–12,34
	Ширина весла	2,06	5,68	1,50–6,03
	Длина лодочки	6,77	9,67	5,18–10,16
	Ширина лодочки	2,36	6,94	1,01–6,77
	Длина пестика	5,31	9,93	3,57–11,23
	Длина тычинок	3,78	4,93	1,52–5,26
Фасоль обыкновенная	Длина паруса	12,03	15,87	11,48–16,70
	Ширина паруса	9,49	16,13	10,22–16,76
	Длина весла	13,36	20,57	13,33–21,39
	Ширина весла	5,96	10,93	5,86–12,01
	Длина лодочки	9,92	15,12	9,45–15,63
	Ширина лодочки	3,06	5,97	2,76–6,64
	Длина пестика	12,06	20,17	11,77–20,93
	Длина тычинок	6,59	9,97	6,07–10,00
Люпин многолистный	Длина паруса	12,56	18,83	11,51–20,08
	Ширина паруса	9,71	18,83	9,95–20,59
	Длина весла	11,25	18,09	10,48–19,09
	Ширина весла	6,74	13,68	6,91–14,72
	Длина лодочки	9,72	20,93	8,93–22,31
	Ширина лодочки	3,49	9,46	3,25–10,19
	Длина пестика	12,18	23,63	10,92–24,68
	Длина тычинок	6,89	12,72	5,98–12,74
Донник белый	Длина паруса	3,27	5,97	2,86–6,66
	Ширина паруса	2,17	5,80	1,04–5,81
	Длина весла	2,65	4,95	2,39–5,56
	Ширина весла	1,65	3,98	1,38–4,44
	Длина лодочки	2,41	4,92	2,40–5,17
	Ширина лодочки	1,97	3,81	1,65–3,82
	Длина пестика	2,58	5,03	2,53–5,42
	Длина тычинок	2,17	2,98	1,93–3,24

Как видно из таблицы, крайние варианты расположены в пределах3().То есть все анализируемые промеры всех 5-ти видов подчиняются закону нормального распределения.

В таблице 4 приведены показатели изменчивости промеров цветка исследуемых растений: средняя арифметическая и ее ошибка (±т_х), среднее квадратическое отклонение и его ошибка (S±m_s), коэффициент вариации и его ошибка (V ±m_v), показатель асимметрии и его ошибка (А±т_а) [1- 4].

Таблица 4

Показатели метрической изменчивости цветка исследуемых растений (во всех выборках n=200)

Лядвенец рогатый (Lоtus corniculаtus)
Длина паруса	15,25±0,07	1,01±0,05	6,64±0,33	-0,33±0,17
Ширина паруса	11,20±0,09	1,32±0,07	11,77±0,59	-0,14±0,17
Длина весла	12,48±0,07	1,04±0,05	8,30±0,41	-0,63±0,17
Ширина весла	6,23±0,06	0,79±0,04	12,75±0,64	0,17±0,17
Длина лодочки	10,98±0,07	1,03±0,05	9,36±0,47	-1,02±0,17
Ширина лодочки	4,80±0,04	0,59±0,03	12,20±0,61	0,99±0,17
Длина пестика	14,27±0,08	1,20±0,06	8,38±0,42	-1,06±0,17
Длина тычинок	4,54±0,03	0,47±0,02	10,46±0,52	-0,34±0,17
Горошек мышиный (Vícia crаcca)
Длина паруса	9,29±0,06	0,87±0,04	9,34±0,47	-0,25±0,17
Ширина паруса	5,49±0,09	1,26±0,06	23,04±1,15	0,83±0,17
Длина весла	8,93±0,08	1,14±0,06	12,71±0,64	-0,74±0,17
Ширина весла	3,77±0,05	0,76±0,04	20,08±1,00	0,03±0,17
Длина лодочки	7,67±0,06	0,83±0,04	10,82±0,54	0,12±0,17
Ширина лодочки	3,89±0,07	0,96±0,05	24,64±1,23	0,82±0,17
Длина пестика	7,40±0,09	1,28±0,06	17,25±0,86	-0,40±0,17
Длина тычинок	3,39±0,04	0,62±0,03	18,38±0,92	5,61±0,17
Фасоль обыкновенная (Phaseolusvulgaris)
Длина паруса	14,09±0,06	0,87±0,04	6,17±0,31	-0,23±0,17
Ширина паруса	13,49±0,08	1,09±0,05	8,08±0,40	-0,33±0,17
Длина весла	17,36±0,09	1,34±0,07	7,73±0,39	-0,22±0,17
Ширина весла	8,94±0,07	1,02±0,05	11,46±0,57	-0,78±0,17
Длина лодочки	12,54±0,07	1,03±0,05	8,21±0,41	0,28±0,17
Ширина лодочки	4,70±0,05	0,65±0,03	13,75±0,69	-0,14±0,17
Длина пестика	16,35±0,11	1,53±0,08	9,34±0,47	-0,18±0,17
Длина тычинок	8,03±0,05	0,66±0,03	8,15±0,41	0,51±0,17
Люпин многолистный (Lupínus polyphyllus)
Длина паруса	15,80±0,10	1,43±0,07	9,05±0,45	-0,10±0,17
Ширина паруса	15,27±0,13	1,77±0,09	11,61±0,58	-0,80±0,17
Длина весла	14,79±0,10	1,43±0,07	9,70±0,49	-0,01±0,17
Ширина весла	10,81±0,09	1,30±0,07	12,04±0,60	-0,84±0,17
Длина лодочки	15,62±0,16	2,23±0,11	14,28±0,71	-0,25±0,17
Ширина лодочки	6,72±0,08	1,16±0,06	17,20±0,86	-0,14±0,17
Длина пестика	17,80±0,16	2,29±0,11	12,89±0,64	0,12±0,17
Длина тычинок	9,36±0,08	1,13±0,06	12,02±0,60	-0,05±0,17
Донник белый (Melilotusalbus)
Длина паруса	4,76±0,04	0,63±0,03	13,32±0,67	0,02±0,17
Ширина паруса	3,43±0,06	0,79±0,04	23,19±1,16	1,68±0,17
Длина весла	3,98±0,04	0,53±0,03	13,31±0,67	-0,13±0,17
Ширина весла	2,91±0,04	0,51±0,03	17,51±0,88	0,39±0,17
Длина лодочки	3,78±0,03	0,46±0,02	12,21±0,61	-0,17±0,17
Ширина лодочки	2,73±0,03	0,36±0,02	13,18±0,66	0,88±0,17
Длина пестика	3,97±0,03	0,48±0,02	12,11±0,61	0,06±0,17
Длина тычинок	2,58±0,02	0,22±0,01	8,39±0,42	0,06±0,17

Видовая специфика и не столь близкое родство (сравниваемые виды относятся к разным родам), а также различные размеры цветков делают некорректным обобщённое межвидовое сравнение размерных характеристик цветков исследуемых растений по таким параметрам как, например, средняя изменчивость длины тычинок и средняя изменчивость длины пестиков всех растений. Поэтому мы будем сравнивать внутривидовые показатели изменчивости и отдельные (а не усреднённые) межвидовые характеристики.

Мы не станем акцентировать внимание на размерных характеристиках, описываемых средней арифметической, а также на среднем квадратическом отклонении, так как эти параметры использовались при проверке на нормальность распределения вариант. Кроме того, значения средней арифметической подтверждают очевидные факты (например, длина лепестков больше ширины; цветок лядвенца рогатого больше цветка донника белого и т. д.).

Гораздо больший интерес представляют значения коэффициентов вариации и асимметрии.

Длина паруса. Самыми консервативным парусом по максимальной длине обладают фасоль обыкновенная - Сm_c=6,170,31 и лядвенец рогатый - Сm_c=6,640,33 (табл. 4, рис. 8). Причём эти значения коэффициента вариации оказались минимальными среди всех сравниваемых промеров всех анализируемых растений. У мышиного горошка (Сm_c=9,340,47) и люпина многолистного (Сm_c=9,050,45) этот показатель более изменчив (табл. 4, рис. 2). Наибольшей изменчивостью длины паруса характеризуется донник белый (Сm_c=13,320,67).

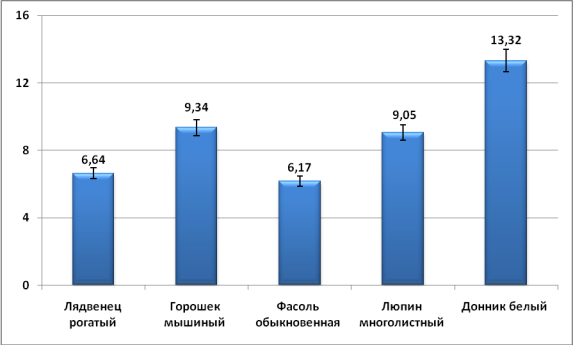
Рис. 2. Значение коэффициента вариации (Сm_c) длины паруса

Ширина паруса. По значению этого показателя отмечено одни из самых больших вариаций рассматриваемых признаков (табл. 4, рис. 9). У горошка мышиного и донника белого значение коэффициента вариации превысило 23 (Сm_c=23,04,15 и Сm_c=23,19,16 соответственно). У лядвенца рогатого и люпина многолетнего значение этого показателя оказалось чуть выше 11 (Сm_c=11,77,59 и Сm_c=11,61,58 соответственно). Наконец у обыкновенной фасоли значение коэффициента оказалось самым низким – Сm_c=8,080,40 (табл. 4, рис. 3).

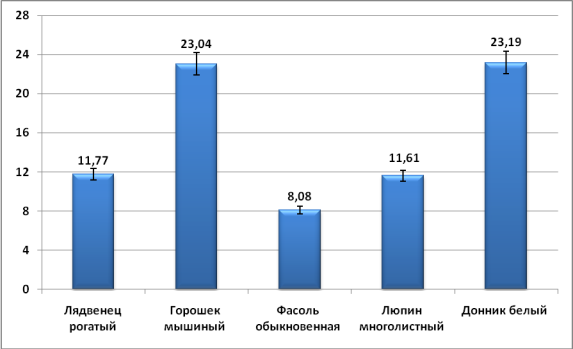
Рис. 3. Значение коэффициента вариации (Сm_c) ширины паруса

Длина весла. Наиболее изменчивыми по длине весла оказались цветки донника белого (Сm_c=13,310,67) и горошка мышиного (Сm_c=30,8540,908) (табл. 4, рис. 4).

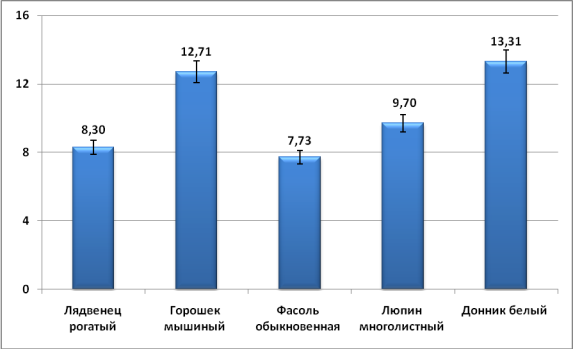
Рис. 4. Значение коэффициента вариации (Сm_c) длины весла

Наиболее консервативной длинной тычинок обладает фасоль обыкновенная — Сm_c=7,730,39. У лядвенца рогатого и люпина многолистного значение этого показателя несколько выше по сравнению с фасолью: (Сm_c=7, 730,39 и Сm_c=9,700,49 (табл. 4, рис. 10).

Ширина весла. По предыдущим промерам самым изменчивымцветком обладал донник белый. По ширине весла мышиный горошек (Сm_c=20,081,00) оказался более изменчивым, чем донник белый (Сm_c=17,510,88). Коэффициент вариации этого промера оставшихся видов изменяется в пределах от 11,46 до 12,75 (табл. 4, рис. 5).

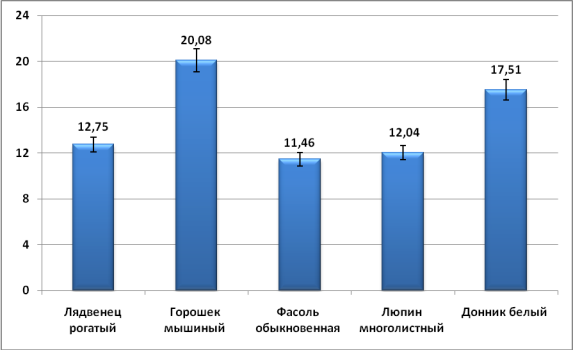
Рис. 5. Значение коэффициента вариации (Сm_c) ширины весла

Длина лодочки. Самой изменчивой длиной лодочкиобладает люпин многолистный(Сm_c=14,280,71), цветки которого по рассматриваем выше промерам обладают средними показателями изменчивости (табл. 4, рис. 6). Фасоль обыкновенная обладает самыми консервативными размерами цветка и по этому промеру (Сm_c=8,210,41), как и по анализируемым выше размерным характеристикам. Показатель изменчивости длины лодочки остальных растений занимает промежуточное положение, изменяясь в пределах от 9,36 (лядвенец рогатый) до 12,21 (донник белый).

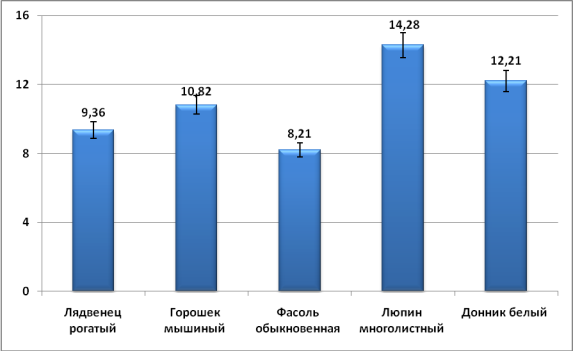
Рис. 6. Значение коэффициента вариации (Сm_c) длины лодочки

Ширина лодочки. Мышиный горошек обладает наибольшей изменчивостью этого промера (Сm_c=24,64,23), причём в этом случае значение коэффициента вариации оказалось наибольшим среди всех сравниваемых признаков (табл. 4, рис. 7).

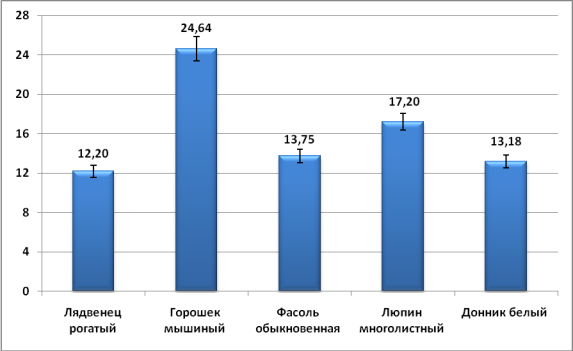
Рис. 7. Значение коэффициента вариации (Сm_c) ширины лодочки

По этому показателю впервые в анализе полученных результатов фасоль обыкновенная демонстрирует не самый низкий уровень изменчивости промера (Сm_c=13,750,69), превышая уровень изменчивости ширины лодочки лядвенца рогатого (Сm_c=12,200,61) и донника белого (Сm_c=13,180,66). Люпин многолистный обладает довольно высоким показателем изменчивости ширины лодочки - Сm_c=17,200,86.

Длина пестика. Показатели изменчивости длины пестика положительно коррелируют с показателями изменчивости ширины лодочки: самая разнообразная длина пестика у горошка мышиного (Сm_c=17,250,86); на втором месте располагается люпин многолистный (Сm_c=12,890,64); за ним следует донник белый (Сm_c=12,110,61) и фасоль обыкновенная (Сm_c=9,340,47), длины пестиков которых оказались изменчивее, чем у лядвенца рогатого (Сm_c=8,380,42) (табл.4, рис. 8).

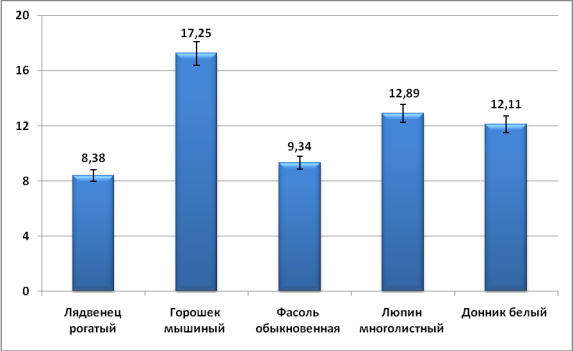
Рис. 8. Значение коэффициента вариации (Сm_c) длины пестика

Длина тычинок. По последнему анализируемому промеру, анализируя степень изменчивости, лидирует горошек мышиный, обладающий самыми разнообразными вариантами длины тычинок (Сm_c=18,380,92) (табл. 4, рис. 9). С большим отрывом он горошка отстаёт люпин многолистный (Сm_c=12,020,60) и лядвенец рогатый (Сm_c=12,200,61). Наименьшей изменчивостью этого признака обладают донник белый (Сm_c=8,390,42) и фасоль обыкновенная (Сm_c=8,150,41).

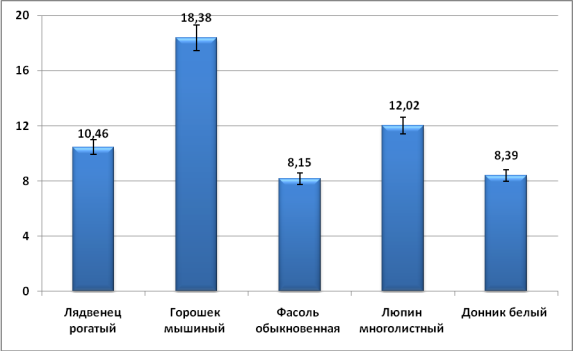
Рис. 9. Значение коэффициента вариации (Сm_c) длины тычинок

По отдельным признакам сложно судить об общей изменчивости цветка вида, поэтому мы рассчитали среднее значение коэффициента вариации (табл. 5, рис. 10).

Таблица 5

Среднее значение коэффициента вариации (С_ср) размеров частей цветка исследуемых растений

Вид	Сср
Лядвенец рогатый	9,98
Горошек мышиный	17,03
Фасоль обыкновенная	9,11
Люпин многолистный	12,35
Донник белый	14,15

Оказалось, что самым консервативным цветком обладает фасоль обыкновенная (среднее значение коэффициента вариации С_ср=9,11 (табл. 5, рис. 10)). Чуть более изменчивыми оказались цветки лядвенца рогатого — С_ср=9,98. Самым изменчивым по размерным характеристикам оказался цветок горошка мышиного С_ср=17,03. Цветки донника белого и люпина многолистного обладают промежуточным значением усреднённого коэффициента вариации (С_ср=14,15 и С_ср=12,35 соответственно).

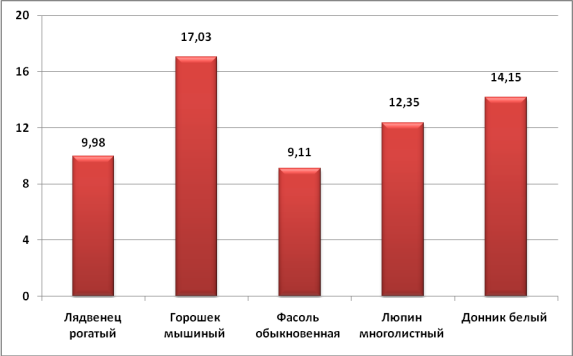
Рис. 10. Среднее значение коэффициента вариации (С_ср) размеров частей цветка исследуемых растений

Анализируя показатель асимметрии, можно заметить, что подавляющее большинство промеров характеризуются весьма невысоким значением коэффициента асимметрии, который во многих случаях даже не выходит за пределы ошибки, оставаясь в интервале от -0,17 до 0,17 (табл. 4, рис. 12). В подавляющем большинстве случаев наблюдается весьма незначительное смещение нормального распределения, при котором значение коэффициента асимметрии по модулю ниже 1 (|A|<1) (рис. 12). Наблюдаемая картина является доказательством действия стабилизирующей формы естественного отбора. Лишь в четырёх случаях значение коэффициента асимметрии является довольно весомой величиной, превышающей 1 по модулю: длины лодочки (А±m_а= –1,02±0,17) и пестика (А±m_а= –1,06±0,17) у лядвенца рогатого; ширина паруса донника белого (А±m_а=1,68±0,17) и самое высокое значение этого показателя — длина тычинок у мышиного горошка (А±m_а=5,61±0,17). В перечисленных случаях смещение нормального распределения является довольно существенным. Что же касается направления смещения, то 16 (40 %) промеров характеризуются положительным значением коэффициента асимметрии и смещением нормального распределения в сторону увеличения выраженности признака, тогда как 24 (60 %) признаков характеризуются отрицательным значением коэффициента асимметрии и смещением нормального распределения в сторону уменьшения выраженности признака (рис.11).

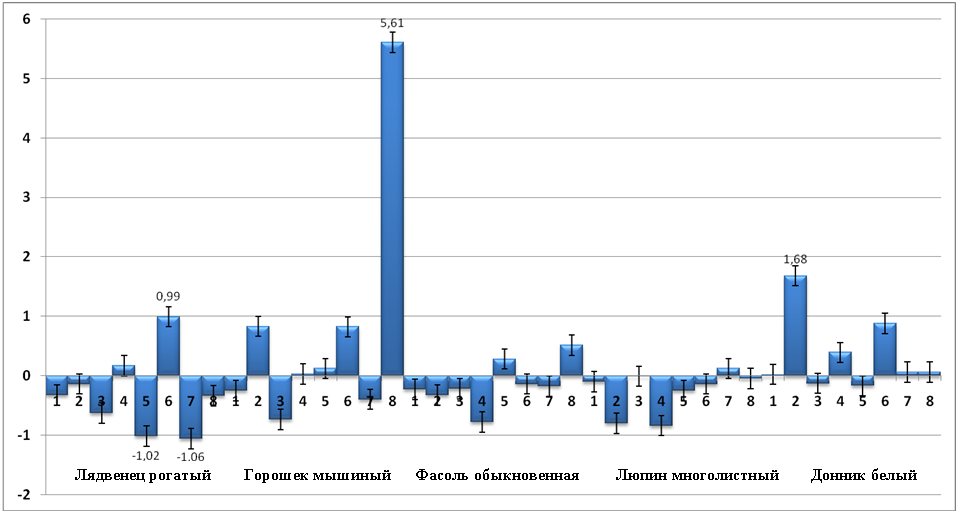
Рис. 11. Значение коэффициента асимметрии (А±mа) промеров исследуемых растений (1 - длина паруса; 2 - ширина паруса; 3 - длина весла; 4 - ширина весла; 5 - длина лодочки; 6 - ширина лодочки; 7 - длина пестика; 8 - длина тычинок)

Проведенное исследование позволило сформулировать следующие выводы:

1. Все анализируемые промеры цветков исследуемых растений подчиняются закону нормального распределения;
2. Самым консервативным цветком обладает фасоль обыкновенная (С_ср=9,11), несколько более изменчивыми оказались цветки лядвенца рогатого (С_ср=9,98). Самым изменчивым по размерным характеристикам оказался цветок горошка мышиного (С_ср=17,03). Цветки донника белого и люпина многолистного обладают промежуточным значением усреднённого коэффициента вариации (С_ср=14,15 и С_ср=12,35 соответственно);
3. Большинство промеров характеризуются невысоким значением коэффициента асимметрии (|A|<1), который во многих случаях не выходит за пределы ошибки, что определяется действием стабилизирующей формы отбора;
4. Наибольшее статистически достоверное значение коэффициента корреляции наблюдается у горошка мышиного при сравнении размеров длинных и коротких тычинок — |r|=0,751. Наименьшая величина коэффициента характеризует сопряжение длины тычинок и ширины паруса у донника белого |r|=0,139.

5. Наиболее жестко коррелированным цветком обладают люпин многолистный |r|_ср=0,365 и горошек мышиный |r|_ср=0,347, за ними следуют лядвенец рогатый |r|_ср=0,295 и донник белый |r|_ср=0,282. Цветком, менее всего связанным корреляционными связями, обладает фасоль обыкновенная |r|_ср=0,264.

Литература:

1. Животовский Л. А. Популяционная биометрия / Л. А. Животовский. — М.: Наука, 1991. — 271 с.
2. Лакин, Г. Ф. Биометрия / Г. Ф. Лакин. — М.: Высшая школа, 1990. — 352
3. Плохинский Н. А. Биометрия / Н. А. Плохинский. — М.: МГУ, 1970. — 367 с.
4. Рокицкий П. Ф. Биологическая статистика / П. Ф. Рокицкий. — Минск: Высшая школа, 1964. — 327 с
5. Яблоков, А. В. Эволюционное учение / А. В. Яблоков, А. Г. Юсуфов. — 6-е изд., испр. — М.: Высш. шк., 2006. — 310 с.