В процессе заготовки древесины при рубках ухода большое значение имеет процесс перемещения хлыстов и сортиментов от места валки до лесопогрузочного пункта.
Для этих целей в лесостепной зоне ЦЧР широко применяются бесчокерные трелевочные устройства, типа “Муравей” в агрегате с колесными сельско-хозяйствеными тракторами.
В процессе трелевки возникают большие динамические нагрузки, вследствие движения трактора по неровностям рельефа, и колебания трелюемой пачки. Динамические нагрузки воздействуют на навесную систему трактора и металлоконструкцию захватного устройства, что ведет к снижению надежности и производительности работы агрегата.
Одним из вариантов повышение эффективности работы и увеличения производительности трелевочных захватных устройств является применение рекуперативного гидропривода. Его использование возможно в машинах циклического действия: машины лесного комплекса, манипуляторы, краны, экскаваторы. Так в конструкции некоторых экскаваторов применена рекуперация энергии посредством пневмогидравлического аккумулятора [1], интерес также представляет почвообрабатывающий агрегат с тремя системами рекуперации энергии работающими независимо друг от друга [2].
Гидросистемы сельскохозяйственных тракторов не приспособлены для выполнения рабочих процессов трелевки в транспортном положении навесной системы, поэтому нами предлагается в гидросистему трактора подключить гидроаккумулятор, для снижения динамических нагрузок и рекуперации энергии.
С целью более полного и объективного представления процессов, происходящих в гидроприводе трактора во время трелевки, необходимо математически смоделировать динамику гидропривода навесной системы колесного трактора с захватом с применением гидроаккумулятора.
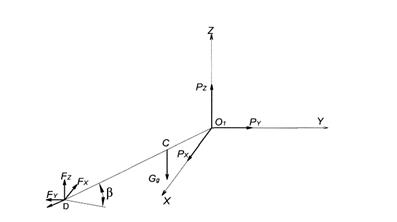
Сбор деревьев захватом производится путем перемещения дерева поднятого за один (комлевой или вершинный) конец. В этом случае на верхнюю часть пачки хлыстов действуют технологические силы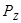 ,
, 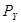 и
и 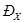 , а на нижнюю волочащуюся часть силы сопротивления волочению части дерева, лежащего на земле
, а на нижнюю волочащуюся часть силы сопротивления волочению части дерева, лежащего на земле 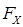 ,
,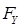 и
и 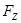 (рисунок 1).
(рисунок 1).
Используя материал представленный в [3] можно получить дифференциальное уравнение движения точки 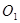 в пространстве в плоскости УОZ по прямой Z=КУ, где k=
в пространстве в плоскости УОZ по прямой Z=КУ, где k=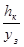
|
|
Рисунок 1 - Расчётная схема подъёма и перемещения дерева бесчокерным захватом
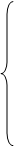 m
m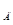
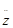
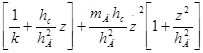 =P
=P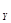 -F
-F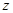
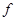
m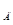
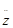
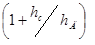 =P
=P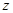 +F
+F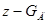
 (1)
(1)
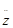
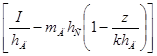 +
+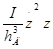 =G
=G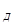 h
h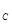 - F
- F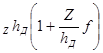
где h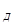 - длина захваченного дерева; h
- длина захваченного дерева; h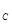 - расстояние от точки захвата до центра масс дерева; z - траектория движения дерева во время захвата и подтаскивания;
- расстояние от точки захвата до центра масс дерева; z - траектория движения дерева во время захвата и подтаскивания; 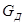 - сила тяжести захваченного дерева; m
- сила тяжести захваченного дерева; m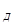 - масса дерева; h
- масса дерева; h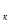 - высота подъёма захваченного дерева;
- высота подъёма захваченного дерева; 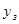 - горизонтальная координата перемещения центра тяжести захвата при его подъёме.
- горизонтальная координата перемещения центра тяжести захвата при его подъёме.
Из первых двух уравнений получены выражения для технологических сил, действующих со стороны захватного устройства на поднимаемые деревья:
P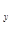
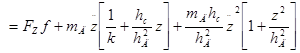 (2)
(2)
P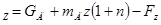 ; P
; P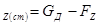 ; P
; P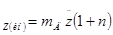 ; где n=
; где n=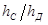 =0,66
=0,66
F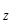 - реакция на крону деревьев со стороны определяется из третьего уравнения системы (1):
- реакция на крону деревьев со стороны определяется из третьего уравнения системы (1):
F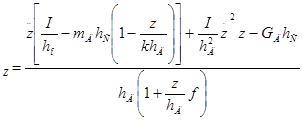 (3)
(3)
Подставив эти выражения в формулы для определения нагрузки, действующей на шток гидроцилиндра навесной системы трактора (рисунок 2) получим дифференциальные уравнения описывающие подъём пачки деревьев:
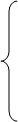
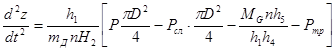 (4)
(4)
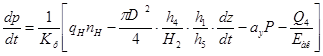 (5)
(5)
где 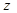 - вертикальная координата захвата, м;
- вертикальная координата захвата, м; 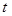 -время, с;
-время, с; 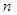 - коэффициент длины дерева;
- коэффициент длины дерева;
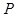 - давление рабочей жидкости гидросистемы, Па;
- давление рабочей жидкости гидросистемы, Па;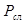 - давление рабочей жидкости в сливной магистрали гидросистемы, Па;
- давление рабочей жидкости в сливной магистрали гидросистемы, Па; 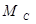 - суммарный момент, сопротивление волочению пачки развиваемый силами тяжести дерева, захвата и навески трактора, Нм;
- суммарный момент, сопротивление волочению пачки развиваемый силами тяжести дерева, захвата и навески трактора, Нм;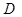 - диаметр гидроцилиндра, м;
- диаметр гидроцилиндра, м; 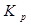 - коэффициент податливости упругих элементов гидропривода, показывающий на сколько увеличивается объём элементов гидросистемы при увеличении давления на единицу, м/Па;
- коэффициент податливости упругих элементов гидропривода, показывающий на сколько увеличивается объём элементов гидросистемы при увеличении давления на единицу, м/Па; 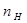 -частота вращения насоса, 1/с;
-частота вращения насоса, 1/с; 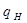 - рабочий объём насоса, м
- рабочий объём насоса, м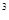 /об; а
/об; а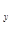 - коэффициент утечек рабочей жидкости, коэффициент утечек, равен отношению расхода рабочей жидкости, утекающей через различные неплотности к давлению в гидросистеме,
- коэффициент утечек рабочей жидкости, коэффициент утечек, равен отношению расхода рабочей жидкости, утекающей через различные неплотности к давлению в гидросистеме, 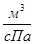 ;
; 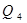 - количество жидкости поступающей в гидроаккумулятор;
- количество жидкости поступающей в гидроаккумулятор; 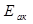 - модуль упругости гидроакумулятора.
- модуль упругости гидроакумулятора.
При решении задачи сделаны следующие допущения: давление в сливной линии не зависит от скорости движения поршня и является величиной постоянной; сила сопротивления трения не зависит от режима работы и является постоянной величиной; частота вращения вала насоса не зависит от нагрузки и является постоянной; все плечи - 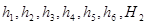 слабо изменяются при перемещении захвата, в первом приближении их также считаем постоянными величинами; площадь сечения штока мала, по сравнению с площадью сечения гидроцилиндра.
слабо изменяются при перемещении захвата, в первом приближении их также считаем постоянными величинами; площадь сечения штока мала, по сравнению с площадью сечения гидроцилиндра.
Суммарный момент М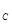 определяется соотношением
определяется соотношением
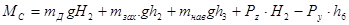 (6)
(6)
где m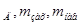 - соответственно, массы дерева, захвата и навесного оборудования,
- соответственно, массы дерева, захвата и навесного оборудования,
g - ускорение свободного падения.
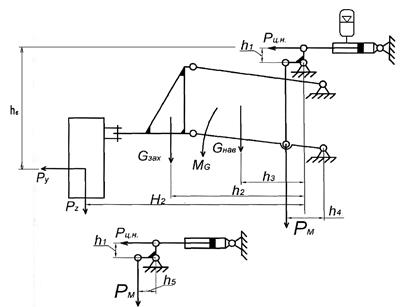
Рисунок 2 - Расчётная схема навесной системы колёсного трактора в агрегате с бесчокерным захватом
Учитывая (4) и (5) условия единственности решения: при t = 0; z = 0;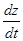 = 0; Р = 0.
= 0; Р = 0. 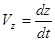 (7), где
(7), где 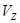 - вертикальная проекция скорости движения захвата;
- вертикальная проекция скорости движения захвата;
Введём следующие обозначения:
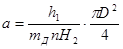 ;
;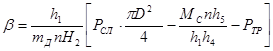 ;
;
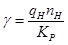 ;
;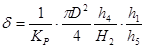 ;
;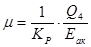
Система исходных уравнений и условия единственности приобретают
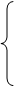
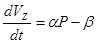
 (8)
(8)
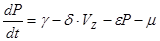 (9)
(9)
P(0) = 0;V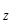 (0)=0.
(0)=0.
Для решения задачи выразим из уравнения (8) давление Р и
подставим его в уравнение (9):
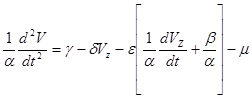 (10)
(10)
Полученное уравнение (10) является обыкновенным линейным неоднородным дифференциальным уравнением второго порядка. Его общее решение определяется как сумма общего решения однородного уравнение и частного решения дифференциального уравнения (10).
Опуская некоторые математические выкладки запишем общее решение дифференциального уравнения
V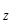 =e
=e (11)
(11)
Дня определения давления Р найдём производную от скорости V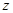 по времени, P(0)=0 с учетом постоянных интегрирования из условий что V
по времени, P(0)=0 с учетом постоянных интегрирования из условий что V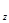 (0)=0; и P(0)=0, найдем выражение для вертикальной координаты Z с учетом постоянной интегрирования из условии Z(0) = 0, опуская некоторые математические выкладки и возвращаясь к исходным переменным -
(0)=0; и P(0)=0, найдем выражение для вертикальной координаты Z с учетом постоянной интегрирования из условии Z(0) = 0, опуская некоторые математические выкладки и возвращаясь к исходным переменным - 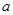 ;
;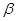 ;
;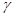 ;
;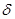 ;
;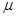 принимая допущения об отсутствии утечек в системе и амплитуды давления и скорости захвата принимают максимальные значения.
принимая допущения об отсутствии утечек в системе и амплитуды давления и скорости захвата принимают максимальные значения.
Получим аналитические выражения для 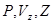 :
:
V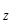 =
=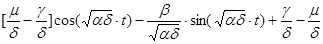 (12)
(12)
P=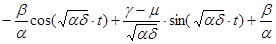 (13)
(13)
Z=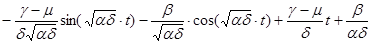 (14)
(14)
Эти выражения (12), (13), (14) могут быть использованы для инженерных расчётов при проектировании гидропривода трелёвочных устройств с рекуперацией энергии.
Библиографический список
1.Смоляницкий, Э.А. Рекуперативный насосно-аккумуляторный гидропривод для мобильных машин-орудий циклического действия [Текст] / Э.А Смоляницкий.- СДМ. 2007. №5.- С. 3-10.
2. Рекуперативный гидропривод почвообрабатывающего агрегата: пат. на изобретение 2294613 Российская Федерация, МПК А01В 63/10, А01В 63/112, А01В 63/111 / В.И. Посметьев, Е.А. Тарасов, В.В. Посметьев, В. С. Кухарев; заяв. и патентообладатель ВГЛТА.-№2005124070/12; заяв.28.07.2005; опубл.10.03.2007, Бул. №7.
3. Жуков А. В. Проектирование лесопромышленного оборудования : [Учеб. для вузов по спец. "Машины и оборуд. лесн. комплекса"] [Текст] / А. В. Жуков, Минск Вышэйш. шк. 1990 - 311с.