The main stages of designing of the turned tasks are presented in this article. Step-by-step procedure of the address of a task is described, methodical recommendations about performance of each step are made, concrete examples of mathematical tasks are given. It is shown that such mathematical activities of school students for independent designing of the vicinity of the turned tasks are a development tool of universal educational actions at mathematics lessons.
Keywords: the address of a mathematical task, the theory and a technique of training in mathematics developing zadachny designs, universal educational actions, modern school students.
В настоящее время происходят глобальные перемены во всей системе образования, так с 1 сентября 2015 г. все общеобразовательные учреждения страны перешли на новый Федеральный государственный образовательный стандарт основного общего образования. Одной из отличительных особенностей данного стандарта является отказ от традиционно сформулированных результатов обучения в виде знаний, умений и навыков и переход к реальным видам деятельности, которыми обучающиеся должны овладеть к концу уже начального обучения. Неотъемлемой частью ядра нового стандарта являются универсальные учебные действия (далее УУД), объединённые в четыре группы: личностные, регулятивные, познавательные и коммуникативные, для которых предусмотрена программа формирования УУД [5].
Непосредственно сам авторский коллектив, разработавший «Программу развития УУД», в широком смысле под этой дефиницией понимает «умение учиться, то есть способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта. В более узком (собственно психологическом значении) этот термин можно определить как совокупность способов действия учащегося (а также связанных с ними навыков учебной работы), обеспечивающих его способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса» [4, с. 27].
Академик РАО А. Г. Асмолов характеризует УУД, как «обобщенные действия, порождающие широкую ориентацию учащихся в различных предметных областях познания и мотивацию к обучению» [4].
Необходимо отметить и то, что разработчики стандарта определили не только предметные, но и личностные и метапредметные образовательные результаты. Не акцентируя внимание на существенные недостатки данного стандарта, отметим, что в нем среди метапредметных результатов выделены следующие УУД:
- умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
- умение оценивать правильность выполнения учебной задачи, собственные возможности её решения;
- умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач [1].
Вызывает сомнение, что традиционное содержание обучения математике позволит в полной мере развить вышеперечисленные УУД. Однако нам видится, что одним из возможных путей решения указанной проблемы является развитие навыка самостоятельного составления школьниками обращённых математических задач.
Не останавливаясь на дидактическом и развивающем потенциале обращенных задач, уже раскрытых автором в статье [2], перейдём к рассмотрению процесса обращения задачи с позиции построения некоторого алгоритма, в котором расписана последовательность действий, применяемых для конструирования обращённых задач.
Итак, пусть решена следующая задача:
Задача 1. Лыжник поднимался в гору 3 минуты со скоростью 150 метров в минуту, а с горы спускался 2 минуты со скоростью 300 метров в минуту. Найти среднюю скорость лыжника в минуту.
Решение:
1) 150 ·3 = 450 (м),
2) 300 ·2 = 600 (м),
3) 3+2 = 5 (мин),
4) 450+600 =1050 (м),
5) 1050:5 = 210 (м/мин) — средняя скорость лыжника.
Придерживаясь рекомендаций, сформулированных академиком П. М. Эрдниевым по записи поэлементного состава условия и требования решенной исходной задачи в виде числовой цепочки, присоединяя к ней и найденное искомое, заключено в рамочку, позволит школьникам целостно представить весь поэлементный состав задачи [6].
Так, после решения этой задачи учитель проводит следующую беседу (в скобках даны примерные ответы учащихся):
— Сколько чисел было дано в условии решенной задачи? Какие это числа? Выпишите их. (В задаче были даны четыре числа: 3 мин, 150 м/мин, 2 мин, 300 м/мин).
— В условии задачи были даны четыре числа, пятое найдено при решении — это ответ задачи — 210 м/мин. Запишем ответ в рамочке, таким образом, мы с вами составили числовую цепочку структурных элементов решённой задачи (Рис.1):
![]()
Рис.1. Числовая цепочка структурных элементов задачи 1
После этого составляются всевозможные числовые цепочки обращённых задач, в которых искомым элементом последовательно выступает каждый элемент данной задачи или их комбинация.
Заметим, что обращённых задач можно построить несколько в зависимости от числа данных и искомых. Причём эта зависимость между числом данных и искомых и числом обратных задач имеет вид:
P = (2n-1)(2k-1),
где Р — потенциал обращения задачи, n — число данных задачи, k — число искомых задачи.
Таким образом, учитель может заранее просчитывать возможное количество получения обращённых задач из данной задачи.
Далее учитель поясняет процесс составления обращённых задач:
— Если поменять местами число 210 м/мин с любым из четырех других чисел, то мы получим новую задачу. Например, вместо числа 210 м/мин сделаем искомым число 3 мин, и заключим его в рамочку, а число 210 м/мин пусть будет известным, его мы введём в условие обращённой задачи. Числовая цепочка структурных элементов этой обращённой задачи будет иметь вид 1.1 (Рис.2.):
![]()
Рис.2. Числовая цепочка структурных элементов (вид 1.1)
Следующий шаг работы над обращением задачи заключается в осуществлении школьниками целенаправленного перебора возможных вариантов выбора искомого и данных обращённых задач. Составлять всевозможные числовые цепочки обращённых задач учащиеся могут самостоятельно. В ходе этой работы учитель может поставить перед учащимися вопросы: «Кто быстрее составит всевозможные числовые цепочки новых задач?», «Кто больше составил числовых цепочек?» и т. д. Организованная таким образом самостоятельная работа по составлению числовых цепочек обращённых задач даёт возможность каждому школьнику занять активную творческую позицию.
В результате последовательной реализации обращения исходной задачи числовые цепочки структурных элементов всех обращённых задач будут следующими (Рис.3):
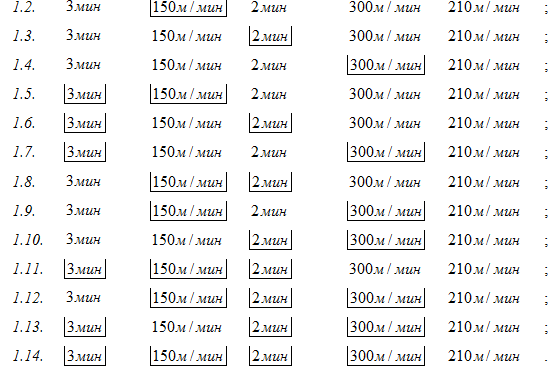
Рис. 3. Числовые цепочки структурных элементов всех обращенных задач
При составлении числовых цепочек обращённых задач учащиеся нередко пытаются включить в условие результаты промежуточных действий (так, в нашем примере они могут попытаться использовать числа 450, 600 и др.). Учитель должен указать, что в условие обращённых задач включается лишь ответ задачи.
Поскольку такую работу они не выполняли ранее, для проверки результатов этой части задания можно использовать взаимоконтроль. Отметим, что организация взаимопроверки в парах важна также с точки зрения формирования действий самоконтроля и самооценки. В процессе такой проверки ученик учится соотносить выполненные одноклассником действия с заранее определёнными критериями и вместе с тем, анализируя действия товарища, он непроизвольно оценивает свои действия.
Затем, по полученным числовым цепочкам структурных элементов задачи школьники формулируют условие и требование обращённых задач. Учащийся, видя число без рамочки, включает его в условие задачи, а число в рамочке в её требование, поскольку оно должно быть скрыто, т. е. сделано неизвестным, и для него он подбирает соответствующий вопрос. Таким образом, числа, заключенные в рамочку, становятся своеобразными опорными пунктами для составления формулировок обращённых задач.
— Каков будет вопрос обращённой задачи 1.2? («С какой скоростью поднимался лыжник в гору?»).
— Составьте текст новой задачи 1.2. Для этого в условии расскажите про четыре оставшихся числа.
Школьники составляют такую обращённую задачу:
Задача 1.2. Лыжник поднимался в гору 3 минуты с некоторой скоростью, а с горы спускался 2 минуты со скоростью 300 метров в минуту. Средняя скорость лыжника в минуту — 210 метров. С какой скоростью поднимался лыжник в гору?
Решение этой обращённой задачи для школьников трудности не составляет. А вот само по себе составление такой задачи и её решение, приводящее к изменению известного хода умозаключений, что имеет несомненное значение для развития гибкости мышления учащихся.
После решения обращённой задачи полезно иногда сравнивать условия обеих задач, а также способы их решения.
— Чем отличаются друг от друга прямая и обращённая задача? Какие числа являются искомыми в прямой и обращённой задачах?
— Сравним решения прямой и обращённой задач. Что здесь общего?
— Какими действиями решается каждая задача?
— Рассмотрите действия задачи 1 и 1.2. Какие действия одинаковы?
Подобные беседы проводятся обычно не полностью, а частично, для выявления отдельных зависимостей между прямой и обращённой задачами.
Конечно, можно ограничиться составлением и решением одной обращённой задачи 1.2, но для развития гибкости мышления школьников, а также их творческих способностей, после конструирования и решения первой обращённой задачи 1.2 перед учащимися целесообразно поставить задачу нахождения и других обращённых задач.
Можно составить также обращённую задачу и по числовой цепочке 1.3, где в качестве искомого выбрано время спуска лыжника с горы и оставлена известной средняя скорость лыжника.
Задача 1.3. Лыжник поднимался в гору 3 минуты со скоростью 150 м, а с горы спускался несколько минут, проезжая в каждую минуту по 300 м. Средняя скорость лыжника на всем пути была равна 210 м. Определить время спуска лыжника.
А можно организовать работу по обращению задачи следующим образом. Предложить учащимся восстановить текст задачи, пользуясь числовой цепочкой, к примеру, 1.4.
«Заполните пропуски в тексте задачи, составленной на основе данных исходной задачи. Сформулируйте вопрос и решите получившуюся задачу».
Задача 1.4. Лыжник поднимался в гору … со скоростью 150 метров в минуту, а с горы спускался … с некоторой скоростью. Средняя скорость лыжника в минуту составляет 210 м. Вопрос?
Можно предложить и такое задание.
«Из составленных числовых цепочек структурных элементов данной задачи выберите ту (те), в которой требуется найти время и скорость подъёма лыжника в гору. Решите её».
Собственно говоря, составление и решение обращённых задач — в психологическом плане очень ценная работа, развивающая гибкость мышления учащихся:
- Преобразуя задачу, дети выявляют и используют взаимно обратные связи между величинами: если в прямой задаче, скажем, определялось расстояние по скорости и времени, то в обращённой — определяется, к примеру, время по расстоянию и скорости.
- Школьники практически познают связи между действиями: если в прямой задаче использовалось умножение, то при решении обращённой применено действие, обратное умножению, т. е. деление.
- Решая обращённые задачи, школьники, перестраивают суждения и умозаключения, использованные при решении прямой задачи, преодолевая при этом в мышлении инерцию действий, выполненных при решении прямой задачи [1].
Таким образом, составление на уроках математики обращенных задач позволит разнообразить урок, привлечь внимание школьников к изучаемому материалу, приобщить их к математической деятельности, что повысит уровень их активности и в итоге окажет положительное влияние на развитие интеллектуальных способностей и личностных качеств учащихся [3]. И наконец, умение оценивать собственные возможности в выполнение учебной задачи является одним из важных познавательных УУД.
Литература:
- Зайкин, М.И., Абрамова, О. М. О функциональных и структурных отличиях понятий обратной и обращенной задачи // Мир науки, культуры, образования. — 2012. — № 6(37). — С. 152–154.
- Абрамова, О. М. Обращение школьной задачи как основа современных технологий обучения в математическом образовании // Педагогика и просвещение. — 2014. — № 3. — С. 30–41.
- Артюхина, М. С. Интеллектуальное воспитание обучающихся в контексте интерактивных технологий обучения // Педагогика и просвещение. — 2014. — № 4. — С. 42–50.
- Как проектировать универсальные учебные действия в начальной школе. От действия к мысли: пособие для учителя / А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская и др. — М.: Просвещение, 2010. — 152 с.
- Приказ Министерства образования и науки РФ от 17 декабря 2010 г. № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования».
- Эрдниев, П. М. Методика упражнений по математике — М.: Просвещение, 1970. — 319 с.

