В начале статьи рассмотрен классический пример продольного изгиба упругого стержня, шарнирно опертого по концам. Выводится дифференциальное уравнение изогнутой оси стержня и находится критическая сила — сила Эйлера. В продолжение идеи ставится задача о нахождении силы Эйлера в случае стержня с начальной неправильностью. Анализируется зависимость стрелы прогиба от внешней силы и определяется критическая нагрузка.
Ключевые слова: продольный изгиб, критическая сила, сила Эйлера, стержень с начальной неправильностью.
Потеря устойчивости — одна из наиболее распространенных проблем стержней, работающих на сжатие. Стержни, в основном, используются в различных строительных конструкциях; именно они образуют так называемую «фундаментальную основу» зданий и сооружений.
Элемент конструкции может иметь три равновесных состояния: устойчивое, неустойчивое и безразличное. Равновесие называют устойчивым, если при достаточно малом воздействии на систему, она, совершив затухающие колебания около положения равновесия, возвращается в первоначальное состояние. Иначе, если система под действием внешнего возмущения продолжает свое движение (в нашем случае, если стержень продолжает деформироваться), то говорят, что равновесие является неустойчивым.
Нас интересует переходное — критическое состояние, при котором система находится в безразличном равновесии. При малом отклонении она не возвращается в первоначальное положение, при этом ее движение прекращается. Нагрузка, при которой система из устойчивого равновесия переходит в неустойчивое, называется критической.
Для того чтобы понять, что такое критическая сила, рассмотрим случай потери устойчивости упругого стержня. Такой случай еще называется продольным изгибом.
Эйлерова сила. Рассмотрим прямолинейный стержень длины l, постоянного поперечного сечения I, который сжимается под действием внешней силы P. Пусть один конец имеет неподвижное закрепление, другой — подвижное (например, подвижный шарнир).
Заметим, что в реальной жизни ось стержня меняет свою длину под действием внешней силы P. Мы этого учитывать не будем; считаем, что прогибы малы (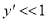 ) по сравнению с длиной стержня, и подвижный конец не смещается. Тогда выражение для кривизны
) по сравнению с длиной стержня, и подвижный конец не смещается. Тогда выражение для кривизны 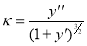 преобразуется к виду:
преобразуется к виду: 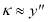 .
.
Используем выражение для кривизны изогнутой оси стержня [1]:
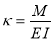 ,(1)
,(1)
где M — изгибающий момент, E — модуль Юнга, I — момент инерции поперечного сечения.
Определим изгибающий момент в некотором сечении. Рассмотрим часть стержня, находящегося в равновесии (рис. 1). Сумма моментов относительно точки O равна нулю.
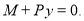 (2)
(2)
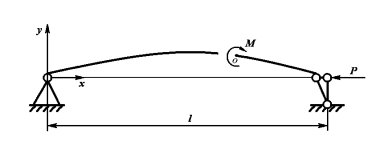
Рис. 1.
Из (1) и (2) следует
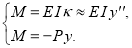
Таким образом, получили дифференциальное уравнение изогнутой оси стержня
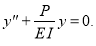 (3)
(3)
Общее решение уравнения (3) имеет вид
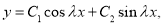 где
где 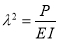 .
.
Для определения неизвестных констант 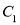 и
и 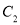 используем два начальных условия
используем два начальных условия
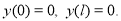
Из первого следует, что 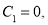 а из второго получим
а из второго получим
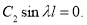
Константа 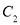 не равна нулю (иначе получим тривиальное решение
не равна нулю (иначе получим тривиальное решение 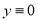 , что соответствует прямолинейной форме равновесия). Следовательно,
, что соответствует прямолинейной форме равновесия). Следовательно, 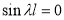 , т. е.
, т. е.
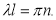
Таким образом, получили
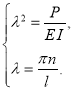 (4)
(4)
Из системы (4) находим P
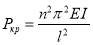 ,
,
где n — произвольное целое число; т. е. получили последовательный ряд значений силы P.
Наименьшая сила P, отличная от нуля, будет при 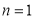 :
:
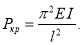 (5)
(5)
Эту формулу впервые получил Л. Эйлер [2]. Cилу 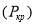 , при которой прямолинейная форма равновесия перестает быть устойчивой, называют эйлеровой силой (далее —
, при которой прямолинейная форма равновесия перестает быть устойчивой, называют эйлеровой силой (далее — 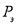 ).
).
При 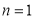 уравнение изогнутой оси стержня принимает вид
уравнение изогнутой оси стержня принимает вид
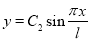 .
.
Последнее уравнение задает первую из отклоненных форм равновесия стержня [3].
Стержень с начальной неправильностью. Пусть стержень изначально имеет не прямолинейную, а искривленную форму. В точках 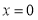 и
и 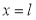 шарнирное опирание.
шарнирное опирание.
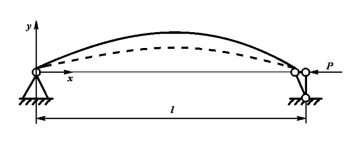
Рис. 2.
Уравнение равновесия с учетом начального прогиба
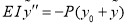 ,(6)
,(6)
где 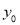 — начальная форма стержня (на рис. 2 — пунктирная линия),
— начальная форма стержня (на рис. 2 — пунктирная линия),
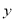 — дополнительное отклонение, приобретаемое упругим стержнем под действием внешней силы
— дополнительное отклонение, приобретаемое упругим стержнем под действием внешней силы 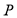 .
.
Пусть, например, начальная форма стержня имеет такой вид
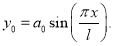 (7)
(7)
Преобразуем уравнение (6) с учетом выражения (7)
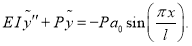
Разделим последнее уравнение на 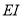 и сделаем замену
и сделаем замену 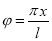 :
:
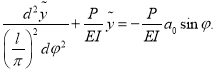 (8)
(8)
Примечание. Замена 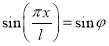 корректна, т. к.
корректна, т. к. 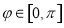 .
.
Домножим уравнение (8) на 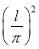 и используем значение силы Эйлера (5) для шарнирного закрепления на концах стержня. Тогда с учетом замены
и используем значение силы Эйлера (5) для шарнирного закрепления на концах стержня. Тогда с учетом замены 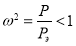 , получим:
, получим:
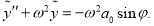 (9)
(9)
Общее решение неоднородного дифференциального уравнения (9) имеет вид
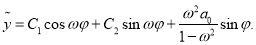
Для определения неизвестных констант 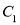 и
и 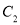 используем два начальных условия
используем два начальных условия
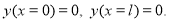
Учитывая замену 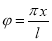 , получаем:
, получаем:
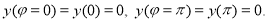
Из первого условия следует, что 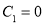 , а из второго —
, а из второго — 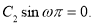
Так как 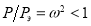 , то
, то 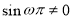 , следовательно,
, следовательно, 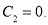
С учетом известных констант запишем общее решение
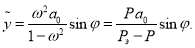
Сделаем обратную замену
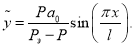
Таким образом, первая из отклоненных форм равновесия стрежня с учетом начального прогиба имеет вид
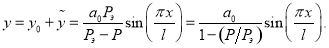
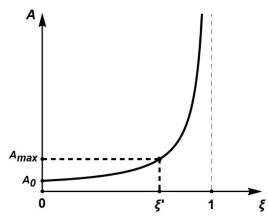
Рис. 3.
На рис. 3 представлен график зависимости стрелы прогиба от безразмерной величины 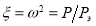 , характеризующей связь между значениями внешней силы
, характеризующей связь между значениями внешней силы 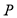 и силой Эйлера
и силой Эйлера 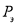 . При
. При 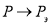 , получаем
, получаем 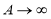 , т. е. стрела прогиба неограниченно возрастает. Отметим, что максимальное значение стрелы прогиба определяется проектировщиком с использованием строительных норм и правил (СНиП). Поэтому в данном случае критическая сила будет равна не силе Эйлера, т. е. при
, т. е. стрела прогиба неограниченно возрастает. Отметим, что максимальное значение стрелы прогиба определяется проектировщиком с использованием строительных норм и правил (СНиП). Поэтому в данном случае критическая сила будет равна не силе Эйлера, т. е. при 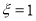 , а какой-то другой силе
, а какой-то другой силе 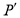 , причем
, причем 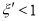 . Таким образом ставится задача нахождения
. Таким образом ставится задача нахождения 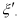
Пусть задано максимальное значение стрелы прогиба — Amax. Тогда имеем
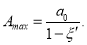
Отсюда безразмерная величина 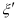 равна
равна
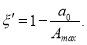 (10)
(10)
Используя выражение 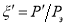 и уравнение (10), получим
и уравнение (10), получим 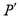
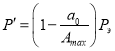 .
.
Следовательно, стержень можно нагрузить силой 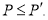
Литература:
1. Феодосьев В. И. Сопротивление материалов: учебник для вузов. М.: Изд-во МГТУ им. Н. Э. Баумана, 1999. 592 с.
2. Вольмир А. С. Устойчивость деформируемых систем. М.: Изд-во «Наука», 1967. 984 с.
3. Ванько В. И. Очерки об устойчивости элементов конструкций. М.: Изд-во МГТУ им. Н. Э. Баумана, 2014. 223 с.

