Наиболее быстрым способом строительства ледовых речных переправ традиционно является замораживание мелко дробленого льда в ледяной воде. Экспериментально нами установлено, что более прочен ледовый настил из круглозернистого гранулята, получаемого в кипящем слое [1].
В работах [1,2] показано, что охлажденная сферическая гранула льда адиабатически намораживает на своей поверхности слой льда, движение наружной границы которого соответствует условиям одномерной однофазной задачи Стефана [3-5] с заданием постоянной температуры на границе фазового перехода, предложена математическая модель и алгоритм численного решения краевой задачи с подвижной границей фазы, найдена зависимость кинетики роста толщины намораживаемого слоя от времени и функция зависимости максимально возможного радиуса гранулы льда от его начальной температуры, и закон изменения температуры внутри гранулы в процессе намораживания льда.
В данной статье на основе математического моделирования рассматривается элементарный акт адиабатического смерзания двух ледяных шаров с целью определения его кинетических характеристик и последующего построения обобщенной модели для всего слоя из круглозернистого гранулята.
Процесс смерзаемости двух гранул в ледяной воде сопровождается как теплообменом – передачей тепла от воды льду, так и внешними признаками – «обрастанием» ледяных гранул оболочкой изо льда с образованием фигуры с быстро растущей перемычкой между гранулами. Граница лед-вода фигуры подвижная. Во времени динамично меняются не только ее размеры, расстояния точек границы фигуры от центров гранул и продольной ее оси симметрии, но и форма, угол и радиус закругления щели между шарами.
В однофазном варианте математическая модель смерзания двух шаров льда (рис. 1 и 2) представляет собой следующую начально-краевую задачу:
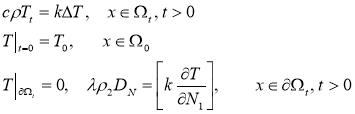 (1)
(1)
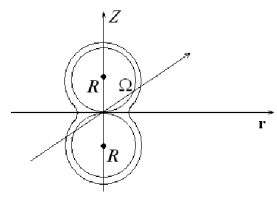
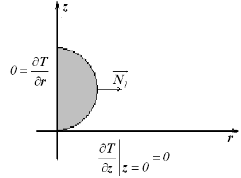
Рис. 1Рис. 2
В задаче (1) температура Т определяется из уравнения теплопроводности ![]() , где с – коэффициент теплоемкости, k – коэффициент теплопроводности,
, где с – коэффициент теплоемкости, k – коэффициент теплопроводности, ![]() - плотность вещества.
- плотность вещества.
![]() граничные условия,
граничные условия, ![]() начальное условие. Фазовый переход сопровождается выделением (или поглощением) определенного количества тепла. Поэтому тепловой поток на границе фазового перехода разрывен и определяется величиной
начальное условие. Фазовый переход сопровождается выделением (или поглощением) определенного количества тепла. Поэтому тепловой поток на границе фазового перехода разрывен и определяется величиной 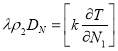 . Здесь
. Здесь ![]() - энтальпия фазового перехода, а
- энтальпия фазового перехода, а ![]() - скорость движения границы фазового перехода по нормали. Из симметричности данных будем рассматривать задачу для правой части верхней гранулы. Рассматриваемая задача Стефана (1) может быть записана в виде одного общего уравнения теплопроводности во всей области
- скорость движения границы фазового перехода по нормали. Из симметричности данных будем рассматривать задачу для правой части верхней гранулы. Рассматриваемая задача Стефана (1) может быть записана в виде одного общего уравнения теплопроводности во всей области ![]() [5]:
[5]:
![]() (2)
(2)
В уравнении (2) ![]() - дельта – функция.
- дельта – функция.
Коэффициенты теплоемкости и теплопроводности разрывны и имеют вид:
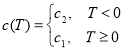
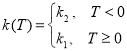 (3)
(3)
Простейший подход к приближенному решению задачи Стефана в формулировке (2) – (3) состоит в том, что коэффициенты уравнения (2) сглаживаются, то есть совершается переход к обычной задаче теплопроводности.
В уравнении (2) теплоемкость с(Т) и слагаемое ![]() входят одинаковым образом. Заменим
входят одинаковым образом. Заменим ![]() - функцию
- функцию ![]() некоторой функцией
некоторой функцией ![]() , которая отлична от нуля только внутри интервала сглаживания
, которая отлична от нуля только внутри интервала сглаживания ![]() , и введем эффективную сглаженную теплоемкость
, и введем эффективную сглаженную теплоемкость
![]() ,
,
При условии сохранения баланса тепла на [-Δ, Δ] используем параболическую аппроксимацию
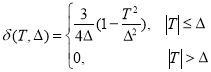 , где
, где 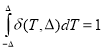 .
.
Проведем также сглаживание коэффициента теплопроводности k(T):
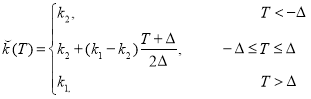
Здесь ![]() коэффициенты теплопроводности для льда и воды соответственно.
коэффициенты теплопроводности для льда и воды соответственно.
Осуществим переход к безразмерным переменным, начиная с выбора характерных значений в модели. В качестве масштаба измерения пространственной переменной ![]() можно взять длину радиуса L — линейный масштаб. Используя для безразмерных переменных те же обозначения, что и для размерных, но со штрихом, имеем
можно взять длину радиуса L — линейный масштаб. Используя для безразмерных переменных те же обозначения, что и для размерных, но со штрихом, имеем ![]() , где
, где ![]() — безразмерная переменная. В качестве масштаба температуры можно взять абсолютное значение начальной температуры:
— безразмерная переменная. В качестве масштаба температуры можно взять абсолютное значение начальной температуры: ![]() , где
, где ![]() — безразмерная температура. Аналогично пусть
— безразмерная температура. Аналогично пусть ![]() , где характерный масштаб времени t0 пока не определен. В результате получили следующую замену:
, где характерный масштаб времени t0 пока не определен. В результате получили следующую замену:
![]() ;
; ![]() ;
; ![]()
Подстановка в уравнение (2) приводит к уравнению в безразмерных переменных:
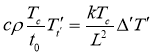 или
или 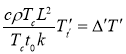
Если 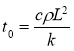 , то
, то 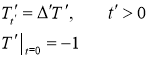
Параметр L выберем так, чтобы начальный шар имел единичный радиус (L=R).
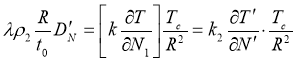
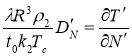 ;
; 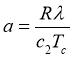 ;
; 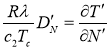
В итоге, получим:
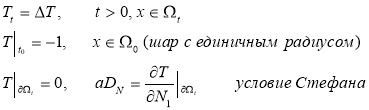
Запишем задачу в цилиндрической системе координат:
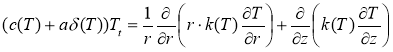
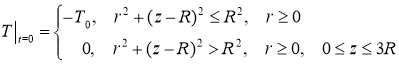
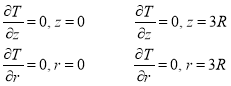
Будем решать задачу с осевой симметрией, то есть решение не будет зависеть от угла φ (в цилиндрической системе координат (![]() ). Через 3R обозначены границы воды.
). Через 3R обозначены границы воды.
Так как L=R, то в твердой фазе:
![]() ;
; 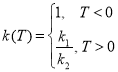
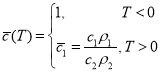 ;
; ![]() ;
; ![]()
Где ![]() - коэффициент теплоемкости в новых переменных.
- коэффициент теплоемкости в новых переменных.
Следовательно, в новых переменных:
![]() (4)
(4)
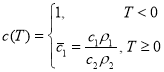
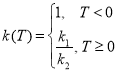 (5)
(5)
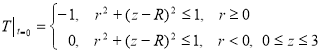
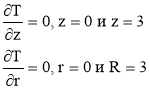 (6)
(6)
Для численного решения задачи (4)-(6) использовались локально-одномерные неявные разностные схемы. При этом итоговые системы линейных алгебраических уравнений решались методом прогонки. Результаты численных оценок размеров перемычек согласуются с результатами эксперимента, графики эмпирических зависимостей роста размеров перемычек Sn от размеров диаметров шаров dn приведены на рис. 3. Здесь n=0, 1, ..., 12 – число погружений на 60 сек., каждое с перерывами для сушки на 1 час. Аналитической аппроксимацией этих графиков могут служить соотношения:
dn = 25 + ![]() , Sn = 8,286 · n0.577, n
, Sn = 8,286 · n0.577, n![]() [0;12](7)
[0;12](7)
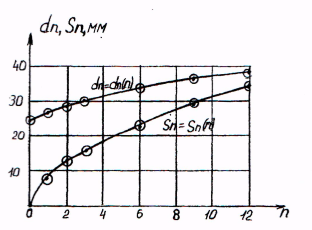
Рис. 3. Графики зависимости роста диаметров dn шаров и перемычки Sn от числа погружений n (по 60 сек.).
Список использованных источников
- Математическая модель намораживания гранул льда для ледовых переправ в виде задачи Стефана / А.С. Ащеулова, A.А. Храпов, В.В. Рагулин, В.И. Полтавцев // Бурение и нефть. - 2007 -№4 - с.17-19.
- Задача Стефана для адиабатического намораживания воды холодом гранул / А.С. Ащеулова, А.А. Храпов, B.В. Рагулин, В.И. Полтавцев // Вестник КрасГАУ. -2007. -№1.-с.26-30
- Рубинштейн Л.И. Проблема Стефана. – Рига: Звайгзне, 1967. – 457с.
- Мейрманов A.M. Задача Стефана. - Новосибирск: Наука, 1986
- Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. -М.: Едиториал УРСС, 2003

