Теоретико-игровая модель конкурентной борьбы за рынки сбыта продукции
Автор: Власов Дмитрий Анатольевич
Рубрика: Экономическое развитие и рост
Опубликовано в Вопросы экономики и управления №5 (7) ноябрь 2016 г.
Дата публикации: 22.09.2016
Статья просмотрена: 591 раз
Библиографическое описание:
Власов, Д. А. Теоретико-игровая модель конкурентной борьбы за рынки сбыта продукции / Д. А. Власов. — Текст : непосредственный // Вопросы экономики и управления. — 2016. — № 5 (7). — С. 27-29. — URL: https://moluch.ru/th/5/archive/44/1267/ (дата обращения: 27.04.2024).
Теоретико-игровая модель конкурентной борьбы за рынки сбыта продукции
Власов Дмитрий Анатольевич, кандидат педагогических наук, доцент
Российский экономический университет имени Г. В. Плеханова (г. Москва)
В центре внимания статьи — построение и направления исследования теоретико-игровой модели конкурентной борьбы за рынки сбыта продукции. Поставлены актуальные вопросы формализации экономической ситуации, предложены варианты оптимизационных подходов игроков, выполнен анализ категории «конкуренция» с современной точки зрения.
Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие
Современными характеристиками потребительского спроса являются продукция и технико-экономический потенциал производителя. Конкуренция в рыночной экономике играет особую роль, связанную с интеграцией потребительских запросов и возможностей производителей по обеспечению производства продукции. Она ставит важную задачу повышения конкурентоспособности продукции. Естественно, что как конкурентные недостатки, так и конкурентные преимущества возникают в процессе производства и потребления продукции. Традиционно конкуренцию мы воспринимаем как борьбу за достижение оптимальных результатов (по одному или нескольким критериям оптимальности, например, «Доход», «Риск», «Цена», «Цена — Качество», «Цена — Качество — Послепродажная поддержка» и др.) [4]. Мы убеждены, что в современных условиях, характеризующихся переходом к инновационной экономике, конкуренция должна остаться формой здорового соперничества экономических субъектов.
В условиях отрицательной динамики объема платежеспособного спроса потребителей (с 2014 года) и наличия на рынке достаточного числа независимых продавцов, характерного для настоящей экономической ситуации, конкурентная борьба за рынки сбыта продукции принимает все более острую форму. Зачастую предприниматели, стремясь получить единовременную прибавку к доходу принимают из всех возможных стратегий развития выбирают крайние стратегии (в глобальном смысле не являющиеся оптимальными), стремясь «выжить», удержаться «на плаву» не думают стратегическом развитии, долгосрочном сохранении рынка сбыта продукции, часто подвергают критике феномен «конкуренция» и игнорируют достижения теории принятия решений [6]. Нередки случаи, когда стремление нескольких фирм улучшить собственное положение на рынке реализации товаров, наоборот приводят к ухудшению положения этих фирм, падению их общего дохода (нарушение равновесия Дж.Нэша). Однако конкурентная борьба — это единственный способ выживания и развития, создающий условия для совершенствования производства товаров, внедрения наукоемких технологий, способствующий снижению цены на конечный продукт производства.
Существенное значение в конкурентной борьбе приобретает множество стратегий поведения субъектов конкурентного соперничества [7], (стратегия сохранения, стратегия вытеснения конкурента с рынка сбыта продукции, стратегия расширения рынка за счет привлечения новых покупателей и др.). Усиление позиции на рынке в большинстве случаев связаны с ослаблением позиций соперников. Полное вытеснение с рынка приводит к существенным убыткам, частичное вытеснение с рынка характеризуется умеренной динамикой снижения дохода.
Сложность и многоаспектность конкурентной борьбы за рынки сбыта продукции требует применения самого современного, специального математического аппарата — теории игр [3]. При этом теоретико-игровая модель («Множество игроков», «Множество стратегий игроков», «Функция выигрышей») выступает вариантом формализации конкурентной борьбы. В контексте построения теоретико-игровой модели конкурентной борьбы за рынок сбыта продукции интересен подход, предложенный американским экономистом Майклом Юджином Портерем. Сводя конкуренцию к системообразующей категории «Конкурентный климат», М Портер [8], отмечал необходимость многоаспектного понимания ее структуры. Мы предлагаем следующий вариант количественной интерпретации ее компонентов: вероятность появления новых фирм — конкурентов; вероятность появления товаров-заменителей (к перечню уже имеющихся); склонность поставщиков ресурсов к повышению цен; склонность потенциального покупателя к повышению цен; оптимизационный подход к соперничеству конкурирующих фирм между собой.
Далее в рамках данной статьи построим относительно простую теоретико-игровую модель и представим рекомендации по её дальнейшему исследованию. Предположим, что фирма ![]() занимается производством сезонного товара, имеющего спрос в течение
занимается производством сезонного товара, имеющего спрос в течение ![]() единиц времени. Она имеет возможность поставить товар на рынок в один из моментов времени
единиц времени. Она имеет возможность поставить товар на рынок в один из моментов времени ![]() . Фирма
. Фирма ![]() производит товар с аналогичными характеристиками. Она обладает таким же множеством стратегий вывода товара на рынок: товар, производимый фирмой
производит товар с аналогичными характеристиками. Она обладает таким же множеством стратегий вывода товара на рынок: товар, производимый фирмой ![]() поступает на рынок в один из моментов времени
поступает на рынок в один из моментов времени ![]() . Цель фирмы
. Цель фирмы ![]() — разорение фирмы
— разорение фирмы ![]() , захват освободившегося рынка сбыта продукции. Ограничим законные средства конкурентной борьбы двух фирм выбором момента поставки товара на рынок (понижение цены не предусмотрено). Очевидно, что с целью разорения фирмы
, захват освободившегося рынка сбыта продукции. Ограничим законные средства конкурентной борьбы двух фирм выбором момента поставки товара на рынок (понижение цены не предусмотрено). Очевидно, что с целью разорения фирмы ![]() фирма
фирма ![]() следует минимизировать доход конкурента. Опишем далее технологию выпуска товара. Предположим, что чем дольше товар находится в производственном процессе, и, следовательно, позже поступает к потребителю, тем выше его качество (использование новых технологий, более современное оборудование, иные технические условия производства — больший срок «выдержки» и др.). Считаем, что при наличии товара по одной и той же цене, реализуется только товар более высокого качества (позже поставленный на рынок).
следует минимизировать доход конкурента. Опишем далее технологию выпуска товара. Предположим, что чем дольше товар находится в производственном процессе, и, следовательно, позже поступает к потребителю, тем выше его качество (использование новых технологий, более современное оборудование, иные технические условия производства — больший срок «выдержки» и др.). Считаем, что при наличии товара по одной и той же цене, реализуется только товар более высокого качества (позже поставленный на рынок).
Пусть
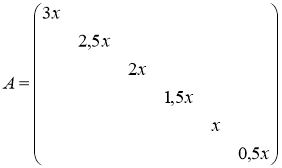 (1)
(1)
Принципиально иную ситуацию можно наблюдать, если фирма ![]() поставит товар на рынок раньше, чем это сделает конкурирующая фирма
поставит товар на рынок раньше, чем это сделает конкурирующая фирма ![]() . Например, фирма
. Например, фирма ![]() выбирает поставку товара в момент времени
выбирает поставку товара в момент времени ![]() , а фирма
, а фирма ![]() в момент времени
в момент времени ![]() . В этом случае товар, произведенный первой фирмой продержится на рынке только первый период, так как со второго периода в наличии товар более высокого качества, произведённый фирмы
. В этом случае товар, произведенный первой фирмой продержится на рынке только первый период, так как со второго периода в наличии товар более высокого качества, произведённый фирмы ![]() . Доход фирмы
. Доход фирмы ![]() будет равен
будет равен ![]() д.е. Если фирма
д.е. Если фирма ![]() не будет спешить с моментов поставки товара на рынок, а выберет стратегию повышения качества товара, то выигрыши фирмы
не будет спешить с моментов поставки товара на рынок, а выберет стратегию повышения качества товара, то выигрыши фирмы ![]() будут равны
будут равны ![]() д.е. Аналогичные рассуждения позволяют определить остальные элементы матрицы, располагающиеся выше главной диагонали.
д.е. Аналогичные рассуждения позволяют определить остальные элементы матрицы, располагающиеся выше главной диагонали.
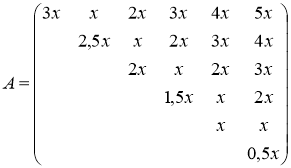 (2)
(2)
Рассмотрим третий принципиальный случай. Его сущность заключается в том, что фирма ![]() не стремится как можно быстрее поставить товар на рынок, а выбирает своеобразную выжидательную стратегию, акцентируя внимание на повышение качества товара. Например, фирма
не стремится как можно быстрее поставить товар на рынок, а выбирает своеобразную выжидательную стратегию, акцентируя внимание на повышение качества товара. Например, фирма ![]() выбирает поставку товара в момент времени
выбирает поставку товара в момент времени ![]() , а фирма
, а фирма ![]() в момент времени
в момент времени ![]() . В этом случае товар второй фирмы продержится на рынке только один период, до выхода на рынок товара фирмы — конкурента. Товар фирмы
. В этом случае товар второй фирмы продержится на рынке только один период, до выхода на рынок товара фирмы — конкурента. Товар фирмы ![]() будет пользоваться спросом оставшиеся пять периодов продаж, т. е. её суммарный доход составит
будет пользоваться спросом оставшиеся пять периодов продаж, т. е. её суммарный доход составит ![]() . Следуя только что описанной логике, вычислим оставшиеся элементы матрицы.
. Следуя только что описанной логике, вычислим оставшиеся элементы матрицы.
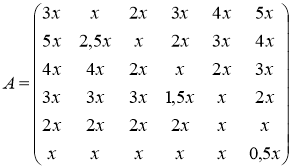 (3)
(3)
В функциональной форме (игра в таком случае считается нормально заданной) матрица выигрышей фирмы ![]() имеет вид:
имеет вид:
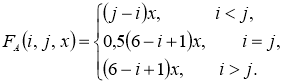 (4)
(4)
После реализации важного этапа математического моделирования экономической ситуации — формализации, необходимо последующее исследование, которое видится в следующем: уточнение типа игры с учетом классификации игр (например, является ли построенная игра игрой с нулевой суммой [6]); применение принципа доминирования (мажорирования) стратегий, позволяющего уменьшить размерность платежной матрицы посредством исключения заранее невыгодных стратегий; исследование на предмет наличия равновесия (единственное или множественное равновесие, отсутствие равновесия) [6]; применение аппарата чистых стратегий (при наличии равновесия), заключающегося в выделении чистой максиминной стратегии фирмы ![]() и чистой минимаксной стратегии фирмы
и чистой минимаксной стратегии фирмы ![]() , позволяющих получить наилучший гарантированный результат в наихудших условиях (оптимизационный принцип, Дж. Нэш); применение аппарата смешанных стратегий (при отсутствии равновесия), подразумевающего поиск решения в виде смешанной стратегии. Последующая реализация информационных технологий [1] позволит оценить применение стратегий выхода товара фирмы
, позволяющих получить наилучший гарантированный результат в наихудших условиях (оптимизационный принцип, Дж. Нэш); применение аппарата смешанных стратегий (при отсутствии равновесия), подразумевающего поиск решения в виде смешанной стратегии. Последующая реализация информационных технологий [1] позволит оценить применение стратегий выхода товара фирмы ![]() на рынок с вероятностных позиций (наиболее вероятна, наименее вероятна, равновероятные стратегии и др.).
на рынок с вероятностных позиций (наиболее вероятна, наименее вероятна, равновероятные стратегии и др.).
Литература:
- Власов Д. А. Информационные технологии в системе математической подготовки бакалавров: опыт МГГУ им. М. А. Шолохова / Информатика и образование. — 2012. — № 3. — С. 93–94.
- Власов Д. А. Реализация метода дерева решений в моделировании процесса принятия решений // Вопросы экономики и управления. — 2016. — № 2 (4). — С. 34–37.
- Власов Д. А. Ретроспективный анализ развития методов и моделей теории игр // Инновационная наука. — 2016. — № 8–1. — С. 42–43.
- Власов Д. А. Экономические риски: содержательный и методические аспекты // Инновационная наука. — 2016. — № 8–1. — С. 40–42.
- Власов Д. А., Монахов Н. В., Монахов В. М. Математические модели и методы внутримодельных исследований. — М.: Издательство МГГУ им. М. А. Шолохова, 2007. — 345 с.
- Власов Д. А. Методологические аспекты принятия решений // Молодой ученый. — 2016. — № 4. — С. 760–763.
- Моргенштерн О., Нейман Дж. Теория игр и экономическое поведение. — М.: Книга по Требованию, 2012. — 708 с.
- Портер М. Конкурентная стратегия. Методика анализа отраслей конкурентов. М.: Альпина Паблишер, 2011. — 454 с.
Ключевые слова
стратегия, конкуренция, равновесие, теоретико-игровая модель, платежная функция, оптимизационный подход, рынок сбыта продукции, матрица игрыПохожие статьи
Методы (методика) расширения рынков сбыта в условиях...
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Стратегия и тактика выхода компании на внешние рынки
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция.
Конкуренция и ключевые этапы её развития в процессе эволюции...
Теоретико-игровая модель конкурентной борьбы за рынки... В центре внимания статьи — построение и направления исследования теоретико-игровой модели конкурентной борьбы за рынки сбыта продукции.
Создание и использование программы для статистического...
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Методические подходы конкурентоспособности продукции
Конкурентоспособность продукции на рынке обеспечивается ее качеством.
Качество продукции и услуг всегда являлось одним из основных факторов конкурентной борьбы на национальных и мировом рынках, символом процветания отдельных предприятий, регионов и...
Теория игр: основные понятия, типы игр, примеры
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Статьи по ключевому слову "оптимизационный подход..."
"оптимизационный подход": Вопросы экономики и управления №5 (7) ноябрь 2016 г. — Власов Д. А. Теоретико-игровая модель конкурентной борьбы за рынки сбыта продукции.
Анализ конкурентной стратегии М. Портера — абсолютное...
Теоретико-игровая модель конкурентной борьбы за рынки... Существенное значение в конкурентной борьбе приобретает множество стратегий поведения субъектов конкурентного соперничества [7], (стратегия сохранения, стратегия вытеснения конкурента с рынка сбыта...
Похожие статьи
Методы (методика) расширения рынков сбыта в условиях...
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Стратегия и тактика выхода компании на внешние рынки
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция.
Конкуренция и ключевые этапы её развития в процессе эволюции...
Теоретико-игровая модель конкурентной борьбы за рынки... В центре внимания статьи — построение и направления исследования теоретико-игровой модели конкурентной борьбы за рынки сбыта продукции.
Создание и использование программы для статистического...
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Методические подходы конкурентоспособности продукции
Конкурентоспособность продукции на рынке обеспечивается ее качеством.
Качество продукции и услуг всегда являлось одним из основных факторов конкурентной борьбы на национальных и мировом рынках, символом процветания отдельных предприятий, регионов и...
Теория игр: основные понятия, типы игр, примеры
Теоретико-игровая модель конкурентной борьбы за рынки сбыта... Ключевые слова: теоретико-игровая модель, конкуренция, рынок сбыта продукции, матрица игры, платежная функция, оптимизационный подход, стратегия, равновесие.
Статьи по ключевому слову "оптимизационный подход..."
"оптимизационный подход": Вопросы экономики и управления №5 (7) ноябрь 2016 г. — Власов Д. А. Теоретико-игровая модель конкурентной борьбы за рынки сбыта продукции.
Анализ конкурентной стратегии М. Портера — абсолютное...
Теоретико-игровая модель конкурентной борьбы за рынки... Существенное значение в конкурентной борьбе приобретает множество стратегий поведения субъектов конкурентного соперничества [7], (стратегия сохранения, стратегия вытеснения конкурента с рынка сбыта...







