Особенности вычисления площадей по карте при выполнении практических работ по топографии
Автор: Гакаев Рустам Анурбекович
Рубрика: Методика преподавания учебных дисциплин
Опубликовано в Педагогика высшей школы №2 (5) июль 2016 г.
Дата публикации: 08.07.2016
Статья просмотрена: 2709 раз
Библиографическое описание:
Гакаев, Р. А. Особенности вычисления площадей по карте при выполнении практических работ по топографии / Р. А. Гакаев. — Текст : непосредственный // Педагогика высшей школы. — 2016. — № 2 (5). — URL: https://moluch.ru/th/3/archive/32/1158/ (дата обращения: 27.04.2024).
Суть практических работ по топографии заключается в том, что студенты, изучив теоретический материал, выполняют практические задания по формированию соответствующих умений и навыков работы с топографической картой. Часть практических работ выполняется индивидуальными заданиями: ориентирование, определение направлений движения по заданным азимутам, составление плана местности, определение относительной высоты холма, скорости течения реки, измерение длин линий по прямой и кривой и др. Практические работы с топографическими картами формируют навыки сложного чтения карты, позволяют, в будущем, анализировать географические явления, составлять физико-географические и экономико-географические характеристики отдельных участков или районов, давать оценку территории по заданным критериям [1, 2].
Определение площади карты и плана, как и отдельных контуров на нем имеет практическое значение. В результате вычисления площадей составляется экспликация угодий (перечень угодий с указанием их площади), производится организация территории и решается ряд других задач. Площади вычисляются различными способами.
Аналитический метод состоит в определении площади участка по результатам непосредственных измерений линий и углов в натуре или по координатам вершин (граничных точек). Точность величины площади участка при этом зависит только от ошибок измерения длин и углов на местности и характеризуется относительной ошибкой 1/500–1/1000. Однако в условиях большой контурности и вкрапливаний одних контуров в другие, площади которых определяются менее точными способами, аналитический метод становится нецелесообразен.
Аналитический способ основан на использовании результатов полевых измерении (длин линий и углов) и является наиболее точным. При этом используются формулы геометрии, тригонометрии и аналитической геометрии.
Графический метод заключается в том, что данные для вычисления площадей берутся с плана, графически, и площади отдельных геометрических фигур вычисляются с помощью геометрических формул. При графическом способе участок разбивают на треугольники, трапеции и другие фигуры, площадь которых можно вычислить, используя формулы геометрии. Для того чтобы повысить точность вычислений и избежать возможных грубых ошибок, площадь каждой фигуры вычисляют дважды и затем берут среднее (у треугольников разные стороны принимают за основания и к ним проводят высоты). Расхождения между результатами не должны превышать 1/100 (1 %) от площади вычисляемой фигуры.
Расстояния на плане определяются масштабной линейкой или выверенными линейками со скошенными краями. Точность таких измерений должна быть не ниже 2 мм. Точность определения линий на плане прямо пропорциональна их длине, так как короткие и длинные линии вычисляют с одной и той же абсолютной ошибкой (0,2 мм).
Если участок представляет собой многоугольник, то его делят на треугольники, прямоугольники или трапеции. С помощью измерителя и масштабной линейки определяют те величины, которые нужны для получения площадей отдельных фигур. Сумма площадей элементарных геометрических фигур даст общую площадь участка.
Точность определения площади графическим способом зависит от графической ошибки измерения отрезка на плане. Отрезок на плане циркулем — измерителем определяется с ошибкой +0,1 мм, которая не зависит от длины линии. Из этого следует, что относительная ошибка короткой линии больше, а длинной — меньше.
Правила для определения площади графическим способом:
- Площади определяются дважды (либо участок разбивается на другие элементарные фигуры, либо в треугольниках изменяются основания и высота).
- План берется в наиболее крупном масштабе.
- Фигуры должны быть как можно крупнее и не очень вытянуты, то есть основание и высота должны быть примерно равны.
- Если в геометрических фигурах есть линии, величины которых известны из непосредственных измерений, то их надо использовать для вычисления площадей.
- Предельное расхождение двукратных определений не должно превышать1:200 величины площади участка.
При работе по этому способу применяют специальные палетки для проведения высот.
Графически вычисляют площади контуров имеющих вытянутую форму (дорога, канал, ручей и т. д.), ширина которых не всегда выражается в масштабе плана, но она должна быть известна или подписана на плане.
Определение площадей палетками (механический способ). Для определения площадей небольших участков (обременения и сервитутов) по топографическим планам и картам применяют квадратные и параллельные прямоугольные палетки.
Квадратная палетка. Квадратная палетка представляет собой прозрачный лист целлулоида, стекла или восковки, на котором нанесена сеть квадратов со сторонами от 1 до 10 мм. Зная сторону квадрата, легко подсчитать площадь его применительно к любому масштабу плана. Для определения площади палетку накладывают на контур ABCD, имеющийся на плане. Вначале подсчитывают число полных квадратов, а затем неполные квадраты объединяют и глазомерно заменяют некоторым числом полных. Пусть таких квадратов девять. Произведение площади одного квадрата на число их даст площадь определяемого участка. Например, в криволинейном контуре на плане масштаба 1: 500 оказалось 58,5 клеток палетки со стороной квадрата 2 мм. В одном квадрате содержится площадь в 1 м2, следовательно, площадь определяемого контура будет равна 1 м2 * 58,5 клеток = 58,5 м2. Для упрощения подсчетов проводят утолщение линии через 1 см, чтобы число целых клеток можно было подсчитать сразу группами (по 25 мм2). Точность определения площади квадратной палеткой не превышает 1:100.
Недостаток квадратной палетки заключается в том, что площади долей клеток оцениваются на глаз, а подсчет целых клеток может сопровождаться ошибками, поэтому не рекомендуется такой палеткой определять площади больше 2 см2 на плане. Отмеченных выше недостатков квадратной палетки не наблюдается при определении площадей параллельной палеткой, представляющей собой лист прозрачного материала, на котором нанесены параллельные линии, в основном через 2 мм одна от другой.
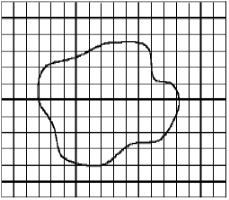
Рис. 1. Квадратная палетка
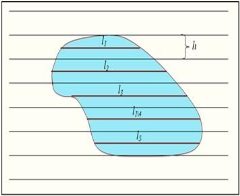
Рис. 2. Параллельная палетка
Палетки с параллельными линиями. Палетка с параллельными линиями отличается от квадратной тем, что вместо квадратов на ней наносятся параллельные линии. На ней нанесены параллельные линии с интервалом в 2 мм. Для определения площади участка палетку накладывают на контур плана так, чтобы наиболее удаленные друг от друга точки, например, приходились на середину расстояния между какими-либо параллельными линиями. В результате этого площадь определяемого контура будет разбита на трапеции, у которых сплошные линии будут средними линиями трапеций, а пунктирные (на палетке отсутствуют) — основаниями трапеций [3, 4].
Так как высоты трапеций одинаковы и заранее известны, то для получения площади контура надо измерить циркулем средние линии трапеций. Произведение суммы средних линий на расстояние между нитями даст общую площадь контура. При этом надо учитывать масштаб плана.
Чтобы не производить вычислений, ниже палетки наносят шкалу в виде простого линейного масштаба. Ее строят с учетом следующих соображений. При масштабе плана 1:10 000 расстоянию между нитями на палетке в 2 мм соответствует 20 м на местности, следовательно, каждому сантиметру длины полосы на плане будет в натуре соответствовать площадь в 0,2 га. Если на прямой отложить несколько отрезков по 1 см, сделать соответствующие подписи и один отрезок разделить на мелкие части, то достаточно к такой шкале приложить раствор циркуля, соответствующий сумме средних линий трапеций. Прочитанный отсчет по шкале даст площадь в гектарах.
Аналогично этому может быть построена шкала и для другого масштаба. Так, для масштаба 1: 25 000 целесообразно за основание шкалы взять отрезок в 0,8 см, что будет соответствовать 1 га.
Измерение площади участка с криволинейным контуром (криволинейная палетка). Объект с криволинейным контуром разбивают на геометрические фигуры, предварительно спрямив границы с таким расчетом, чтобы сумма отсеченных участков и сумма избытков взаимно компенсировали друг друга. Результаты измерений будут, в некоторой степени, приближенными.
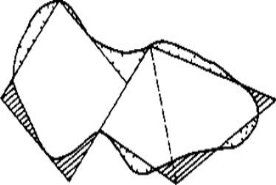
Рис. 3. Спрямление криволинейных границ участка и разбивка на простые геометрические фигуры
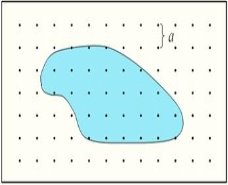
Рис. 4. Точечная палетка
Помимо квадратных палеток, применяют точечные палетки, представляющие собой прозрачные пластины с награвированными точками. Точки ставятся в одном из углов ячеек сеточной палетки с известной ценой деления, затем линии сетки удаляют. Вес каждой точки равен цене деления палетки. Площадь измеряемого участка определяют путем подсчета количества точек, оказавшихся внутри контура, и умножают это количество на вес точки [3, 4].
Измерение площадей значительных участков производится по картам с помощью планиметра. Планиметр служит для определения площадей механическим способом. Широкое распространение имеет полярный планиметр. Он состоит из двух рычагов — полюсного и обводного.

Рис. 5. Полярный планиметр
Определение площади контура планиметром сводится к следующим действиям. Закрепив полюс и установив иглу обводного рычага в начальной точке контура, берут отсчет. Затем обводной шпиль осторожно ведут по контуру до начальной точки и берут второй отсчет. Разность отсчетов даст площадь контура в делениях планиметра. Зная абсолютную цену деления планиметра, определяют площадь контура.
Литература:
- Гакаев Р. А. Статистические методы освоения географических дисциплин бакалавров по направлению подготовки «География». Педагогика высшей школы. 2015. № 2 (2). С. 31–35.
- Гакаев Р. А. Методы картографического исследования и этапы их формирования. Педагогика высшей школы. 2016. № 1 (4). С. 1–4.
- Гакаев Р. А. Точность и погрешность измерений на картах при выполнении практических работ по топографии. Педагогика высшей школы. 2016. № 1 (4). С. 48–53.
- Жмойдяк Р. А. и др. Лабораторные занятия по топографии с основами геодезии. Учебное пособие для географических факультетов / Р. А. Жмойдяк, В. Я. Крищанович, Б. А. Медведев / Мн.: Высш. школа, 1979. — 295 с., ил.
Похожие статьи
Совершенствование методов определения площади земельных...
В механическом способе площадь определяется с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану...
Точность и погрешность измерений на картах при выполнении...
Поперечный масштаб позволяет существенно повысить точность графических работ на планах и картах.
Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика, с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от...
Вычисление площадей фигур, изображенных на клетчатой бумаге
Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь.
План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Методы математического описания контуров лекал швейных...
Традиционно для математического описания контуров криволинейных участков лекал используются методы интерполяции и аппроксимации.
Для получения при аппроксимации более гладкой контурной линии может быть использован способ гладкой окружностной...
Применение ИКТ в геометрических и физических приложениях...
Ключевые слова: способ трапеций, способ средних прямоугольников, способ Симпсона, центр тяжести плоской фигуры, площадь криволинейной трапеции, MathCAD. Цель исследования: изучить понятие определённого интеграла и его приложений.
Изображение фигуры человека с учетом возможностей...
Для соблюдения единой линии горизонта (уровня зрения) и
— Кисти с параметром рисования фигурами. В таких графических редакторах, как
Имея большой набор кистей с фигурами в нескольких различных ракурсах, он быстро расставит их по площади, изменяя цвет, масштаб...
Численные методы для решения задачи о нахождении выпуклой...
Требуется найти выпуклую фигуру вращения максимальной площади поверхности
Построим начальный опорный план, методом минимальной стоимости, согласно которому, сперва заполним ячейки с минимальными затратами на...
Коэффициент формы как геометрическая характеристика
Для фигур с криволинейным контуром выражение (1) можно преобразовать к следующему виду
Требуется найти выпуклую фигуру вращения максимальной площади поверхности: (4). опорная функция , которой удовлетворяет условиям.
Похожие статьи
Совершенствование методов определения площади земельных...
В механическом способе площадь определяется с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану...
Точность и погрешность измерений на картах при выполнении...
Поперечный масштаб позволяет существенно повысить точность графических работ на планах и картах.
Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика, с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от...
Вычисление площадей фигур, изображенных на клетчатой бумаге
Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь.
План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).
Методы математического описания контуров лекал швейных...
Традиционно для математического описания контуров криволинейных участков лекал используются методы интерполяции и аппроксимации.
Для получения при аппроксимации более гладкой контурной линии может быть использован способ гладкой окружностной...
Применение ИКТ в геометрических и физических приложениях...
Ключевые слова: способ трапеций, способ средних прямоугольников, способ Симпсона, центр тяжести плоской фигуры, площадь криволинейной трапеции, MathCAD. Цель исследования: изучить понятие определённого интеграла и его приложений.
Изображение фигуры человека с учетом возможностей...
Для соблюдения единой линии горизонта (уровня зрения) и
— Кисти с параметром рисования фигурами. В таких графических редакторах, как
Имея большой набор кистей с фигурами в нескольких различных ракурсах, он быстро расставит их по площади, изменяя цвет, масштаб...
Численные методы для решения задачи о нахождении выпуклой...
Требуется найти выпуклую фигуру вращения максимальной площади поверхности
Построим начальный опорный план, методом минимальной стоимости, согласно которому, сперва заполним ячейки с минимальными затратами на...
Коэффициент формы как геометрическая характеристика
Для фигур с криволинейным контуром выражение (1) можно преобразовать к следующему виду
Требуется найти выпуклую фигуру вращения максимальной площади поверхности: (4). опорная функция , которой удовлетворяет условиям.







