Математическая модель процесса топливоподачи системой Common Rail с электро-гидравлической форсункой
Автор: Субботенко Дмитрий Игоревич
Рубрика: 5. Энергетика
Опубликовано в
Дата публикации: 05.04.2014
Статья просмотрена: 1831 раз
Библиографическое описание:
Субботенко, Д. И. Математическая модель процесса топливоподачи системой Common Rail с электро-гидравлической форсункой / Д. И. Субботенко. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы II Междунар. науч. конф. (г. Санкт-Петербург, апрель 2014 г.). — Т. 0. — Санкт-Петербург : Заневская площадь, 2014. — С. 58-60. — URL: https://moluch.ru/conf/tech/archive/89/5403/ (дата обращения: 26.04.2024).
Представлена математическая модель процесса топливоподачи системой CommonRail, включающей в себя электрогидравлическую форсунку. Методика расчета базируется на уравнении движения маловязких сортов топлива.
Ключевые слова:математическая модель, расчет, электрогидравлическая форсунка, дизель, топливоподача, Commonrail.
Аккумуляторные топливные системы (системы Common Rail), получившие свое распространение в последние 15-17 лет, находятся в процессе постоянного конструктивного совершенствования, технический уровень которых также определяется совершенствованием применяемых форсунок.
Для осуществления оптимизации процессов в топливной аппаратуре (ТА) дизеля с целью улучшения его экономических и экологический характеристик форсунки должны удовлетворять следующим параметрам [1]:
- стабильность работы при высоких давлениях;
- высокое быстродействие;
- возможность фиксированной величины цикловой подачи;
- малое энергопотребление и низкий расход топлива на управление.
Периодическое ужесточение экологических норм заставляет производителей оптимизировать не только топливный насос высокого давления, повышая тем самым давление впрыска, но и параметры форсунок.
Применение систем математического моделирования позволяет значительно сократить продолжительность и стоимость разработки элементов ТА. В математической модели впрыска топлива рассматривается электрогидравлическая форсунка с электромагнитным клапаном фирмы Busch. Принцип действия форсунки подробно изложен в [2].
Расчетная схема электромагнитной форсунки представлена на рис.1.
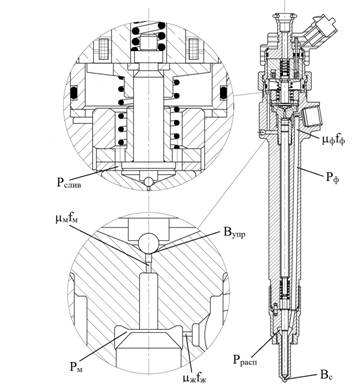
Рис. 1. Расчетная схема форсунки с электромагнитным управлением
Для описания физических процессов, происходящих в системе, с применением электрогидравлической форсунки приняты следующие допущения:
- плотность топлива и скорость звука постоянны;
- движение топлива в топливопроводе принимается одномерным;
- давление в аккумуляторе в начале каждого расчетного режима считается постоянным и равным остаточному давлению в системе;
- утечки в прецизионных соединениях и силы трения в зазорах прецизионных кинематических пар не учитываются;
- соударения подвижных деталей с упорами являются абсолютно неупругими и деформации деталей вследствие соударений отсутствуют;
- давление в акустически коротких объемах в текущий момент времени одинаково во всех точках.
Расчет топливной аппаратуры основан на решении уравнений теории гидравлического удара, разработанной Н.Е. Жуковским, и уравнений граничных условий у ТНВД и форсунки по методу профессора И. В. Астахова. Совершенствованию и уточнению методик для гидродинамического расчёта дизельных ТПС в большой мере способствовали работы отечественных учёных И. В. Астахова [3, 4, 5], Л. В. Грехова [2, 6, 7], Л. Н. Голубкова [8, 9], Ю. Я. Фомина [10,11], и др.
В изложенной методике часть положений теории представлены в виде конечных уравнений и формул. Движение топлива в нагнетательном трубопроводе при учете гидравлического сопротивления описывается дифференциальным уравнением, называемым “телеграфным”:
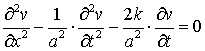 ,
,
где x и t – длина топливопровода и время, v–скорость топлива, k – фактор гидравлического сопротивления, a – скорость звука в топливе.
Если ввести функцию v(x, t) =p(x, t), то полученное уравнение допускает решения в следующем виде:
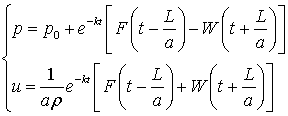
где p и v– давление топлива у форсунки;
p0 и v0 – начальные значения давления и скорости топлива в магистрали;
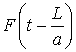 и
и 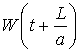 – прямая и обратная волны давления; затухание колебаний.
– прямая и обратная волны давления; затухание колебаний.
Уравнения баланса топлива в полостях традиционно записываются для формулировки граничных условий в задаче о трубопроводе. В качестве граничных условий для выражения (1) применяются уравнения объемных балансов. Для i-й камеры уравнение объемного баланса течения топлива:
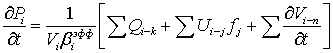
где 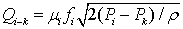 - перетечки в (из) k-ю полость, где Piи Pk – давление до и после характерного сечения, ρ- плотность топлива в характерном сечении; Vi– объем i-ой камеры; βiэфф – коэффициент характеризующий сжатия топлива и деформацию полости; Ui-j - скорость втекания топлива из (в) j-гo канала; dVj-n - изменение объема под действием перемещения n-го элемента;
- перетечки в (из) k-ю полость, где Piи Pk – давление до и после характерного сечения, ρ- плотность топлива в характерном сечении; Vi– объем i-ой камеры; βiэфф – коэффициент характеризующий сжатия топлива и деформацию полости; Ui-j - скорость втекания топлива из (в) j-гo канала; dVj-n - изменение объема под действием перемещения n-го элемента;
Граничные условия у электрогидравлической форсунки определяются исходя из уравнений объемных балансов и действующих сил с учетом сжимаемости топлива и упругости подвижных элементов, описываются следующими уравнениями:
граничные условия для входной полости форсунки со штуцером и фильтром
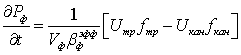 ;
;
граничные условия в полости мультипликатора форсунки
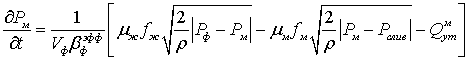 ;
;
граничные условия в распылителе перед сопловыми отверстиями
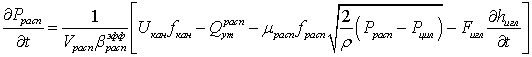 ;
;
расход топлива на управление
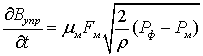 ;
;
расход топлива через распыливающие отверстия
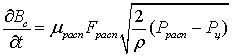 ;
;
где α – коэффициент сжимаемости топлива, Pф - давление в полости форсунки, Pрасп -давление в области распылителя, Pм-давление в полости мультипликатора, Pц -давление в цилиндре двигателя, Pслив- давление за мультипликатором в сливной полости, Uкан - скорость течения топлива в канале форсунки, Uтр- скорость течения топлива в трубопроводе, fкан -площадь поперечного сечения канала, fтр- площадь поперечного сечения трубопровода, fигл - площадь поперечного сечения иглы форсунки, Qутрасп- утечки топлива через распылитель, Qутм- утечки топлива через мультипликатор, µфfф -эффективная площадь проходного сечения форсунки, µраспfрасп -эффективная площадь проходного сечения распылителя, µжfж -эффективная площадь проходного сечения жиклера перед мультипликатором, µмfм -эффективная площадь проходного сечения мультипликатора, ρ- плотность топлива, 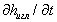 -скорость подъема иглы, Bупр - расход топлива на управление, Bс - расход топлива через распыливающие отверстия.
-скорость подъема иглы, Bупр - расход топлива на управление, Bс - расход топлива через распыливающие отверстия.
Разработанная математическая модель электрогидравлической форсунки аккумуляторной топливной системы Common Rail позволяет производить проектирование электрогидравлической форсунки, изучать влияние конструктивных параметров на процесс впрыскивания топлива, проводить расчетную адаптацию топливной системы к проектируемому двигателю.
Литература:
1. Robert Bosch GmbH, Dieselmotor-Management, 3. vollständige überarbeitete und erweiterte Auflage, 2002. – S. 443.
2. Грехов Л.В. Топливная аппаратура и системы управления дизелей: Учебник для ВУЗов. / Л.В. Грехов, Н.А. Иващенко, В.А. Марков – М.: Легион-Автодата, 2004. – 344 с.
3. 3.Астахов А.В. Топливные системы и экономичность дизелей / А.В. Астахов, Л.Н. Голубков, В.И. Трусов, А.С. Хачиян, Л.М. Рябикин. - М.: Машиностроение, 1990.-288 с.
4. Астахов И.В. Расчет конца процесса впрыска топлива в быстроходных дизелях с учетом гидравлического сопротивления и следа волн давления / И.В. Астахов, Л.А. Илиев // Известия вузов. Машиностроение. — 1970. - №10. - С. 103-110.
5. Астахов И.В. Характер износа запирающих конусов распылителя / И.В. Астахов, Г.С. Корнилов, В.М. Гундоров // Двигателестроение. - 1987. - №9. — С. 26-28.
6. Грехов Л.В. Улучшение показателей топливной аппаратуры дизелей аккумулированием утечек в надыгольном объеме форсунок. Рабочие процессы дизелей: Учебное пособие. / Л.В. Грехов — Барнаул: Изд-во АлтГТУ. - 1995. - С. 47-56.
7. Грехов Л.В. Уточненная математическая модель процесса подачи топлива в дизеле / Л.В. Грехов // Известия вузов. Машиностроение. - 1997. — № 10-12. — С. 47-51.
8. Голубков Л.Н. Алгоритмы и программы расчета топливных систем на Фортране: Учебное пособие. / Л.Н. Голубков - М.: МАДИ, 1980. - 40 с.
9. Голубков Л.Н. Гидродинамические процессы в топливных системах дизелей при двухфазном состоянии топлива /Л.Н. Голубков // Двигателестроение. — 1987.-№1.-С.32-35.
10. Фомин Ю.Я. Топливная аппаратура судовых дизелей. / Ю.Я. Фомин - М.: Транспорт, 1966. - 240 с.
11. Фомин Ю.Я., Никонов Г.В., Ивановский В.Г. Топливная аппаратура дизелей: Справочник./ Ю.Я. Фомин, Г.В. Никонов, В.Г. Ивановский - М.: Машиностроение, 1982. - 168 с.
Ключевые слова
расчет, математическая модель, дизель, электрогидравлическая форсунка, топливопо-дача, Аккумуляторная топливная система, Common railПохожие статьи
Ремонт топливопроводов высокого давления топливной...
электрогидравлическая форсунка, расход топлива, гидравлическое сопротивление, давление, движение топлива, система, скорость звука, скорость топлива, топливная аппаратура.
Разработка канолопромывочной головки | Статья в журнале...
электрогидравлическая форсунка, расход топлива, гидравлическое сопротивление, давление, движение топлива, система, скорость звука, скорость топлива, топливная аппаратура.
Анализ оборудования, применяемого для диагностики, испытания...
высокое давление, топливная система, расход топлива, топливная аппаратура, топливопровод, топливный насос, внутренний диаметр, мобильная техника, гидравлическое сопротивление, уплотнительный конус.
Влияние воды на изнашивание топливной аппаратуры
Ключевые слова: форсунка, топливо, давление впрыска, расход топлива, диагностика, испытание, гидравлическая плотность. Форсунка дизельного двигателя внутреннего сгорания служит связующим элементом между насосом высокого давления...
Новое видение процесса распыливания жидкого топлива в дизеле
Стрелкой показано направление движения струи топлива. Топливо проходит сопловой канал с большой скоростью, сужается, происходит местное понижение давления и возникают пузырьки газа (обозначены кругляшками).
Компьютерное моделирование гидравлических систем
Гидравлическая система летательных аппаратов: вертолета... Понятие гидравлического привода (гидравлической системы).
В математической модели впрыска топлива рассматривается электрогидравлическая форсунка с.
Современные дизельные двигатели. Топливная система
высокое давление, топливная система, расход топлива, топливная аппаратура, топливопровод, топливный насос, внутренний диаметр, мобильная техника, гидравлическое сопротивление, уплотнительный конус.
Расчёт предпомпажных состояний газотурбинной установки
Гидравлическая система летательных аппаратов: вертолета...
Скорость газа в критическом сечении сопла, м/с. Рис. 3. График изменения удельной тяги и удельного расхода топлива от скорости полета летательного аппарата.
Система управления расходованием топлива
Дроссель изменяет соотношение компонентов расхода топлива в соответствии с командами системы управления.
Это позволяет повысить эффективность применения системы в условиях, когда существенно ограничивается диапазон изменения давления в камере сгорания.
Похожие статьи
Ремонт топливопроводов высокого давления топливной...
электрогидравлическая форсунка, расход топлива, гидравлическое сопротивление, давление, движение топлива, система, скорость звука, скорость топлива, топливная аппаратура.
Разработка канолопромывочной головки | Статья в журнале...
электрогидравлическая форсунка, расход топлива, гидравлическое сопротивление, давление, движение топлива, система, скорость звука, скорость топлива, топливная аппаратура.
Анализ оборудования, применяемого для диагностики, испытания...
высокое давление, топливная система, расход топлива, топливная аппаратура, топливопровод, топливный насос, внутренний диаметр, мобильная техника, гидравлическое сопротивление, уплотнительный конус.
Влияние воды на изнашивание топливной аппаратуры
Ключевые слова: форсунка, топливо, давление впрыска, расход топлива, диагностика, испытание, гидравлическая плотность. Форсунка дизельного двигателя внутреннего сгорания служит связующим элементом между насосом высокого давления...
Новое видение процесса распыливания жидкого топлива в дизеле
Стрелкой показано направление движения струи топлива. Топливо проходит сопловой канал с большой скоростью, сужается, происходит местное понижение давления и возникают пузырьки газа (обозначены кругляшками).
Компьютерное моделирование гидравлических систем
Гидравлическая система летательных аппаратов: вертолета... Понятие гидравлического привода (гидравлической системы).
В математической модели впрыска топлива рассматривается электрогидравлическая форсунка с.
Современные дизельные двигатели. Топливная система
высокое давление, топливная система, расход топлива, топливная аппаратура, топливопровод, топливный насос, внутренний диаметр, мобильная техника, гидравлическое сопротивление, уплотнительный конус.
Расчёт предпомпажных состояний газотурбинной установки
Гидравлическая система летательных аппаратов: вертолета...
Скорость газа в критическом сечении сопла, м/с. Рис. 3. График изменения удельной тяги и удельного расхода топлива от скорости полета летательного аппарата.
Система управления расходованием топлива
Дроссель изменяет соотношение компонентов расхода топлива в соответствии с командами системы управления.
Это позволяет повысить эффективность применения системы в условиях, когда существенно ограничивается диапазон изменения давления в камере сгорания.











