О возможности применения системного подхода к проблеме управления движением судов
Автор: Тюфанова Анастасия Александровна
Рубрика: 9. Транспорт
Опубликовано в
III международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2016)
Дата публикации: 10.03.2016
Статья просмотрена: 77 раз
Библиографическое описание:
Тюфанова, А. А. О возможности применения системного подхода к проблеме управления движением судов / А. А. Тюфанова. — Текст : непосредственный // Технические науки: теория и практика : материалы III Междунар. науч. конф. (г. Чита, апрель 2016 г.). — Чита : Издательство Молодой ученый, 2016. — С. 118-121. — URL: https://moluch.ru/conf/tech/archive/165/9980/ (дата обращения: 26.04.2024).
Рассмотрен процесс движения судов в зоне обслуживания системы управления движением судов с точки зрения системного анализа.
Ключевые слова: судопоток, судно, система, водный путь.
Методы управления движением судов остаются наименее исследованными в теории судопотока. В этом случае наиболее перспективной следует считать методологию системного анализа. Термин "система" имеет множество определений, но в рассматриваемом контексте под системой понимается "множество элементов" вместе со связями между элементами и между их признаками. Элементы — неделимые части или компоненты системы, определяющие ее состав [1]. При необходимости вводится иерархия подсистем. Признаки отражают самые разнообразные свойства элементов и подсистем, а связи объединяют систему в единое целое, придавая ей два таких важных макроскопических качества, как обособленность и целостность. В сущности, система становится таковой лишь благодаря наличию многих видов связи между подсистемами, между элементами и между признаками подсистем и элементов. Не раскрывая всего многообразия связей, выделим их в три основные группы:
характеристические связи, определяющие соотношения между признаками подсистем и элементов, например, зависимость между скоростью и интенсивностью судопотока;
информационные связи, определяющие пути передачи информации внутри системы;
управляющие (функциональные) связи или воздействия, генерируемые человеком для достижения какой-либо частной цели.
Исходя из этих общих положений, процесс движения судов в зоне обслуживания системы управления движением судов (СУДС) можно рассматривать как функционирование сложной (большой) системы, состоящей из трех систем "водный путь — судопоток — СУДС".
В принципе, система "водный путь" аналогично понятию "естественное окружение", применяемому в системном анализе. Однако в данном случае целесообразно использовать именно понятие "система", поскольку элементы водного пути имеют характеристические, информационные и управляющие связи с другими системами, формирующими сложную систему, которая не просто существует в данном окружении, но и функционирует с учетом признаком элементов водного пути [2].
Среди элементов системы "водный путь" можно выделить акваторию (признаки: размеры, форма, глубины), навигационную обстановку (наличие и характеристики средств навигационного обеспечения, естественные ориентиры), гидрометеорологические условия (наличие течения, ветра, волнения). Особо следует отметить, что система "водный путь" почти всегда имеет общую с СУДС подсистему в виде схемы движения, включающей в себя также такие элементы, как фарватеры, зоны и линии разделения движения, специальные районы плавания. Такие элементы, формируя часть топологической структуры системы "водный путь", являются первичными элементами СУДС, которые определяют пространственное распределение судопотоков, выбор скорости движения, т. е. в сущности, оказывают на суда управляющее воздействия. Структурирование системы "водный путь" и определение признаков и связей между ее элементами особых трудностей не вызывает.
Второй составляющей данной сложной системы, с которой связаны основные цели системного анализа, является система "судопоток". Состав этой подсистемы однороден: он включает в себя лишь суда, хотя спектр признаков судов весьма широк как по количественному, так и по качественному разнообразию. Особенность признаков судов заключается в том, что им приписывается различный характер в зависимости от подхода: макроскопического или микроскопического. Например, техническая скорость при микроскопическом подходе, когда рассматривается конкретное судно в отдельности, имеет строго детерминистическое определение, т. е., она функционально зависит от размеров и формы корпуса судна, мощности главного двигателя, загрузки и т.п. Однако при макроскопическом подходе, когда речь идет о системе "судопоток" в целом, техническая скорость любого судна — это случайная величина, которая задается некоторой функцией распределения. Иногда для изучения проблемы на более высоком уровне целесообразно судно представлять в виде подсистемы "судоводитель — средства управления — судно как объект управления".
Судопотоку присущи также интегральные признаки, которыми не обладают отдельные суда: интенсивность, плотность и средняя скорость. Именно целенаправленное изменение этих признаков преследуется при воздействии на суда со стороны СУДС.
Характерной особенностью наблюдаемого судопотока в портах является то, что с большей вероятностью в течение некоторого заданного промежутка времени в порт поступят все суда, приход которых ожидается для погрузки или выгрузки определенного вида груза, и практически с нулевой вероятностью поступит большее, чем ожидается. Исходя из этого определяющего условия, попытаемся построить модель управляемого судопотока [1].
Пусть, в порту на интервале (О, Т) планируется N≥1 судозаходов (для погрузки или выгрузки одного какого-либо рода груза). Подход судов в порт предполагается случайным, причем интервалы между любыми двумя соседними судозаходами считаются случайными величинами, подчиненными одному и тому же закону распределения:
А(t), A(+0)<1, А(t), A(+0)<1,
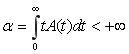
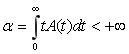 .
.
Основными вероятностными характеристиками описанного потока наряду с функцией распределения (ф.р.) А(t) служит распределение вероятностей числа поступивших в интервале (О, Т) судов [3]:
![]()
![]()
и ф.р. случайного промежутка времени до наступления N-ого судозахода, которое обозначим ξN.
Введенный случайный поток, определенный для 0 ≤ t ≤+ ∞, будем называть ограниченным рекуррентным потоком (ОРП).
Вероятности πi(t) легко находятся с помощью методов теории восстановления. Пусть процесс поступления судов начинается в момент t=0.
![]()
где А(i)(t) — i-кратная свертка ф.р. А(t) с собой; А(0)(t)=0.
Нетрудно также убедиться, что Р {ξN < t} = πN(t).
Для решения рассматриваемой задачи кажется естественным использовать модель так называемого потока Бернулли, для которого:
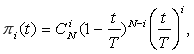 0
0![]() i
i![]() N, 0
N, 0![]() t
t![]() τ.
τ.
Однако то обстоятельство, что эта модель предполагает с вероятностью единица приход в промежутке [O,T] точно N судов, ограничивает возможность ее использования для описания потока морских судов. На практике вероятность упомянутого события хотя и близка к единице, но все же отлична от нее. Отметим попутно, что поток Бернулли не является ОРП, так как в этом потоке интервалы между соседними наступлениями событий статистически зависимы между собой, причем время до наступления каждого из N событий распределено равномерно в промежутке [O,T] и моменты их наступлений совершенно между собой не согласованы.
Довольно часто на практике приходится сталкиваться с проблемой наложения (или суперпозиций) нескольких потоков судов. Вообще говоря, результирующий поток имеет значительно более сложную структуру, чем составляющие потоки, если последние достаточно просты. Хорошо известно, к примеру, что поток, образованный наложением любого конечного числа m>1 независимых простейших потоков с параметрами λ1, …, λm, также является простейшим потоком с параметрами λ1+…+ λm [3].
Ограниченные пуассоновские потоки аналогичным свойством уже не обладают.
Мы рассмотрели несколько упрощенную ситуацию, при которой в интервале (О,Т) могли поступать только суда, включенные в план этого периода. Приведенная модель судопотока является достаточно правдоподобной только на промежутке, поскольку на следующем плановом промежутке будут поступать уже другие суда и с положительной вероятностью возможно наложение потока судов, не поступивших в первом интервале (из числа запланированных), и нового потока судов, приход которых запланирован во втором интервале. Новый поток судов характеризуется другой функцией распределения А(t) и другим значением N. Поэтому возникает необходимость в изучении потока, образованного наложением потоков судов на двух соседних плановых промежутках. В реальных условиях всегда достаточно рассматривать эффект наложения судопотоков только на двух смежных плановых промежутках. Обычно число судов "переходящих" из первого промежутка на второй не превышает трех — четырех [2].
Наиболее сложной в структурном отношении в рассматриваемой сложной системе является СУДС. В структурно-функциональном отношении СУДС представляется тремя основными подсистемами: "персонал", "технические средства" и "схема движения". При изучении элементов этих подсистем, их признаков и связей возникают наиболее сложные проблемы, связанные с организационными, техническими, технологическими, психофизиологическими и социально-экономическими аспектами.
Моделирование сложной системы преследует несколько целей, каждая из которых может быть выражена некоторыми критериями, причем такие критерии не всегда согласуются между собой и противоречивы. В итоге можно сформировать или интегральный (обобщенный) критерий или систему критериев, которая бы являлась основой для выбора оптимального (по данной системе критериев) варианта модели системы из нескольких альтернатив. Так, применительно к системе "водный путь — судопоток — СУДС" интегральный критерий может соответствовать такой цели, как "достижение заданного уровня безопасности движения судов при минимальных затратах".
Общий подход к принятию решения может быть сведен к следующему:
имеется некоторый набор альтернатив (вариантов) модели системы А, причем каждая альтернатива ![]() характеризуется совокупностью интегральных признаков n подсистем ain, где n — количество подсистем, i — количество интегральных признаков;
характеризуется совокупностью интегральных признаков n подсистем ain, где n — количество подсистем, i — количество интегральных признаков;
имеется совокупность критериев ![]() , отражающих количественно множество признаков подсистем, т. е., каждая альтернатива характеризуется вектором
, отражающих количественно множество признаков подсистем, т. е., каждая альтернатива характеризуется вектором ![]() ;
;
необходимо принять решение о выборе одной из альтернатив или по одному критерию (простое решение) или по совокупности критериев (сложное решение).
Эта задача сводится к нахождению оператора (отображения) φ, который каждому вектору ![]() ставит в соответствие действительное число
ставит в соответствие действительное число ![]() , определяющее степень предпочтительности выбранного варианта (здесь φ — интегральный критерий).
, определяющее степень предпочтительности выбранного варианта (здесь φ — интегральный критерий).
Таким образом, проблему безопасного и эффективного управления движением судов в зонах действия СУДС целесообразно решать на основе методологии системного анализа с привлечением математического аппарата исследования операций.
Литература:
- Каштанов, В.А. Теория надежности сложных систем/В.А. Каштанов, А.И. Медведев/– М.:ФИЗМАТЛИТ, 2010. — 608 с.
- Лентарев, А. А. Морские районы систем обеспечения безопасности мореплавания// Владивосток: Морской государственный университет, 2004. — 114 с.
- Тюфанова, А.А. Роль математического моделирования управляемого потока судов в безопасности мореплавания в портовых водах// Сборник научных трудов, выпуск № 12. Новороссийск РИО "МГА им.адм. Ф.Ф.Ушакова", 2007. — с.23-25
Похожие статьи
Системный анализ как новое направление исследования...
- анализ системы управления предприятием; - анализ форм отношений документов существующих на предприятии, на маршрутах их движения и технологии обработки.
Зависимость дальности обнаружения целей радиолокационных...
В статье на примере системы управления движения судов (СУДС) порта Новороссийск проведен анализ и расчет дальности обнаружения целей береговыми радиолокационными станциями под воздействием метеорологических условий для нескольких типов эталонных...
Анализ надежности Центра системы управления движением...
В статье рассмотрен процесс функционирования системы управления движением судов.
Ключевые слова: надежность, система управления движением судов, многоканальная система массового обслуживания, безотказная работа.
Применение метода многопараметрического распознавания...
Рассмотрено применение метода многопараметрического распознавания образов для диагностики технического состояния радиорелейного оборудования «Ericsson MiniLink-7Е» системы управления движением судов.
Применение генератора колебаний с хаотической несущей...
Основными видами технических средств системы управления движением судов (СУДС), обеспечивающих получение информации о состоянии акватории, навигационной обстановке и судах в районе действия СУДС...
Факторы, влияющие на эксплуатационную надежность технических...
Система управления движением судов (СУДС) в РФ является неотъемлемой частью Государственной системы обеспечения безопасности мореплавания, создается и действует на акваториях морских портов, во внутренних водах...
Разработка рекомендаций по формированию автоматизированной...
В статье предлагаются пошаговые рекомендации по формированию автоматизированной системы управления дорожным движением в г. Волгограде. Раскрыто понятие единой диспетчерской службы и ее основные задачи.
Математическая модель анализа эксплуатационной надежности...
Действующие системы управления движением судов (СУДС) являются восстанавливаемыми, резервированными, дублированными, частично обслуживаемыми, длительного непрерывного действия, с круглосуточным режимом работы.
Дефекты программного обеспечения системы управления...
Ключевые слова: дефект, программное обеспечение, отказ, система управления движением судов.
Различают два основных уровня, на которых происходит диагностика структуры ПО: анализ исходного и бинарного (исполняемого) кодов.
Похожие статьи
Системный анализ как новое направление исследования...
- анализ системы управления предприятием; - анализ форм отношений документов существующих на предприятии, на маршрутах их движения и технологии обработки.
Зависимость дальности обнаружения целей радиолокационных...
В статье на примере системы управления движения судов (СУДС) порта Новороссийск проведен анализ и расчет дальности обнаружения целей береговыми радиолокационными станциями под воздействием метеорологических условий для нескольких типов эталонных...
Анализ надежности Центра системы управления движением...
В статье рассмотрен процесс функционирования системы управления движением судов.
Ключевые слова: надежность, система управления движением судов, многоканальная система массового обслуживания, безотказная работа.
Применение метода многопараметрического распознавания...
Рассмотрено применение метода многопараметрического распознавания образов для диагностики технического состояния радиорелейного оборудования «Ericsson MiniLink-7Е» системы управления движением судов.
Применение генератора колебаний с хаотической несущей...
Основными видами технических средств системы управления движением судов (СУДС), обеспечивающих получение информации о состоянии акватории, навигационной обстановке и судах в районе действия СУДС...
Факторы, влияющие на эксплуатационную надежность технических...
Система управления движением судов (СУДС) в РФ является неотъемлемой частью Государственной системы обеспечения безопасности мореплавания, создается и действует на акваториях морских портов, во внутренних водах...
Разработка рекомендаций по формированию автоматизированной...
В статье предлагаются пошаговые рекомендации по формированию автоматизированной системы управления дорожным движением в г. Волгограде. Раскрыто понятие единой диспетчерской службы и ее основные задачи.
Математическая модель анализа эксплуатационной надежности...
Действующие системы управления движением судов (СУДС) являются восстанавливаемыми, резервированными, дублированными, частично обслуживаемыми, длительного непрерывного действия, с круглосуточным режимом работы.
Дефекты программного обеспечения системы управления...
Ключевые слова: дефект, программное обеспечение, отказ, система управления движением судов.
Различают два основных уровня, на которых происходит диагностика структуры ПО: анализ исходного и бинарного (исполняемого) кодов.











