Исследование нелинейной динамической цепи с диодными элементами в системе электроснабжения

В статье приведено решение дифференциальных уравнений состояния нелинейной динамической цепи численным методом и рассмотрен переходной процесс с помощью виртуальной компьютерной модели.

The solution of the differential equations of a condition of a nonlinear dynamic chain by a numerical method is provided in article and process by means of virtual computer model is considered transitional.

Нелинейные динамические цепи, в связи с разработкой на их основе надежных высококачественных устройств, находят широкое применение в различных областях автоматики, радиоэлектроники, вычислительной техники и электроснабжения. При этом используются неавтономные нелинейные динамические цепи с диодом, активным сопротивлением и емкостью. При разработке систем управления для устройств автоматики могут быть применены различные схемные решения. Рассмотрим цепь, состоящую из резисторов, диода и емкости собранную по смещенной схеме (рис 1.,а).

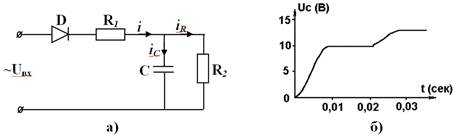
Рис. 1. Цепь последовательно соединенных диода Д, активного сопротивления R₁, R₂ емкости С (а) и кривая изменения напряжения на емкости в зависимости от времени (б)

Настоящее время широко применяются различные методы анализа таких цепей. Нами для этой цепи предлагается использовать численные решения уравнений состояния цепи методом Эйлера. При этом необходимо определить на некотором отрезке приближенное решение уравнения:

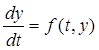
Принимаем характеристику диода идеальной и допускаем, что 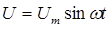. Тогда для состояния диода имеет следующее уравнение:

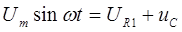                                                                                         (1)

Если

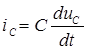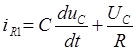;                                                                              (2)

Из (1) имеем

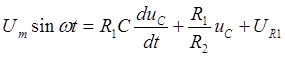
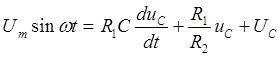
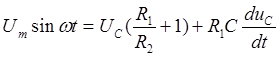
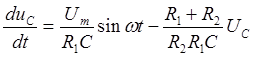
где: 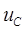- напряжение на емкости.

Решение уравнения (2) по Эйлеру выглядит следующим образом:

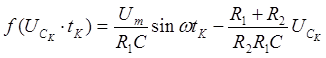
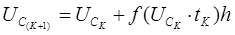                                                                            (3)

Здесь

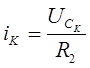                                                                                                                (4)

где: k=0, 1, 2, …; h — шаг интегрирования.

До момента t=t₁ напряжение на емкости определяется по (3) с нулевым начальным условием. С момента t’=t₁ происходит размыкание диода и до момента t₂ напряжение на емкости остается на уровне напряжения для момента t₁, с момента t₃ диод снова открывается и напряжение на емкости снова описывается зависимостью (3) с другим начальным условием.

На рис. 1.,б показана кривая изменения напряжения на емкости, получен-ная решением уравнения (3) на ЭВМ. При этом принятие U_m=100 В, R=300 Ом, С=200 мкФ.

На рис. 2.а, показаны зависимости изменения напряжения на емкости от времени при различных значениях величины активного сопротивления R. Как видно из рисунка, изменение величины активного сопротивления R приводит к изменению времени заряда конденсатора.

Таким образом, изменением параметров цепи можно регулировать время, установившееся напряжением на емкости и его величиной.

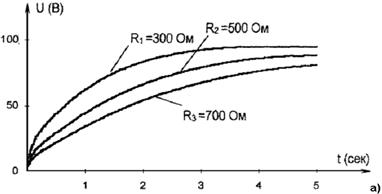
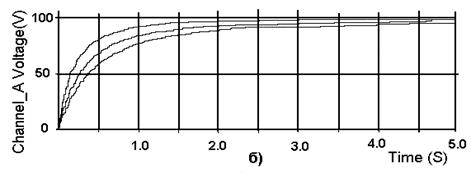
Рис. 2. Кривые изменения напряжения на емкости от времени при различных значениях величины сопротивления R (а) и виртуально-экспериментальные (б)

На рис.2.б. показаны эти же кривые, полученные виртуально-экспериментальными исследованиями (на базе системы схемотехнического моделирования «МS-01»). Сравнение рис.2.а и рис.2.б показывает их незначительное различие, которое объясняется принятыми допущениями при теоретическом анализе.

Литература:

1.      Кублановский Я. С., Тиристорные устройства., М.: Энергия., 1981 г.

2.      Кадыров Т. М., Узаков У. З., Касымова Д. Н., «Анализ электрических цепей методом численного решения уравнений состояния», Журнал: Вестник ТашГТУ, № 2, Ташкент, 2005 г., 56–60 с.

3.      Кадыров Т. М., Усманов Э. Г., Абдураимов Э. Х., «Анализ нелинейной динамической цепи с диодным элементом», Журнал: Вестник ТашГТУ, Ташкент, 2006 г., № 3. С 50–53.

4.      Усманов Э. Г., Абдураимов Э. Х., Каримов Р. Ч., «Нелинейная динамическая цепь с тиристором», Журнал: «Проблемы информатики и энергетики», Ташкент, 2006 г, № 2–3, стр. 37–41.