Примерно через сто лет после открытия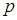 
-адических чисел они в основном рассматривались в качестве объектов чистой математики. Начиная с 1980-х годов различные модели, описанные на языке 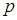-адического анализа, были активно исследованы и до сих пор исследуются. Многочисленные применения 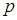-адических чисел к теоретической физике были рассмотрены в работах [1], [2]. А также исследование 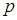-адических динамических систем имеет применения в диофантовой геометрии, в квантовой механике, в биологических и физических системах и во многих других направлениях науки(см. например [1], [3], [4]).
Пусть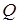 
— поле рациональных чисел. 
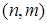-наибольший общий делитель натуральных чисел 
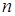и 
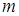. Каждое рациональное число 
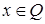можно представить в виде
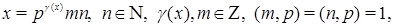
где 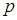-фиксированное простое число. 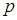-адическая норма 
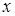имеет вид
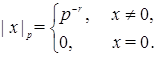
Она имеет следующие свойства:
1) 
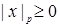и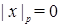 
тогда и только тогда, когда 
,
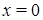2) 
,
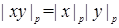3) 
,
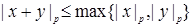a. Если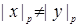 
, то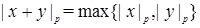 
,
b. Если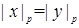 
, то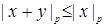 
.
Пополнение 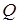по отношению к 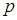-адической норме определяет 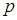-адическое поле, которое обозначается через 
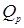. Хорошо известная теорема Островского утверждает, что нормы 
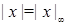и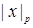 
исчерпывают все неэквивалентные нормы на 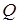(см. [5]). Любое 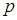-адическое число 
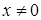может быть однозначно представлено в каноническом виде:
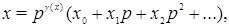
где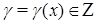 
и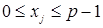 
, 
, 
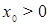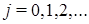(см. [5]).
Заметим, что в этом случае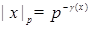 
.
Пополнение алгебраического замыкания 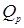обозначается через 
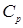и называется множеством комплексных 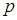-адических чисел. Для любого 
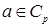и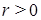 
обозначим
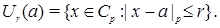
Функция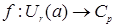 
называется аналитической, если она может быть представлена в виде
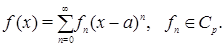
Напомним некоторые определения из теории динамических систем (см. [6]). Если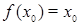 
, то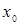 
называется неподвижной точкой.
Пусть 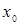является неподвижной точкой аналитической функции 
.
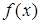Точка 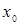называется притягивающей, если 
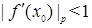, независимой, если 
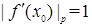, и отталкивающей, если 
.
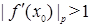Пусть дана функция следующего вида
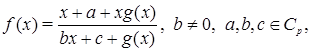
определенная на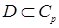 
и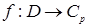 
. Здесь 
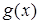произвольная функция и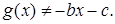 
Решая уравнение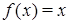 
находим неподвижные точки следующего вида
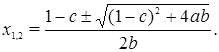(1)
Допустим функция 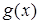на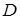 
имеет производную. Тогда
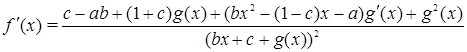
и с учетом (1) мы получим
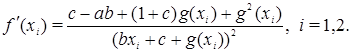(2)
Далее введем следующие обозначения:
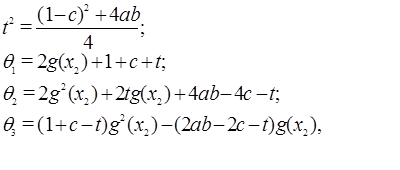(3)
где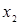 
неподвижная точкa.
Определим функции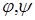 
следуюшим образом
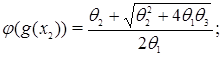
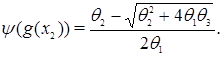
Теорема. Пусть для неподвижных точек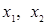 
имеет место 
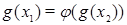или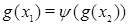 
. Тогда
1. Если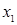 
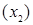притягивающая точка, то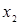 
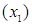отталкывающая;
2. 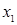и 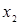одновременно будут независимыми.
Доказательство. Для доказательства теоремы при услови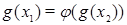и или 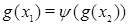достаточно доказать (см. [7]) следующее
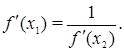(4)
Из условия теоремы будем иметь
.
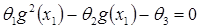И обозначений (3) мы получим
.
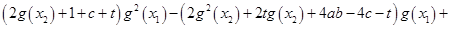
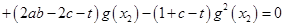Тогда
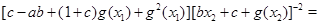
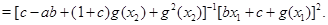
Отсюда, используя равенство (2), получим требуемое равенство (4). Теорема доказана.
Литература:
1. A.Yu.Khrennikov, Non-Archimedean analysis: quantum paradoxes, dynamical systems and biological models, Kluwer, Netherlands, 1997.
2. V. S. Vladimirov, I. V. Volovich and E. I. Zelenov, 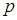-adic Analysis and Mathematical Physics, World Scientific, Singapour, 1994.
3. G.Call and J.Silverman, Canonical height on varieties with morphisms, Compositio Math. 89(1993), 163–205.
4. E.Thiran, D.Verstegen and J.Weters, 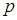-adic dynamics, J.Stat. Phys. 54(3/4)(1989), 893–913.
5. Коблиц Н., 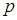-адические числа, 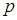-адический анализ и дзета-функции. — М.:Мир, 1982, 192 с.
6. H.-O.Peitgen, H.Jungers and D.Saupe, Chaos Fractals, Springer, Heidelberg-New York, 1992.
7. F. M. Mukhamedov, U. A. Rozikov, On rational 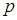-adic dynamical systems. Methods of Func. Anal. and Topology. 2004, V.10, No.2, p. 21–31.
