Введение
В последние десятилетия, в связи с развитием наукоемких технологий, существенно расширился круг задач, связанных со свободноконвективными течениями. Примерами прикладных научных отраслей, в которых интенсивно развиваются и используются результаты исследований естественной конвекции, являются кристаллофизика и космические технологии. Возросшая сложность математических моделей и экспериментальных установок позволяют ставить и решать новые задачи в этих областях.
Хорошо известное приближение Обербека-Буссинеска уравнений Навье-Стокса традиционно широко используется для описания конвективных течений в «земных» условиях. Однако, в случае пониженной гравитации, допущения, при которых оно получено, могут нарушаться, поэтому вопрос о математически корректном и физически оправданном применении модели Обербека-Буссинеска является дискуссионным. Исследованию этой проблемы был посвящен ряд работ В.В. Пухначева и P.S. Perera, R.F. Sekerka (см., например, [1], [2]). В [1] был предложен критерий, ограничивающий область использования уравнений Обербека-Буссинеска, а также представлена модель микроконвекции, позволяющая адекватно описывать течения в микромасштабах или в условиях микрогравитации. Этим критерием является параметр микроконвекции 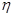 (точный вид см. в п. 2): показано, что аппроксимация Обербека-Буссинеска применима, только если
(точный вид см. в п. 2): показано, что аппроксимация Обербека-Буссинеска применима, только если 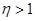 , в противном случае необходимо пользоваться другими моделями. Малость данного параметра обеспечивается либо малыми значениями ширины канала (в этом случае говорят о микромасштабных течениях) и/или гравитационного ускорения (течения в условиях микрогравитации), либо большими значениями кинематической вязкости и/или температуропроводности.
, в противном случае необходимо пользоваться другими моделями. Малость данного параметра обеспечивается либо малыми значениями ширины канала (в этом случае говорят о микромасштабных течениях) и/или гравитационного ускорения (течения в условиях микрогравитации), либо большими значениями кинематической вязкости и/или температуропроводности.
В данной работе исследуется стационарное течение вязкой теплопроводной жидкости в вертикальном канале с неподвижными твердыми стенками, на которых задан поток тепла. Изучается линейная устойчивость течения относительно малых пространственных возмущений в рамках модели микроконвекции (плоские возмущения изучались ранее в работах [3, 4]). Поскольку данная задача возникла в рамках решения проблем кристаллофизики, связанных с выращиванием сверхчистых (без полосчатых неоднородностей) кристаллов полупроводников в невесомости, то значения параметра микроконвекции предполагались 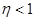 .
.
1. Постановка задачи и определяющие уравнения
Пусть жидкость заполняет плоский вертикальный канал ширины 2a (рис. 1). Границы канала – неподвижные твердые стенки.
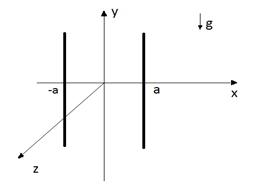
Рис. 1. Схема течения
Для описания движения жидкости воспользуемся моделью микроконвекции [1]:
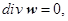
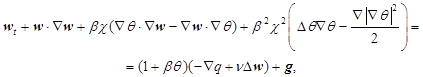 (1.1)
(1.1)
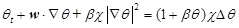 .
.
Здесь 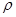 – плотность;
– плотность; 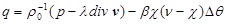 – модифицированное давление;
– модифицированное давление; 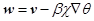 – модифицированный вектор скорости;
– модифицированный вектор скорости; 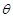 – температура;
– температура; 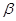 – коэффициент линейного температурного расширения;
– коэффициент линейного температурного расширения; 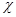 – температуропроводность среды;
– температуропроводность среды; 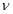 – кинематическая вязкость;
– кинематическая вязкость; 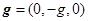 – вектор массовых сил.
– вектор массовых сил.
Так как в дальнейшем рассматриваются только стационарные течения, то для замыкания уравнений зададим на границах условия для скорости и температуры в следующем виде:
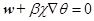 ,
, 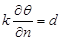 , (1.2)
, (1.2)
где 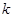 – коэффициент температуропроводности,
– коэффициент температуропроводности, 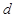 – заданный поток тепла.
– заданный поток тепла.
Известно, что плоские течения в вертикальном слое реализуются, если величина теплового потока не зависит от z, а компонента скорости 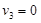 . В [5] показано, что в этом случае решение системы (1.1) представимо в виде
. В [5] показано, что в этом случае решение системы (1.1) представимо в виде 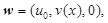
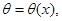
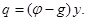 В работе [3] получен точный вид решений с
В работе [3] получен точный вид решений с 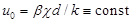 :
:
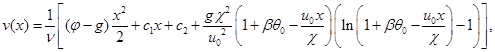 (1.3)
(1.3)
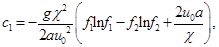
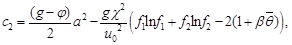
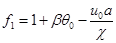 ,
, 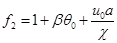 ,
,
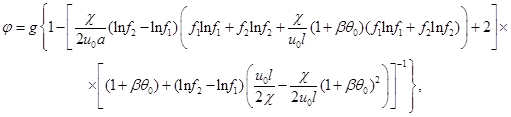 (1.4)
(1.4)
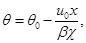
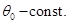 (1.5)
(1.5)
Исследуем устойчивость данного решения в рамках линейной теории.
2. Линеаризованная задача о малых возмущениях
Рассмотрим возмущенное решение исходной задачи 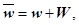
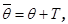
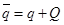 . Подставив новые искомые функции
. Подставив новые искомые функции 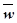 ,
, 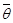 ,
, 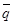 в систему (1.1), (1.2), считая возмущения W, T, Q и их производные малыми, получим линеаризованную задачу:
в систему (1.1), (1.2), считая возмущения W, T, Q и их производные малыми, получим линеаризованную задачу:
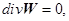
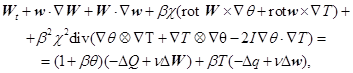
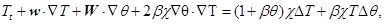 (2.1)
(2.1)
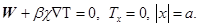
Введем безразмерные переменные следующим образом:
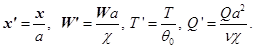
Опуская штрихи, из (2.1) получим:
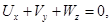
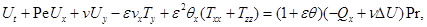 (2.2)
(2.2)
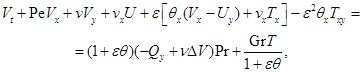
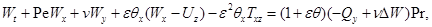
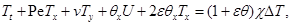
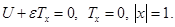
При указанном выборе безразмерных переменных задача (2.2) содержит следующие определяющие безразмерные величины: параметры микроконвекции 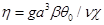 и Буссинеска
и Буссинеска 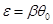 , числа Пекле
, числа Пекле 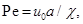 Прандтля
Прандтля 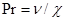 и Грасгофа
и Грасгофа 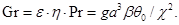
Представим решение краевой задачи (2.2) в виде нормальных волн
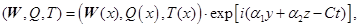 (2.3)
(2.3)
где 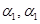 – волновые числа вдоль осей y и z соответственно; С – комплексный декремент, определяющий поведение возмущений со временем. В этом случае возмущение представляет собой волну, распространяющуюся под углом
– волновые числа вдоль осей y и z соответственно; С – комплексный декремент, определяющий поведение возмущений со временем. В этом случае возмущение представляет собой волну, распространяющуюся под углом 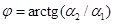 в положительном направлении оси
в положительном направлении оси 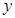 . Подставляя (2.3) в (2.2), получим спектральную задачу:
. Подставляя (2.3) в (2.2), получим спектральную задачу:
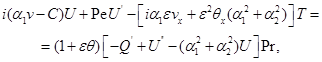
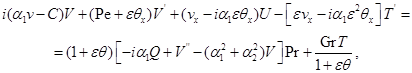
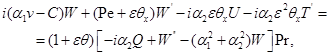 (2.4)
(2.4)
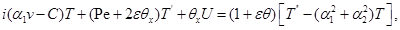
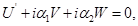
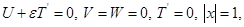
в которой искомые декременты играют роль собственных чисел, а соответствующие им собственные функции, зависящие от 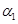 ,
, 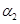 ,
, 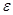 ,
, 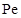 ,
, 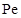 ,
, 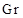 , описывают амплитуды возмущений.
, описывают амплитуды возмущений.
Умножим второе и третье уравнения в (2.4) на 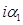 и
и 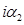 соответственно, и, складывая, получим
соответственно, и, складывая, получим
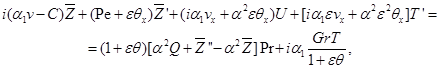
где
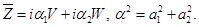
Делая в (2.4) замену
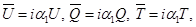
получим плоскую задачу:
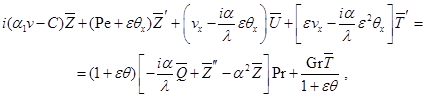
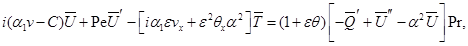
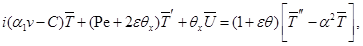 (2.5)
(2.5)
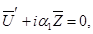
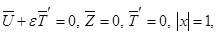
где 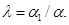
Заметим, что обе задачи позволяют найти декременты возмущений, которые являются собственными числами для задач (2.4) и (2.5), однако только решение системы (2.4) дает искомые амплитуды возмущений.
3. Численное решение задачи на собственные значения
Для решения спектральной задачи (2.4) использовался метод ортогонализации [6]. Для этого (2.4) приводится к системе обыкновенных дифференциальных уравнений вида 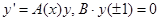 , где
, где 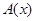 – матрица системы,
– матрица системы, 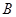 – матрица граничных условий. Так как на каждой границе задано 3 условия, то решение ищется в виде
– матрица граничных условий. Так как на каждой границе задано 3 условия, то решение ищется в виде 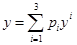 . В качестве начальных данных выбирается полная система векторов, удовлетворяющих условию на левой границе. Затем система интегрируется с помощью метода Рунге-Кутта-Мерсена пятого порядка с автоматическим выбором шага с ортогонализацией в промежуточных точках. Граничное условие на правом конце даст значения искомых коэффициентов
. В качестве начальных данных выбирается полная система векторов, удовлетворяющих условию на левой границе. Затем система интегрируется с помощью метода Рунге-Кутта-Мерсена пятого порядка с автоматическим выбором шага с ортогонализацией в промежуточных точках. Граничное условие на правом конце даст значения искомых коэффициентов 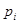 . Для построения нетривиальных решений потребуем равенство нулю определителя
. Для построения нетривиальных решений потребуем равенство нулю определителя 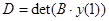 . При фиксированных значениях волновых чисел и безразмерных параметров задача сводится к решению нелинейного уравнения
. При фиксированных значениях волновых чисел и безразмерных параметров задача сводится к решению нелинейного уравнения 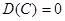 , корнями которого будут собственные числа спектральной задачи. Решение полученного уравнения ищется с помощью метода секущих. Все необходимые, описанные выше, численные процедуры были реализованы в среде MATLAB.
, корнями которого будут собственные числа спектральной задачи. Решение полученного уравнения ищется с помощью метода секущих. Все необходимые, описанные выше, численные процедуры были реализованы в среде MATLAB.
Анализ устойчивости проводился для модельной среды 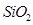 (диоксид кремния), физические параметры которой указаны в таблице 1. В таблице 2 приведены значения ширины канала, гравитационного ускорения и тепловых потоков, которые использовались в расчетах. Данные величины выбирались исходя из выполнения условия микроконвекции и обеспечения такого перепада температур в канале, при котором можно полагать постоянство кинематической вязкости.
(диоксид кремния), физические параметры которой указаны в таблице 1. В таблице 2 приведены значения ширины канала, гравитационного ускорения и тепловых потоков, которые использовались в расчетах. Данные величины выбирались исходя из выполнения условия микроконвекции и обеспечения такого перепада температур в канале, при котором можно полагать постоянство кинематической вязкости.
Таблица 1
Физические параметры среды для 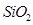
|
Коэффициент температурного расширения β, 1/К |
0.75e-5 |
|
Кинематическая вязкость ν, |
2.65e-3 |
|
Температуропроводность χ, |
0.49 |
|
Теплопроводность k, |
2.16e-1 |
Таблица 2
Параметры задачи
|
Ширина канала 2a, см |
0.2 |
|
Поток тепла d, |
5, 10, 20, 50, 100, 200 |
|
Гравитационное ускорение g, |
981e-6, 981e-3 |
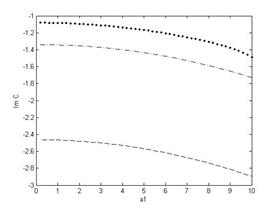
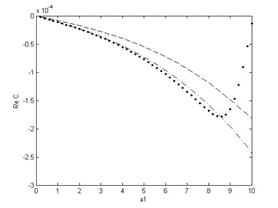
Расчеты, проведенные при волновых числах в диапазоне 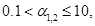 показывают, что мнимые части декрементов отрицательны при любых волновых числах из указанного диапазона, что говорит об устойчивости течения при рассматриваемых значениях физических параметров. При этом вещественные части найденных декрементов отличны от нуля (рис. 2), что говорит о существовании затухающих (в силу знака мнимой части) колебательных режимов.
показывают, что мнимые части декрементов отрицательны при любых волновых числах из указанного диапазона, что говорит об устойчивости течения при рассматриваемых значениях физических параметров. При этом вещественные части найденных декрементов отличны от нуля (рис. 2), что говорит о существовании затухающих (в силу знака мнимой части) колебательных режимов.
Анализ собственных функций показывает, что возмущения представляют собой конвективные ячейки, форма которых зависит от параметров задачи, а пространственные размеры определяются волновыми числами. При этом взаимодействие тепловых и гидродинамических возмущений может приводить к формированию различных конвективных режимов.
|
a)
|
б)
|
|
Рис. 2. Мнимые а) и вещественные б) части декрементов в зависимости от волнового числа |
|
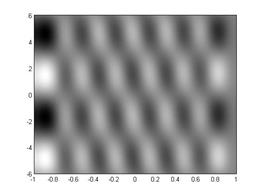
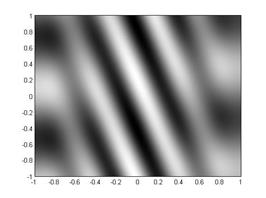
Тепловые возмущения могут иметь форму тепловых валов (рис. 3 а)), «тепловых пятен» (рис. 3 б)) или гидротепловых валов, которые формируются на границе встречных потоков (рис. 3 в), 3 г)). При этом конфигурация валов зависит от длины волны возмущения. Наиболее разнообразное семейство характеристических возмущений температуры наблюдается в случае коротковолновых возмущений.
|
а)
|
б)
|
|
в)
|
г)
|
|
Рис. 3. Температурные возмущения при разных волновых числах а) – |
|
Гидродинамические возмущения могут приводить к формированию в слое мелкомасштабных ячеек. При этом гидротепловые валы (рис. 3 г), 4 а)) образуются в результате совместного влияния тепловых и гидродинамических возмущений. С ростом теплового потока на стенках (фактически это влияет на значение числа Пекле и величину поперечной скорости) не происходит существенного влияния на начальное распределение возмущений полей скорости (рис. 4), что позволяет сделать вывод о стабилизирующем влиянии поперечного продува.
|
а) |
|
|
б) |
|
|
в) |
|
Рис. 4. Влияние теплового потока на начальные возмущения скорости.
а) – d = 50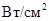 ; б) – d = 200
; б) – d = 200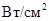 ; в) – d = 500
; в) – d = 500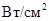
Следует отметить, что при увеличении потока тепла, которое, в силу вида решения, влечёт за собой рост горизонтальной компоненты скорости, не выделено существенных различий в поведении возмущений. Таким образом, можно сделать вывод о том, что тепловой механизм не будет наиболее опасным, более того, поперечный продув оказывает стабилизирующее влияние и приводит к формированию конвективных ячеек по всей ширине канала.
Заключение
В работе изучена устойчивость одного точного решения, описывающего течение жидкости в плоском вертикальном канале в рамках модели микроконвекции. Представлены уравнения, описывающие поведение малых возмущений. Для модельной среды «диоксид кремния» доказана устойчивость при физически разумных значениях параметров задачи, показана возможность существования затухающих колебательных режимов. Рассмотрено влияние параметров на форму начальных возмущений и на основе численных расчётов установлено, что в канале могут формироваться конвективные структуры типа "тепловых пятен", гидротепловых валов и мелкомасштабных ячеек.
Литература:
1. Пухначёв В.В. Модель конвективного течения при пониженной гравитации. Моделирование в механике, 1992. – Т. 6.
2. Perera P.S., Sekerka R.F. Nonsolenoidal flow in a liquid diffusion couple // Phys. Fluids, 1997. – V. 9(2). – P. 376–391.
3. Андреев В.К., Бекежанова В.Б. Об устойчивости стационарного течения в вертикальном слое в модели микроконвекции // Изв. РАН, МЖГ, 2004. – № 2.
4. Бекежанова В.Б. Об устойчивости стационарного неизотермического течения в вертикальном слое с проницаемыми границами в модели микроконвекции // Изв. РАН, МЖГ, 2006. – № 3.
5. Андреев В.К., Капцов О.В., Пухначёв В.В., Родионов А.А. Применение теоретико-групповых методов в гидродинамике. – Новосибирск: Наука, 1994.
6. Годунов С.К. О численном решении краевых задач для систем линейных ОДУ // Успехи мат. наук, 1961. – Т. 6, вып. 3.







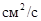
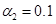 , «-.» –
, «-.» – 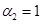 , «--» –
, «--» – 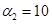
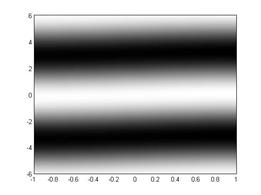
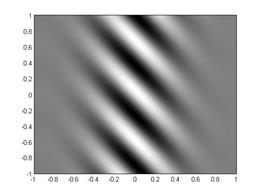
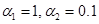 ; б) –
; б) – 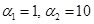 ; в) –
; в) – 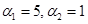 ; г) –
; г) –