В настоящее время наблюдается повышенный интерес к исследованию влияния осевых зазоров в турбинных ступенях, в частности, на величины нестационарных нагрузок. Обычно предполагается, что увеличение осевых зазоров полезно как точки зрения уменьшения нестационарных нагрузок, так и КПД ступени [1–7]. Но уже в работах [1, 2] было указано на немонотонное изменение нагрузок и КПД ступени при изменении осевого зазора.
Первоначальные работы в 60-х по влиянию осевого зазора на переменные аэродинамические силы были выполнены экспериментально в МЭИ [5] и ЛПИ [1–4]. Для исследования нестационарного течения в ступени турбомашине в ЛПИ были созданы экспериментальные турбины, опытами на одной из которых (обращенная радиальная турбина ЭТН-ЛПИ [1, 4]) были оценены уровни нестационарных нагрузок, которые могли приводить к усталостными поломам рабочих лопаток.
Ozaki S. и др. (2013) [7] исследовали влияние осевого зазора на пульсации давления на 1,5 ступени турбины. Авторы заключили, что локальный минимум амплитуды возбуждающей силы находится в области маленького зазора из-за большой интерференции направляющего аппарата и рабочего колеса. Эффект потенциальной интерференции был найден в фазе вблизи входной кромки рабочей лопатки. Возбуждающая сила интенсивно изменена в осевом зазоре потому, что маленький зазор сильно влияет на амплитуду пульсации давления на поверхности лопатки. Влияние осевого зазора на нестационарное давление было сильнее, чем при изменении различных других условиях эксперимента.
В настоящее время в связи с развитием вычисленной гидродинамики и в частности с появлением коммерческих пакетов типа ANYS CFX появилась возможность исследования процессов нестационарных течений в турбомашинах. В работе представлены результаты численного моделирования влияния изменения межвенцовых осевых зазоров на величину переменных аэродинамических сил (ПАС), вызывающих колебания рабочих лопаток. Результаты численного исследования были сопоставлены с экспериментальными данными, полученными при исследовании обращенной радиальной модели в СПбПУ [4].
1. Постановка задачи и методы расчета
Расчетные модели представлены на рис. 1 с различными осевыми зазорами Δz1=4÷35мм. Основные геометрические размеры представлены в табл.1.
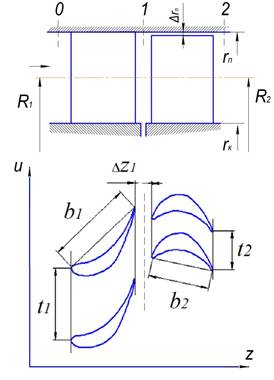
Рис. 1. Схема геометрической модели ступени осевой турбин: 1 — лопатки статора; 2 — лопатки ротора
Таблица 1
Геометрические параметры осевой турбины
|
390,12 |
|
|
Длина направляющей и рабочей лопатки, l1= l2 мм |
60 |
|
Хорда, b1 мм |
59 |
|
Шаг, t1 мм |
47,9 |
|
Относительный шаг, |
0,8 |
|
Число сопловых лопаток, m1 |
51 |
|
Хорда, b2 мм |
41 |
|
Шаг, t2 мм |
25,4 |
|
Относительный шаг |
0,618 |
|
Число рабочих лопаток, m2 |
96 |
|
Осевой зазор ступени, ∆z1 мм |
4÷35 |
Основной метод исследования — численное моделирование нестационарных процессов обтекания в турбомашинах, представленное в пакете ANSYS CFX. Предварительные расчеты изменения нестационарных сил во времени выполняются методом Frozen Rotor. Для расчетов нестационарных режимов используется метод Transient Rotor-Stator. Численное моделирование при использовании коммерческого гидродинамического пакета Ansys CFX 14.5 с применением кластера в СПбПУ. Схема расчетной модели течений представлена на рис.2.
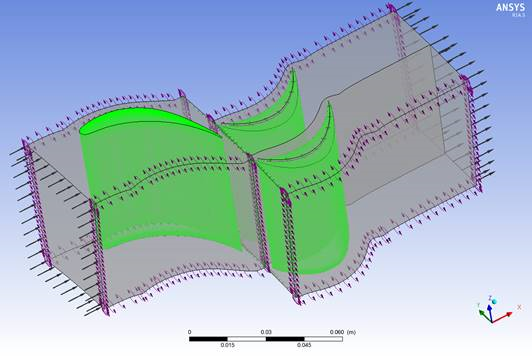
Рис. 2. Расчетная модель ступени осевой турбины
Значение относительного размаха аэродинамической силы определяется по соотношению:
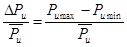, (1)
где Pu — проекции тангенциальной нестационарной аэродинамической силы на направление u;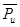 
— осредненная по времени нестационарная аэродинамическая сила; Рumax и Pumin — максимальные и минимальные значения.
2. Результаты численного исследования
Нестационарные силы Pu(τ), действующие на рабочую лопатку (при осевом зазоре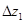 
= 4 мм), получены из численных расчетов и представлены на рис. 3.
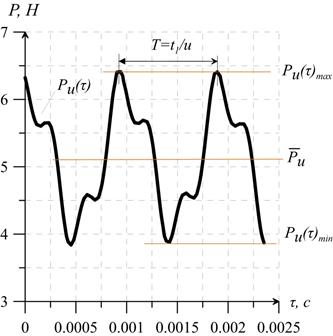
Рис. 3. Нестационарная сила, действующая на рабочую лопатку при осевом зазоре 4 мм
Результат расчетов показан, что изменение размаха аэродинамических сил находится в пределах 10÷30 % от осредненных по периоду значений, что соответствует экспериментальным данным [1]. Этот уровень нестационарных нагрузок может быть опасным при околорезонансных режимах и низких уровнях демпфирования.
В работе [3] показано в том, что в качестве безразмерной характеристики осевого зазора целесообразно использовать величину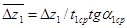 
, где Δz1- осевой зазор, t1cp- шаг решетки, α1cp — угол выхода потока из направляющей лопатки на среднем сечении. Величина 
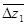характеризует условия суперпозиции потенциальной и вязкой неравномерностей потока за направляющим аппаратом. Введем понятие относительной аэродинамической силы в зависимости от 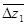по формуле:
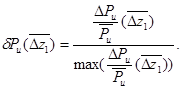(2)
Зависимость относительной аэродинамической силы от безразмерной координаты 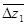представлена на рис. 2а. Сравнение результата с экспериментом представлено на рис.2б.
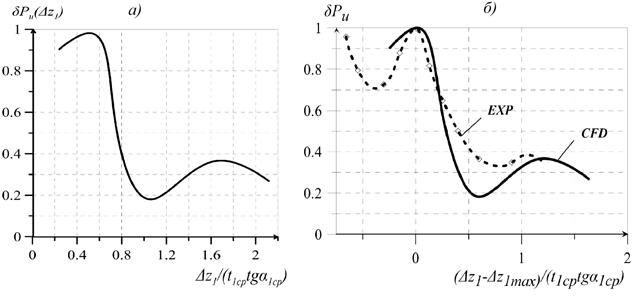Рис. 4. Зависимость относительной аэродинамической силы: а) от безразмерной координаты Δz1/(t1cptgα1cp); б) от (Δz1- Δz1maх)/(t1cptgα1cp) при сравнении эксперимента (EXP- [3]) и численного моделирования (CFD).
Заключение
Основные результаты выполненных численных моделирований следующие:
1) Уровень размахов ПАС в диапазоне относительных зазоров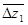 
= 0,2 ÷ 2,2 находится в пределах в диапазоне от 
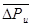=10 % до 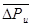=30 %;
2) Общая тенденция изменения ПАС при увеличении зазоров характеризуется уменьшением нестационарных сил, но это изменение не монотонно. Имеется два максимума ПАС в области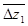 
= 0,6 и 1,6;
3) Область зазоров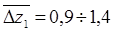 
, в котором возбуждение минимально, может быть рекомендована для практического использования при проектировании турбинных ступеней близкой конфигурации;
4) Результаты численного моделирования согласуются с экспериментом при сопоставлении относительного максимального осевого зазора (рис. 2б).
Литература:
1. Ласкин А. С., Кириллов И. И. Исследование переменных аэродинамических сил в турбинной решетке, обтекаемой нестационарным потоком // Энергомашиностроение., № 12, 1966— с. 17–19.
2. Ласкин А. С. Выбор оптимального осевого зазора, обеспечивающено минимум аэродинамического возбуждения колебаний рабочих лопаток газовой турбины //, № 2, 1987.
3. Ласкин А. С. Метод определения оптимального осевого зазора в турбинной ступени // Проб. машиностроения, 1980. — c. 73–77.
4. Афанасьева Н. Н., Ласкин А. С., Лапшин К. Л., Черников В. А. и др. Аэродинамические характеристики ступеней тепловых турбин, под ред. Черников В. А. — Ленинград: Машиностроение, Ленингр. отд-ние, 1980. — 263 c.
5. Самойлович Г. С. Возбуждение колебаний лопаток турбомаши, Москва, 1975.
6. Funazaki K., Yamada K., Kikuchi M., Sato H. Detailed Studies on Aerodynamic Performance and Unsteady Flow Behaviors of a Single Turbine Stage with Variable Rotor-Stator Axial Gap // International Journal of Gas Turbine, Propulsion and Power Systems (Japan)., № 2 (1), 2008. — pp. 30–37.
7. Yutaka Yamashita, Kiyoshi Segawa, Shuichi Ozaki. Experimental and numerical investigations of the influences of axial gap between blade rows on pressure fluctuation // ISUAAAT 13 — S9–4., Tokyo, Japan, 2013.
