The problem of developing tested estimation methods for unsteady loads, which induce vibration of blade systems and in some cases cause their fatigue breaks, is one of the most important in modern turbine engineering, both in Russia and in the world [1–3].
The article presents the results of a numerical study of levels and nature of unsteady loads on rotor blade in axial turbine stage with various regime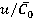 
. The numerical results were compared with experimental data obtained during the study of radial model at St. Petersburg Polytechnic University [4, 5].
Statement of the objectives and estimation methods
Within the frameworks of this research the following objectives were stated:
- assessment of levels and features of unsteady loads on rotor blades in a simulation of a turbine blade row under alteration of its modes of operation, characterized by the correlation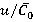 
;
- comparison of the obtained results with experimental data.
Blading section of the model is shown in figure 1, and main dimensions are shown in table 1. Rotor angular velocity was changed from 900 to 1800 rev/min, which changes the correlation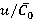 
.
The main analysis method was numerical simulation of unsteady processes in turbo machines performed by ANSYS CFX 14.5 software. Numerical mesh was created using TurboGrid package. All numerical simulation were performed on the Computational Resource Department’s cluster of SPbPU.
Momentary forces and torques Pu(τ), Mz(τ) acting on rotor blade were determined under unsteady simulations (Transient Stator-Rotor) for each point of time τ=t1/50u. Values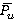 
, 
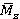were determined by time averaging of values Pu(τ) and Mz(τ).
Variation ranges of force and torque were calculated using the formulas
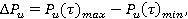(1)
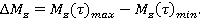(2)
Range of unsteady loads are represented as fractions of time-averaged loads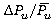
and 
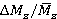. (3)
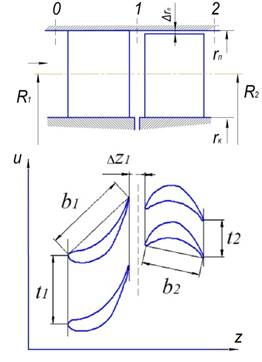
Fig. 1. Geometrical model of axial turbine stage: 1 — stator blades; 2 — rotor blades
Table 1
Geometrical parameters of the axial turbine stage
|
Stator midspan radius, R1 mm |
|
|
Length of stator blade, l1 mm |
60 |
|
Stator blade width, b1 mm |
59 |
|
Stator pitch, t1 mm |
47.9 |
|
Number of nozzle blade, m1 |
51 |
|
Rotor blade width, b2 mm |
41 |
|
Rotor pitch, t2 mm |
25.4 |
|
Number of rotor blades, m2 |
96 |
|
Stator-rotor spacing, ∆z1 mm |
4 |
|
Rotor blade tip clearance, ∆rtip mm |
1 |
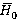is enthalpy variation estimated according to the formula
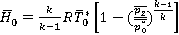. (4)
The numerical results were presented with varying correlation 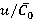, where
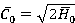≈ const.
Results
Unsteady rotor blade forces Pu(τ) and torques Mz(τ) (at ω = 1300 rev/min) were obtained by numerical simulation and are shown in figure 2. Forces and torques act on rotor blade periodically, with the period of T=9.02 10–4 s. Variation ranges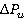 
, 
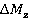were determined by the formulas (1) and (2).
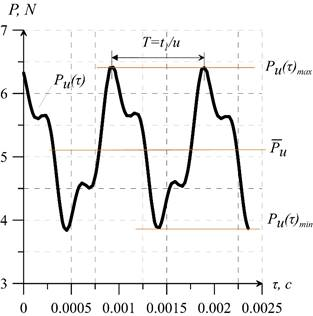
Fig. 2. Unsteady blade force and torque at ω = 1300 rev/min
Correlations of time-averaged loads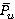 
,
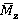, and respective variation ranges , 
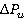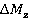from 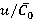are shown in figure 3–4. As rotation speed increases time-averaged values of blade loads (forces and torques) decrease, but range variations of unsteady loads increase.
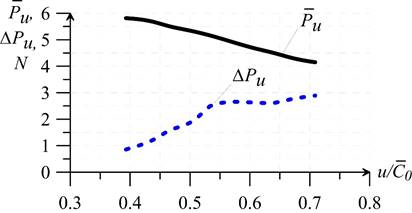
Fig. 3. Correlations of time-averaged force and variation range of force 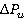from
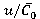(regime 
)
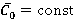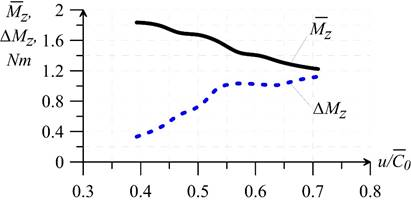
Fig. 4. Correlations of time-averaged torque 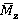and range variation of torque 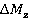from
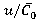(regime )
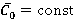In figure 5 alteration of relative unsteady forces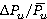 
and torques 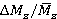on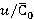 
is presented. Matching of alteration trends is noted. The obtained values of relative range variations of unsteady blade forces and torques match with the data [1–3]. Figure 5 also demonstrates values of dimensionless load per unit 
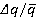in relation to 
(
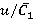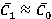), estimated with approximate semi-empirical integral method [4]. General trend of increase of dimensionless load under growth of 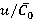were confirmed. Range variation level of unsteady loads under nominal regime
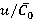=0.55 is 50–60 % of time average values. Increase of dimensionless loads are governed by low axial clearance Δz1 = 4 mm [6]. Range variations of dimensionless loads (forces 
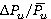and torques 
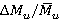) within the range 
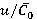of 0.4 to 0.75 increase from 20 % to 90 % of time-averaged values.
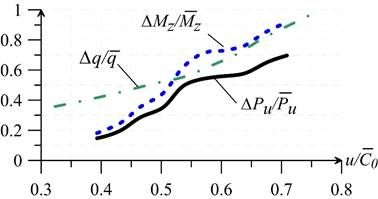
Fig. 5. Dependences of dimensionless forces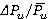 
, torques 
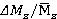and dimensionless per unit loads Δq/
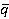(experimental [4]) on 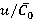(regime )
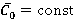Dependence of relative aerodynamic force on dimensionless coordinate Δz1/(t1avtgα1av) is shown in figure 6 [6]. This figure explains the high level of unsteady loads under low axial clearance Δz1 = 4 mm or Δz1/(t1avtgα1av) = 0.2 (point A).
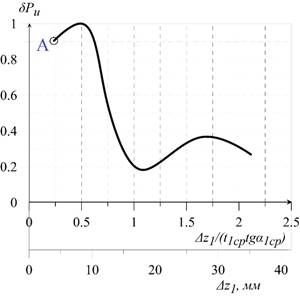
Fig. 6. Dependence of relative aerodynamic force on Δz1 and dimensionless coordinate Δz1/(t1avtgα1av) [6]
Conclusions
1) As rotation speed increases time-averaged values of loads (forces and torques) on rotor blade decrease, however range variations of unsteady loads increase.
2) Range variation level of unsteady loads under nominal regime 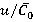= 0.55 and axial clearance Δz1 = 4 mm (Δz1/b1 = 0.067) is 50–60 % of time-averaged loads on rotor blade.
3) Range variations of dimensionless loads (forces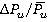 
andtorques 
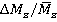) within the range 
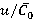(regime 
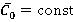) of 0.4 to 0.75 increase from 20 % to 90 % of time average loads on rotor blade.
References:
1. Denos R., Busby J. A. Investigation of the Unsteady Rotor Aerodynamics in a Transonic Turbine Stage // Journal of Turbomachinery. — № 123, — Issue 1. — January 2001. — pp. 81–89.
2. Yamada K., Funazaki K., Kikuchi M., Sato H. Influences of Axial Gap Between Blade Rows on Secondary Flows and Aerodynamic Performance in a Turbine Stage // Proceedings of ASME Turbo Expo 2009: Power for Land, Sea and Air, GT2009–59855. — Orlando, FL, USA, 2009.
3. Dring R. P., Joslyn H. O., Hardin L. W., and Wagner J. H. Turbine rotor-stator interaction // ASME Journal of Power Engineering for Power. — № 104. — 1982. — pp. 729–742.
4. Laskin A. S., Issledovaniye aerodinamicheskogo vozbuzhdeniya kolebaniy lopatochnogo apparata i poter energii pri nestatsionarnykh protsessakh v turbinakh [Research of aerodynamic excitation loads and energy losses in the unsteady processes in turbines] LPI, Leningrad, Abstract, 1980 (in Russian).
5. Afanasyev N. N., Laskin A. S., Lapshin K. L., Chernikov V. A. et al. Aerodinamicheskiye kharakteristiki stupeney teplovykh turbin [Aerodynamic characteristics of thermal turbines stages] ed. Chernikov V. A. — Leningrad, 1980. — 26p (in Russian).
6. Nguyen K. K., Laskin A. S., Chislennoye modelirovaniye vliyaniya osevogo zazora na nestatsionarnyye sily v turbinnoy stupeni [Numerical investigation of the influences of axial spacing between blade rows in an axial turbine on aerodynamic force] // Nauchno-tekhnicheskie vedomosti SPbPU — St. Petersburg State Polytechnic University Journal. — № 2 (195). pp. 65–69. — 2014 (in Russian).
