In the given article the possibilities of the elements’ of count theories and MathCAD in nodal equations’ solving of electrical circuit were analyzed.
Ключевые слова: электрические схемы, граф, MathCAD, матрица, СЛАУ.
Схемы замещения современных сложных электрических систем содержат десятки и даже сотни узлов и ветвей. Количество уравнений состояния для таких систем соответственно настолько велико, что для их решения необходимо использовать цифровые электронные вычислительные машины.
Более того, составление уравнений состояния для сложных схем является весьма трудоемкой процедурой, и решение данной задачи также целесообразно возложить на компьютер. Для этого требуется иметь формализованный подход к составлению уравнений, который был бы одинаков для схем любой сложности и конфигурации. Такой подход может быть разработан на основе аналитического представления конфигурации схемы замещения с помощью элементов теории графов и алгебры матриц.
Конфигурацию схемы замещения электрической системы можно отобразить в виде графа. Граф представляет собой множество вершин (узлов) и ребер (ветвей), соединяющих некоторые (а может быть и все) пары вершин. Если ребра графа имеют фиксированные направления, то этот граф называется направленным. Каждое ребро направленного графа имеет начальную и конечную вершину: его направление принимается от первой вершины ко второй. Схема замещения электрической системы обычно является связанным графом. Она состоит из ветвей (ребер), соединенных в узлы (вершины). Все величины, характеризующие состояние ветвей (токи, ЭДС, падения напряжения), имеют определенное направление (без чего не может быть рассчитан режим данной схемы). В связи с этим целесообразно каждой ветви схемы придать определенное, с произвольно выбранным, направлением. Таким образом, схема замещения системы обычно является связанным направленным графом, ребрами которого служат ветви, а вершинами узлы. При изображении схем в виде графов нет надобности в специальных обозначениях сопротивлений и ЭДС. Ветви графически изображаются (прямой или кривой) с указанием их направлений. Таким образом, направление ветви от начального узла к конечному узлу одновременно является положительным направлением и для всех участвующих величин — ЭДС, тока и падения напряжения. Любая из этих величин может получиться положительной или отрицательной по отношению к принятому направлению.
В данном статье анализируем вожмозности элементов теории графа и МathCAD при решении узловых уравнений электрических схем.
Для иллюстрации вышесказанного рассмотрим следующую электрическую схему:
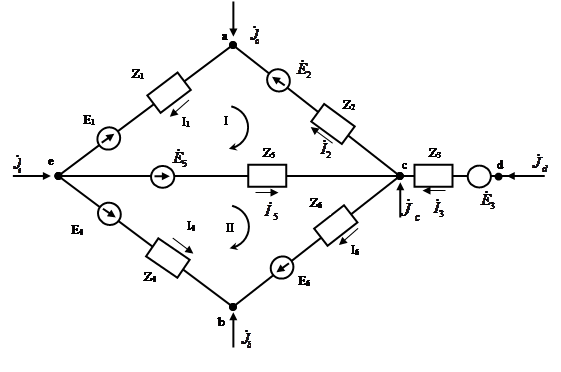
Рис. 1
|
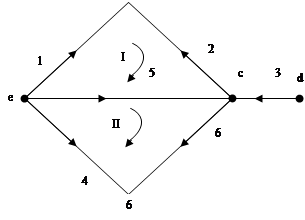
Рис.2
Для направленного графа могут быть определены:
1) матрица соединений ветвей в узлах (первая матрица инциденций)
2) матрица соединений ветвей в независимые контуры (вторая матрица инциденций), служащие для обобщенного аналитического представления графа.
Матрица соединений ветвей в узлах-это прямоугольная матрица, число строк которой равно числу вершин графа n, а число столбцов-числу ребер m. Она обозначается следующим образом:
.
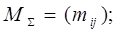
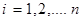
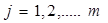При этом номера строк i-соответствуют номерам вершин, а номера столбцов j-номерам ребер. Элементы матрицы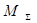 
могут принимать одно из трех значений:
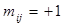, если узел 
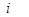— является начальной вершиной ветви 
;
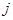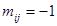, если узел 
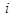— является конечной вершиной ветви ;
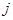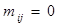, если узел 
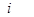— не является вершиной ветви ;
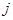Для направленного графа, показанного рис. 2, матрица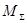 
имет вид:
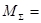
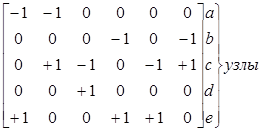
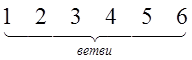
Выбрав узел е в качестве балансирующего, получим матрицу M из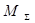 
путем исключения последней строки:
M=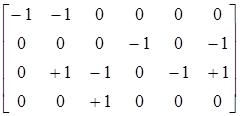
Матрица соединений ветвей в независимые контуры это прямоугольная матрица, число строк которой равно числу независимих контуров графа к, а число столбцов числу ветвей m. Она обозначается следующим образом:
, 
, 
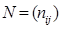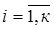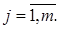
При этом номера строк i соответствуют номерам независимы контуров, а номера столбцов j номерам ветвей. Элементы матрица N определяются следующим образом:
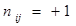, если ветвь j входит в контур i и их направления совпадают;
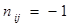, если ветвь j входит в контур i и их направления противоположны;
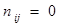, если ветвь j не входит в контур i.
Для направленного графа, показанного на рис.2, матрица N имеет вид:
N=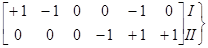
независимые контуры
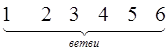
Матрица M и N дают возможность записать уравнения состояния электрической цепи в матричной форме. Система взаимно независимых уравнений первого закона Кирхгофа может быть представлена в виде
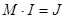(1)
где 
, 
, 
, 
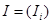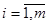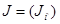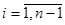— столбцы токов в ветвях и задающих токов в узлах соответственно.
Аналогично система взаимно независимых уравнений второго закона Кирхгофа может быт записано в виде
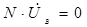(2)
где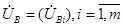 
- столбец падений напряжений на ветвях схемы.
Система, состоящая из (n-1) уравнений, связывающих напряжения узлов относительно балансирующего с задающими токами в узлах и ЭДС в ветвях, называется системой узловых уравнений. Оно широко применяется в практике расчетов установившихся режимов сложных электрических систем. Система узловых уравнений имеет следующий вид [2]:
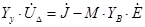(3)
где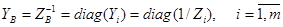 
—матрица проводимостей ветвей,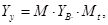 
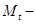транспонированная матрица М. При отсутствии ЭДС в ветвях, что характерно для большинства схем замещения реальных электрических систем, матричное узловое уравнение (3) имеет наиболее простой вид. Тогда при 
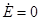получаем
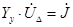(4)
видно, что формирование узловых уравнений вида (4) сводится к определению матрицы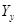 
.
После определения матрицы 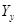задача сводится к решению систем алгебраических уравнений относительно к 
.
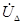Методы решения СЛАУ можно разделить на две большие группы: прямые и итерационные.
В последние время появились многие пакетные программы, с помощью которых появилась возможность решения математических задач (в том числе и других задач науки, описывающее такими же математическими моделями) без составления компьютерных программ [1,2]. В учебном процессе (иногда и в научных учреждениях) с помощью использования таких систем как MathCAD, Maple, Matlab, Mathematika и. т.д занятия становятся интереснее, осмысление содержания занятия более быстрое и глубокое а также на укрепление излагаемых понятий и на решение задач остаётся достаточно много времени. Из выше указанных систем, MathCAD — более проще чем остальные и она предназначена для технических вузов, а остальные, можно сказать, для профессиональных математиков. Именно в MathCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.
Приведём алгоритм задачи:
- данная электрическая цепь преобразуется в виде графа;
- определяются матрицы M и N;
- с помощью матрицы M определяются матрица Yy; (при этом определение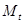 
и операции над матрицами возможно при помощью Маthcad)
- система уравнения решается методом обратной матрица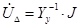 
. (решения СЛАУ — при записи методом обратной матрицы проще, чем в остальных методах и требует меньшее затраты времени)
При исходных данных [2]: (именно эти данные берутся, чтобы сопоставить результаты)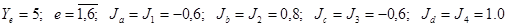 
в окне МathCAD введём следующие команды и получаем результаты:
Полученные результаты совпадают с приведенными результатами [2].
В заключении можно сказать что, при вычислении электрических схем, таким путём, вручную не выполняются какие-то арифметические операции, не требуется применение законов, а только схема преобразуется в виде графа, определяются матрица М (видно, что это не имеет сложности) и с помощью выше указанного алгоритма решается узловое уравнение. Естественно, что при решение любой практической задачи невозможно без арифметических операций, но при этой работе особенно важный фактор является тот фактор, что без арифметических операций получаем результаты. Операции над матрицами и решения СЛАУ возложили на МathCAD.
Литература:
1. Тиллабоев Ё.К, Дадамирзаев М., Абдулхафизов Б. Об одном из методов решения уравнения Навье-Стокса. Молодой учёный. № 6, (86), март 1, 2015 г. с. 7–11.
2. В. А. Веников и др. Математические задачи электроэнергетики. М., Высшая школа, 1987г.
3. Охарзин.В. А. Прикладная математика в системе Mat CAD. СПб, Лань, 2008г. -352с.
