При проведении экспериментов или опытов получаются случайные величины, появление которых предсказать невозможно, и они чаще всего подчиняются нормальному закону распределения (закону Гаусса). Данный закон распределения применяется во многих областях науки, в том числе и при оценки качества изделий, и является моделью для многих реальных процессов. Это объясняется тем, что он является предельным законом, к которому приближаются другие законы распределения и обладает «правилом трех сигм», которое имеет большое практическое применение.
Кривую нормального закона распределения называют нормальной (гауссовой) кривой (рис. 1) и описывают выражением:
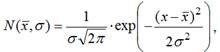(1)
где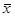 
— среднее значение; 
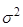— дисперсия, 
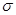— среднеквадратическое отклонение (СКО).
а) б)
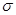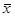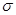Параметрами и определяется положение кривой относительно начал координат и ее форма. В качестве образца принимают кривую распределения с =0 и =1.
К особенностям кривой нормального распределения следует отнести:
1) кривая симметрична относительно среднего арифметического 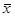, которое равно моде и медиане распределения;
2) кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до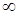 
. Следовательно, чем больше значение х отличается от среднего арифметического 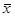распределения, тем реже данное значение встречается в выборке;
3) кривая имеет две точки перегиба, находящиеся на расстоянии ± 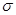от ;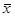
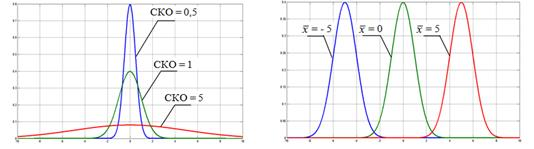
4) при 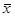=const с возрастанием 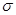кривая становится более пологой, а при уменьшении 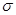- более «островершинной» (рис. 1а). При 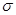= const с изменением 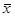кривая не изменяет форму, а сдвигается вправо или влево по оси абсцисс (рис. 1б);
5) в промежутке 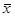± 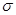находится 68,3 % всех значений признака; 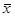± 2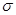 — 95,4 %; 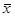± 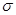— 99,7 %;
6) коэффициент асимметрии As=0 и коэффициент эксцесса Ex=m4/s4 = 3.
а) б)
Рис. 2. Кривая нормального распределения (1) с различными значениями коэффициента асимметрии As (а) и коэффициента эксцесса Ex(б)
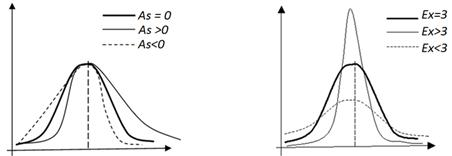
Процесс формирования формы кривой нормального распределения можно проследить при построении контрольных карт, которые используются для контроля качества изделий и анализа технологического процесса. Результаты измерений по каждому образцу отмечают в контрольной карте отдельной точкой, отбирая, например, по 5 образцов через каждый час или через 100 штук обработанных изделий, замеряя их, а результаты, занося в карту. В результате можно получить следующие варианты распределения:
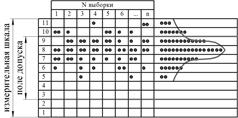
1 вариант. Измеряемые детали не выходят за пределы поля допуска (рис. 3а).
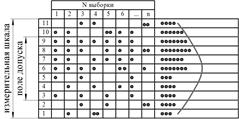
2 вариант. Необходима подналадка, так как распределение вышло за пределы поля допуска (рис. 3б).
3 вариант. Наладкой станка исправить положение невозможно, необходимо искать другие причины такого большого разброса размеров (рис. 3в).
а) б)
в)
Рис. 3. Варианты контрольных карт
На основании визуального анализа контрольных карт (рис. 3) формулируют выводы о дальнейшем управлении технологическим процессом.
Для анализа распределения необходимы числовые значения статистических показателей, позволяющие оценить колебания значений изучаемого признака и взаимосвязь его с другими признаками:
- частотные показатели (частота и относительная частота);
- показатели центра распределения (средняя величина, мода, медиана);
- показатели степени вариации (размах, дисперсия, СКО, коэффициент осцилляции, коэффициент вариации);
- показатели формы распределения (асимметрия и эксцесс).
Кроме этого, стоит отметить, что распределения характеризуются числовыми характеристиками, которые называются моментами случайных величин. Нормальное распределение описывается четырьмя основными моментами: математическое ожидание (МО), дисперсия, коэффициент асимметрии As и коэффициент эксцесса Ех (таблица 1).
Таблица 1
Геометрический смысл основных моментов нормального распределения
|
Обозн. |
Название момента |
Геометрический смысл |
|
m1 |
Математическое ожидание (среднее арифметическое |
Показывает расположение относительно начала координат |
|
m2 |
Дисперсия |
Показывает разброс вокруг среднего |
|
m3 |
Коэффициент асимметрии As |
Характеризует асимметрию распределения |
|
m4 |
Коэффициент эксцесса Ех |
Показывает, насколько выражена вершина распределения |
Для вычисления статистических показателей используют специальные программы, например Statistica, и другие программы — от электронных таблиц MS Excel до математических пакетов (Mathcad, Matlab, Scilab и др.). Количество доступных статистических функций последних, сегодня почти не уступает специальным программам [1].
В статье [1] рассмотрен статистический анализ партии обработанных изделий в MS Excel, на примере измерений детали Втулка Ø8,5Н14 (рис. 4).
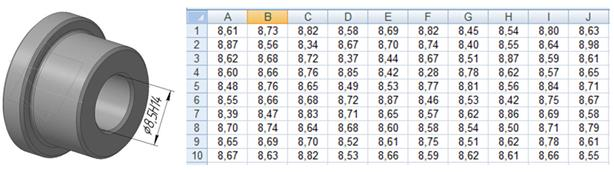
Рис. 4. Втулка Ø8,5Н14 и выборка по внутреннему диаметру втулки [1]
Проведем статистический анализ в математическом пакете Matlab. Вначале запишем программу вычисления основных статистических показателей в М-файле, листинг приведен на рис. 5. Данные загружаются из файла MS Excel — statistica.xls.
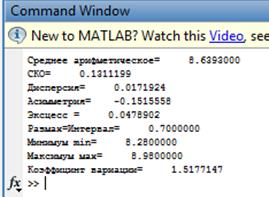
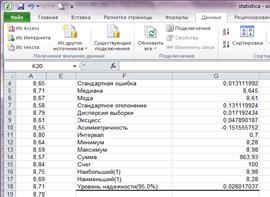
В окне Command Windows получается результат вычисления (рис. 6а), который можно сравнить с результатами, полученными в MS Excel с помощью пакета Анализ данных — Описательная статистика (рис. 6б). Анализ показывает, что значения одних и тех же показателей совпадают, а перечень показателей, предлагаемые MS Excel, не содержит среднего арифметического 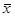и коэффициента вариации.
а) б)
Рис. 6. Результаты расчета показателей при помощи Matlab (а) и MS Excel (б)
В математическом пакете Matlab есть специальные наборы инструментов Toolbox, предназначенные для решения определенного класса задач, например, для решения задач статистики — Toolbox Statistics. Кроме этого есть Simulink — графическая среда имитационного моделирования, позволяющая при помощи блок-диаграмм в виде направленных графов, строить модели систем и вычислений по следующему алгоритму (рис. 7).
Рис. 7. Алгоритм моделирования в Matlab/Simulink
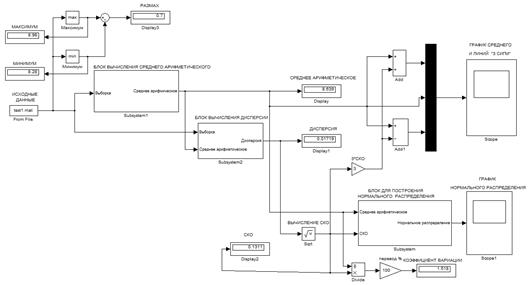
В Библиотеке стандартных блоков Matlab/Simulink не все разделы доступны, поэтому возникает задача создавать свои блоки из доступных блоков с помощью блока Subsystem. В нашем случае, создается три блока Subsystem для вычисления среднего арифметического, дисперсии и для построения нормального распределения (рис. 9).
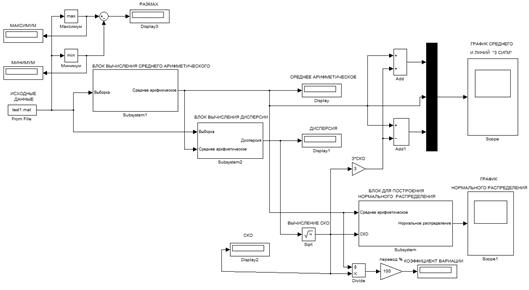
Рис. 8. Схема для вычисления статистических показателей в Matlab/Simulink
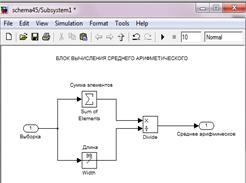
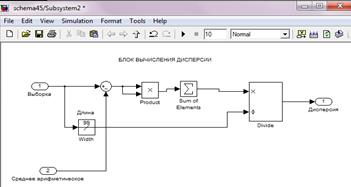
а) б)
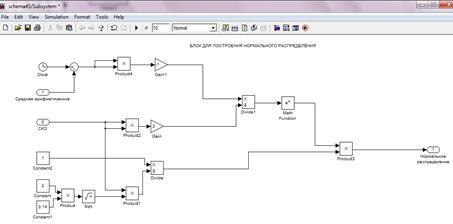
в)
Рис. 9. Схемы блоков для вычисления статистических показателей в Matlab/Simulink
В результате моделирования получаются значения (рис. 10), совпадающие со значениями, полученными при помощи Matlab и MS Excel (рис. 6):
- Минимальное значение 8,28;
- Максимальное значение 8,98;
- Размах 0,7;
- Среднее арифметическое 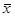=8,639
- Дисперсия 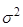=0,01719;
- СКО 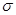=0,1311;
- Коэффициент вариации 1,518 %.
Анализ по выборке внутреннего диаметра Втулки Ø8,5Н14 показывает:
А) Средняя арифметическая = 8,639. Это типичный уровень выборки.
Б) Размах = 0,7, что составляет 8,1 % от среднего значения выборки.
В) Коэффициент вариации=1, 518 % < 33 %, следовательно, выборка однородная.
Г) Коэффициент асимметрии As = — 0,1515, значит левосторонняя асимметрия.
Д) Коэффициент эксцесса Ех = 0,047. Распределение островершинное.
а)
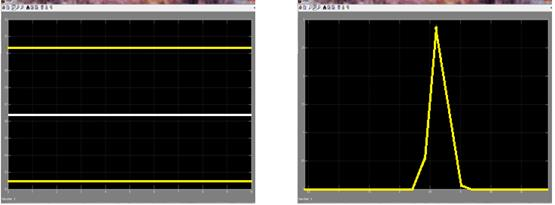
б) в)
Рис. 10. Результаты моделирования схемы (рис. 8) (а) и осциллографов Scope (б), Scope1 (в)
Литература:
1. Кирьянова Г. А., Сорокина Л. А., Кожанова Е. Р. Статистический анализ партии обработанных изделий в MS Excel // Молодой ученый. 2015. № 1 (81). С. 71–73.
2. Кожанов Р. В., Артемова А. Д., Ткаченко И. М., Кожанова Е. Р., Захаров А. А. Построение логических схем с использованием Matlab/Simulink и Scilab/Xcos // Молодой ученый. 2015. № 2. С. 163–167.
