Использование термодинамических моделей для интенсификации процессов флотационной очистки производственных сточных вод

Важными особенностями современного этапа технического прогресса являются все возрастающая сложность внедряемых в производство технологических процессов и значительно ускорившиеся темпы их внедрения.

Существенно сократить сроки освоения новых технологических процессов и снизить затраты на их внедрение позволяют методы математического моделирования [1]. В настоящее время моделирование занимает достойное место в теоретических основах практически всех отраслей промышленности. К числу наиболее быстро развивающихся ее разделов относится моделирование химико-технологических процессов, в том числе процессов очистки природных и сточных вод.

Цель работы

Критический анализ современных математических моделей для описания и изучения процессов флотационной очистки сточных вод, выявление основных факторов, влияющих на эффективность извлечения загрязнений и обсуждение возможных путей оптимизации технологий в зависимости от основных свойств водных систем и режимов работы технологического оборудования

Основная часть работы

При описании процесса флотации дисперсных частиц принято использовать два вида математических моделей.

1.         термодинамические модели, позволяющие оценить вероятность образования флотокомплекса «дисперсные частицы — пузырек воздуха исходя из анализа изменения энергии дисперсной системы

2.         кинетические модели, предусматривающие описание всех стадий образования флотокомплекса дисперсная частица — пузырек воздуха.

Игнорирование кинетики стадии сближения для мелких частиц (менее 10 мкм), являющихся практически безинерционными, не позволяет получить корректные результаты.

Таким образом, исследование кинетики сближения частицы с пузырьком воздуха в теории флотационной очистки нефтесодержащих сточных вод, загрязненных, главным образом, эмульсиями, представляющими собой мелкие безинерционные частицы, имеет решающее значение.

Необходимость изучения кинетики флотации обосновывается более глубоким пониманием явлений, лежащих в ее основе, впервые была отмечена академиком А. Н. Фрумкиным [7]. При этом под кинетикой флотационного процесса следует понимать рассмотрение во времени всех элементарных актов флотации и конечных ее показателей. Особый интерес представляет процесс осаждения частиц на поверхность единичного пузырька, его эффективность, а также скорость флотации коллективом пузырьков. Этим вопросам уделялось значительное внимание уже на ранних этапах развития кинетической теории флотации.

Для вывода уравнения скорости флотации авторами [5] был использован химический закон действия масс

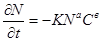,                                                                                                        (6)

где N — счетная концентрация флотируемых частиц, шт/м³;

С — счетная концентрация воздушных пузырьков, шт/м³;

а и в — показатели степени;

К — константа скорости процесса флотации.

Было предложено при оценке физико-химической кинетики процесса флотации не учитывать концентрацию воздушных пузырьков, так как она остается постоянной величиной. Полученное им уравнение скорости флотации имело вид

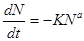,                                                                                                                 (7)

Путем преобразования формулы (7) и ее интегрирования для случая 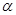=1 была получена формула, описывающая процесс флотации монодисперсных частиц коллективом пузырьков газа

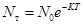,                                                                                                                 (8)

где N₀ и N_т – счетные концентрации флотируемых частиц в начальный момент времени и через Т секунд.

Если вместо значений N₀ и N_т использовать понятие коэффициента извлечения частиц

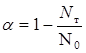
то формула (8) примет вид

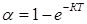.                                                                                                                (9)

Из уравнения (9) следует, что константа скорости процесса флотации имеет размерность величины, обратной времени, с^-1

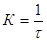,                                                                                                                     (10)

где τ – характерное время очистки сточных вод, в течение которого концентрация флотируемых частиц убывает в е раз.

Таким образом, зная продолжительность процесса флотации Т, начальную и конечную счетную концентрации флотируемых частиц N₀; N_т в соответствии с формулой (10) можно определить

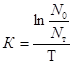.                                                                                                               (11)

В качестве физической интерпретации констант скорости процесса флотации также было предложено рассматривать коэффициент К как произведение вероятности столкновения частиц с пузырьком и вероятности их закрепления на поверхности пузырька.

В работе [5] приводится следующее выражение для определения константы скорости извлечения взвешенных частиц в процессе флотации монодисперсных систем

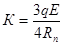,                                                                                                                      (12)

где q – объем газа, поступающего в единицу времени через единицу площади поперечного сечения флотационного объема, м³/м²·с;

R_п – радиус пузырька воздуха, м;

Е – коэффициент эффективности захвата флотируемой частицы пузырьком воздуха.

В связи с тем, что распределение пузырьков по крупности в реальных полидисперсных процессах флотации близко к нормальному, в качестве радиуса пузырьков принимают его среднестатическое значение.

Параметр Е является сложнейшей функцией, зависящей от многих факторов. Известно, что на ход флотационного процесса влияют такие факторы, как род флотируемого материала, размер частиц и пузырьков, электрокинетический потенциал пузырьков воздуха и флотируемых частиц, наличие реагентов и т. д.

Первая попытка определить коэффициент эффективности захвата Е была сделана в работе [3] с опорой на математический аппарат, разработанный в механике аэрозолей

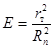,                                                                                                                        (13)

где r_т – максимальный радиус трубки тока, набегающего на пузырек потока жидкости, все частицы из которой задерживаются на поверхности пузырька, м;

Схематично процесс сближения частицы с пузырьком воздуха изображен на рис. 1.

Процессы сближения инерционных (крупных) и безынерционных частиц с поверхностью пузырька имеет качественные различия.

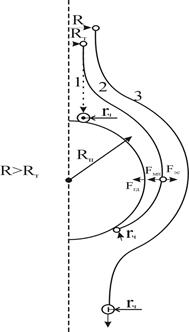
Рис. 1. Траектории сближения флотируемой частицы с пузырьком газа: 1 — траектория инерционной (крупной) частицы; 2 — траектория безынерционной частицы; 3 — траектория безынерционной частицы, находящейся за пределами трубки тока

 

При приближении к поверхности пузырька инерционной частицы ее траектория почти не изменяется, так как силы инерции компенсируют гидродинамическое воздействие потока жидкости, изменяющего свою траекторию вблизи поверхности пузырька газа. Частица движется прямолинейно вплоть до столкновения с поверхностью пузырька воздуха, которое произойдет, если прицельное расстояние 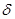(расстояние между проекциями центра пузырька и центра частицы) меньше суммы радиуса пузырька и радиуса частицы.

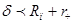.                                                                                                                    (14)

Безынерционные частицы вблизи поверхности пузырька ведут себя иначе. При обтекании поверхности пузырька жидкостью линии тока искривляются, увлекая за собой частицу. Чем меньше размер частицы и разница ее плотности с веществом среды, тем меньше действующие силы инерции и больше приближение ее траектории к траектории линии тока жидкости.

Возможность инерционного осаждения частиц на пузырьке в соответствии с рекомендациями [5] определяется безразмерным параметром

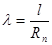,                                                                                                                         (15)

где l – инерционный пробег частицы, м;

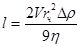 ,                                                                                                                 (16)

где V – скорость движения частицы относительно пузырька, м/с;

Δρ – разность плотностей среды и частицы, кг/м³;

η – динамический коэффициент вязкости среды, Па·с.

Инерционное осаждение возможно, если λ≤λ_кр. В работе [3] для критического значения параметра λ_кр получено число

.

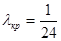Подставив это значение в формулы (15) и (16) можно получить выражение для критического радиуса частицы, ниже которого силы инерции не обеспечивают сближение частицы с пузырьком

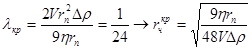.                                                                       (17)

Приняв скорость осаждения частицы равной скорости всплывания пузырька воздуха относительно жидкости, в соответствии с законом Стокса, имеем:

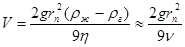,                                                                                   (18)

где 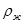– плотность жидкости;

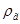 – плотность газа внутри пузырька, кг/м³ (ρ_г<< ρ_ж);

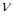– кинематический коэффициент вязкости жидкости, м²/с;

g– ускорение свободного падения, g =9,8 м/с².

Подставляя выражение (18) в (17) имеем

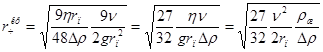.                                                (19)

При радиусе флотируемой частицы превращающим критический радиус 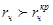имеет место ее инерционное осаждение на поверхности пузырька.

Коэффициент эффективности захвата в элементарном акте инерционного столкновения частицы с пузырьком авторы [5] рекомендуют оценивать по формуле

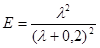                                                                                                         (20)

Если значение Е в формуле (20) близко к единице, то можно считать,

что происходит захват крупных частиц пузырьками по инерционному механизму. Для малых частиц 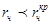 инерционное осаждение невозможно.

В этом случае в соответствии с рекомендациями Е определяется для стоксовского режима всплывания пузырьков воздуха 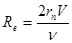<1 по формуле

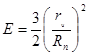                                                                                                            (21)

По некоторым данным формула (21) остается справедливой до Rе<20 [6].

Для режима всплывания пузырьков воздуха, отличного от стоксовского (Rе>1), коэффициент Е определяется по формуле

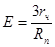.                                                                                                                   (22)

Переходя от счетных концентраций к массовым, в работе [8] приводятся формулы, описывающие кинетику извлечения нефтепродуктов воды при напорной флотации:

-          для флотации пузырьками со средним диаметром менее 80 мкм

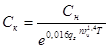,                                                                                                      (23)

где n — счетная концентрация пузырьков во флотаторе, шт/м³;

-          для флотации пузырьками со средним диаметром более 80 мкм.

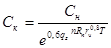,                                                                                                     (24)

где С_н и С_к – начальная и конечная концентрация нефтепродуктов, кг/м³;

q_г – объем газа, поступающего в единицу времени через единицу площади поперечного сечения флотатора, м³/с·м²

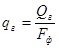,                                                                                                                  (25)

где 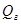– расход газа в выделившихся из раствора при дросселировании пузырьках, м³/с;

F_ф —  площадь поперечного сечения флотатора, м²;

Увеличение коэффициента газонаполнения во флотационном объеме выше определенного критического значения 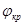 может привести к изменению величины коэффициента эффективности захвата. В работах [2,3] получено выражение для оценки эффективности захвата, которое учитывает не только размеры пузырька, но величину доли диспергированной газовой фазы.

Коллективная скорость всплывания пузырьков газа в жидкости будет отличаться от скорости всплывания одиночного пузырька в свободном объеме. Предположим, что все пузырьки имеют одинаковый размер и строго сферическую форму, а так же, что они равномерно распределены по объему жидкости. В общем случае коллективная скорость всплывания пузырьков жидкости будет зависеть от следующих факторов:

1)        от радиуса одиночного пузырька газа r_п;

2)        от доли диспергированного в жидкости газа 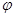 — величины газонаполнения, которая численно равна отношению объема газа к величине объема всей газожидкостной системы.

Используя схему последовательных приближений, с помощью которой краевую задачу можно решить с особой точностью, и рассматривая каждый раз граничные условия только для одного пузырька Кафаров В. В. определил величину скорости его всплытия в виде функции от величины газонаполнения для случая хаотического расположения пузырьков газа [9]

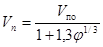, м/с                                                                                                      (26)

где V_п – коллективная скорость всплывания пузырьков газа, м/с;

V_по – скорость всплывания пузырька в неограниченном объеме жидкости, м/с;

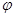– величина газонаполнения.

Применение ячеистой модели к облаку всплывающих в объеме жидкости пузырьков газа позволило получить еще более сложную зависимость

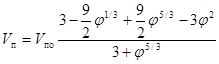, м/с

В работе [9] была сделана попытка оценить влияние наличия дисперсной газовой фазы на вязкость дисперсной системы.

Известно, что дисперсные системы имеют вязкость, превышающую вязкость исходной дисперсной среды. Увеличение вязкости эмульсий и суспензий зависит как от объемной концентрации дисперсной фазы, так и от формы частиц, вязкости их материала, структурообразования и других факторов.

Формула, полученная в [9] имеет вид для определения коэффициентов динамической вязкости смеси.

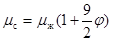
с учетом: 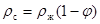 и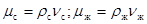

получаем

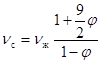
Тогда для случая стоксовского режима всплывания газового пузырька с учетом 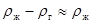 будем иметь

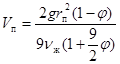, м/с                                                                                                  (27)

Поскольку флотация является сложным физико-химическим процессом, состоящим из следующих стадий: 1) образование флотокомплекса «пузырек воздуха-дисперсная частица»; 2) всплывание флотокомплекса на поверхность жидкости; 3) образование на поверхности жидкости пенного слоя, при описании флотационного процесса необходимо учитывать все эти стадии. В настоящее время создан целый ряд моделей флотационного процесса, учитывающих возможность перехода дисперсных частиц из суспензии в пенный слой и обратно [9]. Прообразом этих моделей флотационного процесса переноса служит обратимая химическая реакция. При этом обратимость проявляется не только на стадии перехода дисперсной частицы из флотокомплекса в пену, но и на стадии образования этого комплекса его всплывания на поверхность жидкости.

Было предложено [10] описывать флотационный процесс системой уравнений, характеризующих переход дисперсных частиц из состояния А (исходное состояние частиц) в состояние В (состояние прилипания и удержания частиц на пузырьке) и далее в состояние С (состояние частицы в пенном слое), при этом предполагается, что на каждой стадии возможны и обратные переходы.

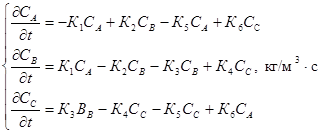                                                       (28)

где С_А; С_В; С_С — соответственно концентрация дисперсных частиц в состояниях А;В и С, [кг/м³];

К₁;К₂;К₃;К₄;К₅;К₆ — константы скорости перехода соответственно из состояния А в состояние В, из состояния В в состояние А; из состояния В в состояние С; из состояния С в состояние В; из состояния С в состояние А; из состояния А в состояние С,

с^-1.

Рассмотренные математические модели были адаптированы для соответствующих авторских технологий флотационной очистки сточных вод при реконструкции флотаторов участка очистка замазученных сточных вод ТЭЦ № 1 г. Пенза [11] и локальных очистных сооружений ОАО «Пензадизельмаш» [4].

Выводы

Проведенный теоретический анализтермодинамических и кинетических процессов флотации позволил сделать следующие выводы:

-          эффективность удаления мелкодисперсных эмульсий примесей зависит от степени дисперсности водовоздушной смеси, а также величины ее газонасыщения, что требует детального экспериментальпо-модельного исследования в каждой конкретной технологической ситуации;

-          повышение эффективности процессов флотационной очистки производственных сточных вод требует, в первую очередь, создания новых технологий генерирования тонкодисперсных водовоздушных смесей с повышенным газонасыщением.

 

Литература:

 

1.         Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры // — М.: ФИЗМАТЛИТ.- 2002. –С. 320.

2.         Дерягин Б. В. Теоретические основы и контроль процессов флотации [Текст] / Б. В. Дерягин, С. С. Духин, Н. Н. Рулев. — М.:Недра. -1980.

3.         Рулев Н. Н. Кинетика флотации мелких частиц коллективом пузырьков [Текст] / Н. Н. Рулев, Б. В. Дерягин, С. С. Духин // Коллоидный журнал. — 1977. –т.39. — № 1.

4.         Гришин Б. М., Андреев С. Ю., Камбург В. Г. Теоретические и экспериментальные исследования флотационной очистки нефтесодержащих производственных сточных вод с применением вихревых смесительных устройств // Региональная архитектура и строительство -Пенза: -2012.- № 1.-С. 11–16.

5.         Дерягин Б. В. Микрофлотация [Текст]/ С. С. Духин, Н. Н. Рулев.– М.:Химия. -1986.

6.         Рулев Н. Н. Теория флотации мелких частиц и флотационной водоочистки [Текст] / Н. Н. Рулев //Дис. канд. хим. наук. — Киев. — 1977.

7.         Фрумкин А. Н. Физико-химические основы теории флотации [Текст] / А. Н. Фрумкин. — М.:АН СССР. -1932.

8.         Стахов Е. А. Очистка нефтесодержащих сточных вод предприятий хранения и транспорта нефтепродуктов [Текст]/ Е. А. Стахов. — Л.: Недра. -1983.

9.         Кафаров В. В. Основы массопередачи.-М.:Высшая школа. — 1976.

10.     Ксенофонтов Б. С. Очистка сточных вод: флотация и сгущение осадков.-М.:Химия. -1992.

11.     Андреев С. Ю., Гришин Б. М. Новая технология безреагентной флотационной очистки сточных вод, содержащих нефтепродукты // Региональная архитектура и строительство -Пенза: — 2011. -№ 1, -С. 36–42.