Рассчитаны температурные зависимости времени релаксации импульса и подвижности носителей в полупроводниках с простой зоной при учете рассеяния носителей тока на пъезоэлектрических колебаниях подрешеток элементарной ячейки кристалла.
The temperature deependencies of pulse relaxation tame end carriers mobility in simplezone semikondaktors are obtained with the accound of skettering the carriers on pizoelektric vibrethons of the sublattices of crustal elementary cell.
В ряде кристаллов без центра инверсии механическая деформация сопровождается их поляризацией и возникновением пъезоэлектрического поля. Последнее приводит к дополнительному механизму рассеяния носителей тока в пъезоэлектрических кристаллах [1]. Для описания этого вида рассеяния введем следующего оператора электрон — фононного взаимодействия
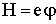, (1)
где е — элементарный заряд (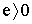
- для дырок, 
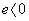- для электронов), 
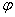- потенциал пъезоэлектрического поля. В дальнейшем предположим, что концентрация носителей тока достаточна мала, т. е. можно пренебрегать эффектами экранирования и пользуясь уравнением Пуассона и линейным соотношением между компонентами векторов электростатистической индукции и напряженности пъезоэлектрического поля нетрудно получить уравнения
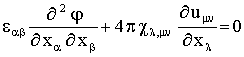, (2)
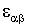-тензор диэлектрической проницаемости кристалла, 
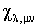- пъезоэлектрический тензор, 
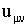- тензор деформации [2], индексы 
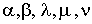— принимают значения 
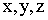, а по повторяющемуся индексам подразумывается суммирование.
Как известно [1–3], связь между компонентами длинноволновой части оператора смещения атомов при оптическом пъезоэлектрическм колебании
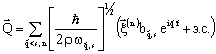, (3)
и тензора деформации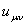 
описывается выражением
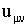
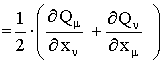, (4)
где 
, 
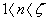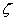- число атомов в элементарной ячейке кристалла, 
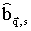и 
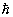
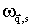- оператор уничтожения и энергия фонона пьезоэлектрического колебания подрешеток друг относительно друга (ветви 
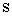с импульсом 
), 
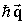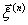-единичный вектор смещения атома с номером 
, 
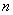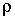- плотность кристалла.
Для удобства видоизменим потенциала 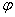как
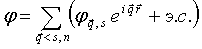, (5)
Тогда подставляя (3) в (4) и полученной в (2) с учетом (5)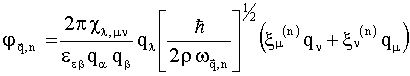 
, (6)
С учетом последнего соотношения перепишем (1) в виде
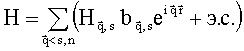, (7)
где 
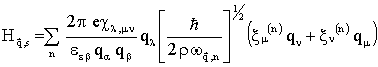, (8)
Отметим, что для кристаллов типа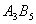 
(кристаллическая симметрия 
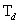), для которых имеется лишь одна отличная от нуля компонента пьезотензора 
(
=
=
=
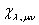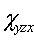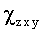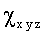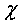), в линейном по 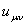и по напряженности электрического поля приближение носители тока взаимодействуются только с поперечными оптическими пьезоэлектричесими фононами. Для гиротропных кристаллов симметрии 
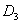(например, теллур) имеет место и взаимодействие носителей тока с продольными оптическими фононами. а для кристалллов, в элементарной ячейке у которых имеется по два атома, (8) перепишем как:
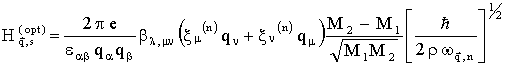, (9)
Время релаксации импульса носителей тока определятся по формуле
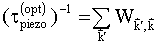, (10)
где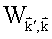 
— вероятность перехода из состояния 
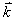в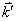 
с испусканием или поглощением оптического фонона, 
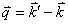— волновой вектор фонона.
В сферическом приближении энергетического спектра носителей тока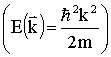 
в кристаллах типа арсенида галлия с простой зоной температурная зависимость время релаксации импульса определяется соотношением;
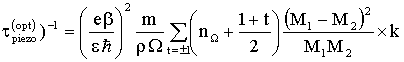, (11)
где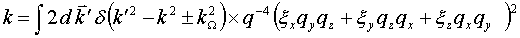 
, 
, 
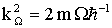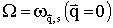— усредненная частота пъезоэлектрических колебаний подрешеток, 
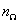— функция распределения оптических фононов, 
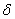-функция описывает закона сохранения энергии.
Отметим, что последний интеграл аналитически не решается и поэтому его будем анализировать в двух предельных областей температур: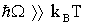 
и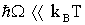 
, 
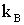-постоянная Больцмана, Т-температура. В этих областях температур имеем: 
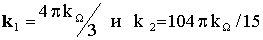соответственно, а время релаксации импульса определяется выражениями [A6]:
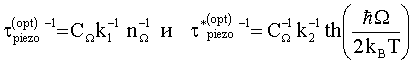, (12)
где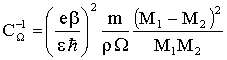 
.
Для полноты задачи ниже приводим выражение для температурной зависимости подвижности носителей тока в рассмотренных нами областях температуры: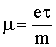 
, где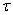 
определяется соотношениями для величин:
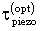и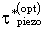 
, где надо произвести замену 
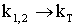. Здесь 
.
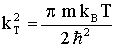Заметим здесь, что определение температурной зависимости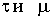 
легко обобщается для изотропного кристалла со сложной зоной. В этом случае при расчетах надо иметь в виду, что и волновые функции носителей тока также зависят от номера ветвей зоны. Также отметим, что этот случай немаловажную роль играет при исследованиях как классических (например, эффект Дембера), так и поляризационных фотогальванических эффектов, последний из которых зависит от состояния поляризации возбуждающего света [4].
Литература:
1. Г. Л. Бир, Г. Е. Пикус. Симметрия и дефармационные эффекты в полупроводниках (Москва, Наука,1972).
2. А. И. Ансельм. Введение в физику полупроводников. (Москва, Наука,1978).
3. В. Л. Бонч- Буревич, С. Г. Калашников. Физика полупроводников. (Москва, Наука,1977).
4. Р. Я. Расулов. Дисс. … д.ф.-м.н. (Санкт- Петербург, 1993),228 с.
