С целью своевременного контроля, и корректировки знаний студентов а также системы контроля хода учебного процесса необходимо создать адаптивные автоматизированные системы управления учебным процессом.
Самым слабым звеном в учебном процессе, как правило, является явно недостаточное количество или иногда полное отсутствие информации у преподавателя о качестве усвоения изучаемого материала, о правильном понимании его, о самостоятельной работе студентов, в частности, предмета основы программирования в начальном курсе обучения. Представление об этом может быть получено лишь в конце обучения, да и то лишь по некоторым курсам и далеко не полное, так как за несколько часов, которые отводятся для оценки знаний преподавателем во время текущего и рубежного контроля с целой группой студентов, трудно выяснить истинные знания, полученные студентами за весь период обучения.
Для более успешного проведения занятий преподаватель должен знать о работе студентов над прочитанным материалом, о качестве его усвоения. Это можно сделать с помощью внедрения современных информационно-коммуникационных, педагогических технологий и моделей обучения в учебный процесс, например созданием системы адаптивного обучения предмета основы программирования на основе нейросетевых технологий.
Специфика подготовки специалиста в области информационной технологии требует создания определенной модели обучения. Под моделью обучения мы понимаем совокупность модели обучаемого, базы знаний предметной области (ПО) и модели концепции обучения [1]. Рассматривая такие области знаний, как математика, информатика, физика, химия и другие естественнонаучные дисциплины, мы сталкиваемся с четко определенными понятиями и правилами ПО, которые характеризуются высокой степенью формализации. Подобные области знаний описывают набором определений, понятий и правил, устанавливающих взаимосвязи между ними. В качестве модели представления знаний таких ПО, нами предлагается семантическая сеть построенная на основе логической граф-структуры дисциплины [2, 3]. Не останавливаясь на процессе логического структурирования предмета информатика и формализации знаний, будем исходить из предположения, что знания уже представлены семантической сетью, узлы которой содержат логически законченные понятия ПО, а дуги — отношения между ними.
Основной особенностью адаптивной системы обучения является оптимизация процесса обучения. На сегодняшний день не существует универсальной методики обучения, поэтому преподаватель выбирает наиболее приемлемый способ обучения исходя из собственного опыта, что не всегда бывает оптимально. Здесь в качестве критерия эффективности мы рассматриваем глубину освоения предмета обучаемым, полноту и прочность усвоенных им знаний, уровень изучения теоретического материала и приобретения практических навыков. Учет в модели компьютеризованной системы обучения свойств самого обучаемого позволяет наиболее эффективно достигнуть поставленной цели обучения. В процессе исследования свойств и характеристик обучаемого нами были выделены следующие параметры, составляющие ядро модели обучаемого (МО): а) тип мышления обучаемого; б) воспринимаемая форма представления знаний; в) свойство уверенности при ответе; г) уровень усвоения знаний обучаемым; д) оптимальная стратегия получения знаний обучаемым.
Воспринимаемая форма представления знаний обучаемым могут быть представлен двумя значениями: интуитивным и теоретически-методологическим мышлением; в редких случаях может быть отнесена только к одному типу. Поэтому для более точного отображения в МО свойств обучаемого предлагается использовать коэффициенты предпочтения для каждого значения параметра. Не снижая общности дальнейших построений, значений таких коэффициентов можно выбирать из отрезка от 0 до 1 (очевидно, что простое нормирование приводит любой набор коэффициентов в отрезок [0,1]). В общем случае значения таких коэффициентов на отрезке [0,1] могут меняться непрерывно, однако, на практике всегда можно считать, что эти значения меняются дискретно с некоторым фиксированным шагом, величина которого определяется с одной стороны семантикой параметра (смысловым содержанием параметра), а с другой стороны требуемой точностью представления в МО свойств обучаемого. Выделим следующие основные, на наш взгляд, формы представления знаний: аналитическая (аналитические выражения, математические модели, алгоритмы, формализованные описания и т. д.), образная (схемы, рисунки, видеофрагменты), эвристическая (практические методы и рекомендации, эвристические описания).
Для представления знаний по определенной теме, например, «Основы алгоритмизации и программирования» предмета «Информатика» выбираем m вопросов. Каждый вопрос объясняем аналитически, либо образно, либо эвристическим путем. Допустим, данный предмет преподает n преподавателей. Для нашего примера возьмем m = 3 вопроса, например, вопрос 1 — алгоритмизация и программирование линейных вычислительных процессов; вопрос 2 — алгоритмизация и программирование разветвляющихся вычислительных процессов; вопрос 3 — алгоритмизация и программирование повторяющихся (циклических) вычислительных процессов; n=2 преподавателя. Введем обозначение: 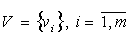 - количество вопросов;
- количество вопросов; 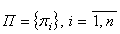 - количество преподавателей; лингвистические переменные соответственно: аналитические
- количество преподавателей; лингвистические переменные соответственно: аналитические
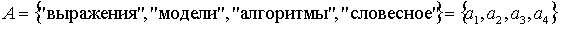 ;
;
логическая функция 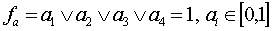 ;
;
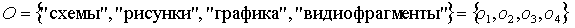 ;
;
логическая функция 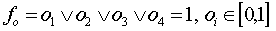 ;
;
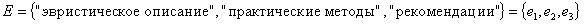 ;
;
логическая функция 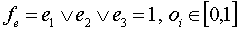 .
.
Кортеж значений параметра форм представления знаний содержит 12 элементов, т. е. 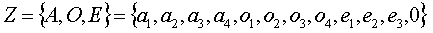 . Первые четыре элемента соответствуют значению коэффициента для аналитической формы представления знаний, следующие четыре — для образной формы и последние четыре — для эвристической. Таким образом, для каждого подкортежа, состоящего из 4 элементов, хотя бы один элемент равен 1, что соответствует некоторому значению коэффициента для каждой формы представления знаний. Например, кортеж (0,0,0,1,1,0,0,0,0,1,0,0) несет следующую смысловую нагрузку: обучаемый в лучшей степени воспринимает практические методы и образную форму (в виде блок-схемы) изучаемого материала, а также ему более доступны словесные описания предлагаемого материала, чем его формальная постановка в виде математических закономерностей. Подобным образом составляются кортежи значений для всех других параметров МО.
. Первые четыре элемента соответствуют значению коэффициента для аналитической формы представления знаний, следующие четыре — для образной формы и последние четыре — для эвристической. Таким образом, для каждого подкортежа, состоящего из 4 элементов, хотя бы один элемент равен 1, что соответствует некоторому значению коэффициента для каждой формы представления знаний. Например, кортеж (0,0,0,1,1,0,0,0,0,1,0,0) несет следующую смысловую нагрузку: обучаемый в лучшей степени воспринимает практические методы и образную форму (в виде блок-схемы) изучаемого материала, а также ему более доступны словесные описания предлагаемого материала, чем его формальная постановка в виде математических закономерностей. Подобным образом составляются кортежи значений для всех других параметров МО.
Объединение кортежей позволяет получить матрицу N x M, где N — это количество параметров МО, а М — длина кортежа значений. Все кортежи необходимо привести к единому значению М, заполнив отсутствующие элементы нулями. Таким образом, мы получаем матрицу, состоящую из нулей и единиц, описывающую состояние модели конкретного обучаемого в некоторый момент обучения.
Предлагаемая адаптивная система обучения, используя сформированную матрицу коэффициентов значений параметров обучаемого должна предложить некоторую эффективную методику обучения. Однако, в процессе обучения, на основе сбора информации о субъекте обучения, происходит изменение МО, что безусловно влияет на методику обучения, которая прежде всего отвечает за формирование предоставляемого обучаемому материала. Задача выбора оптимальной методики обучения сводится к задаче классификации обучаемых, другими словами следует установить соответствие между обучаемым и методикой обучения. При этом, на наш взгляд, важно учитывать не только значения параметров обучаемого в различные моменты времени, но и динамику их изменения. В простейшем случае такую динамику характеризует скорость изменения параметров (производная функции параметра). Другой важный аспект МО, влияющий на эффективность процесса обучения — отношения типа субъект — субъект. Такие отношения, в конечном итоге, определяют взаимовлияние субъектов обучения. Сюда можно отнести конкуренцию, взаимопомощь и т. п.
В качестве математического аппарата, решающего задачу классификации обучаемого нами предлагается нейронная сеть (НС). Нейронные сети достаточно эффективно решают задачу распознавания образов и задачу классификации [4,5]. Рассмотрим процесс проектирования соответствующей НС.
В последние десятилетия интенсивно происходит интеллектуализация многих сфердеятельности, в том числе сферы образования. Одно из направлений — автоматизацияпроцессов обучения и контроля уровня знаний обучаемых в целях, прежде всего, интенсификациипроцесса обучения, повышения качества обучения, коррекции программ обучения.
В исследованиях искусственных нейронных сетей, предназначенных для решениязадач автоматизации обучения и контроля знаний было отмечено, что обобщение опыта обучениялюдей, фактически обладающих биологической нейронной сетью, может дать многоаналогий для организации обучения искусственных нейронных сетей, используемых нетолько в образовательной сфере. При этом, на нынешнем этапе наиболее важнымявляется исследование психолого-педагогических аспектов обучения, имеющихнекоторую аналогию в уже накопившемся опыте обучения искусственныхинтеллектуальных систем, обладающих определенным уровнем интеллекта.
Нейронные сети являются адаптивными обучающимися системами, извлекающими информацию из реальных процессов, которые динамически промоделировать трудно, т. к. они содержат много скрытых неконтролируемых параметров. Применение нейронных сетей позволяет решать задачи, которые трудно или невозможно решать традиционными методами в силу отсутствия формализованных математических описаний процессов функционирования. Нейронные сети в процессе работы накапливают информацию, и эффективность их со временем возрастает. Использование обучаемых нейронных сетей позволяет сделать диагностический контроль объективным и расширить его применение.
Оценка качества обучения имеет как общие закономерности, так и частные — взависимости от конкретной области применения. На первый взгляд, подчеркнем, упрощенный взгляд, наиболее распространенная система оценки качества обучения, является система, в которой решается задача классификации, т. е. отнесение результата к тому или иному классу оценок (например, типичные классы оценок «R1-неудовлетворительно», «R2-удовлетворительно», «R3-хорошо», «R4-отлично»). 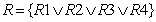 .
.
Проанализировав и перебрав все возможные ситуации, с учетом одинакового принимаемого решения получим систему логических высказываний — предикатов как основу формализации задачи обучения при построении нейросети:
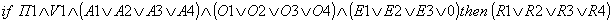 ;
;
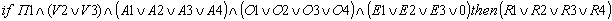 ;
;
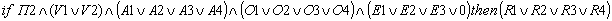 ;
;
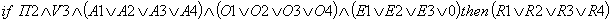 .
.
Тогда, например, первое логическое высказывание означает: «Если преподаватель 1 объясняет вопрос 1 соответственно один из методов аналитического, образного и эвристического представления знаний, то результатом обучения будет решение R1 либо R2, либо R3, либо R4.
Первым шагом здесь является выбор соответствующей модели сети. Мы остановимся на моделях Хопфилда и Хемминга [4, 5]. Эти модели обычно используются для организации ассоциативной памяти. Следующим шагом — является выбор параметров обучения сети. Входной слой НС, в нашем случае соответствует набору параметров обучаемого, представленному матрицей кортежей. Далее следует определить топологию сети, т. е. число элементов и их связи. Здесь мы не будем подробно останавливаться на этом вопросе, так как он подробно освещен в большом количестве публикаций.
Следующий этап проектирования — обучение сети. Типичной формой такого обучения является управляемое обучение [4, 5], когда для каждого набора данных, подающегося в процессе обучения на вход сети, соответствующий выходной набор известен. Данные, используемые для обучения нейронной сети, разделяются на две категории: одни данные используются для тестирования сети, а другие для обучения. Реальные качества нейронной сети выявляются только во время тестирования, поскольку успешное завершение обучения сети должно означать отсутствие признаков неправильной работы сети во время ее тестирования. Процесс тестирования следует реализовать так, чтобы в его ходе для данной сети можно было бы оценить ее способность обобщать полученные знания. Обобщение в данном случае означает способность сети правильно решать задачу с данными, которые оказываются аналогичны данным, предъявлявшимся сети в процессе обучения, но отличными от них.
Рассмотрим подробнее исследуемые нами нейронные сети в применении к задаче адаптивного обучения.
Пусть Х — входной сигнал, Y — выходной сигнал нейронной сети. Необходимо построить отображение X → Y такое, чтобы на каждый возможный входной сигнал X формировался правильный выходной сигнал Y. Отображение задается конечным набором пар (<вход>, <известный выход>). Число таких пар (обучающих примеров) существенно меньше общего числа возможных сочетаний значений входных и выходных сигналов. Совокупность всех обучающих примеров носит название обучающей выборки. В задаче компьютеризованного адаптивного обучения Х — набор параметров модели обучаемого, Y — код, определяющий методику обучения, соответствующую текущим значениям параметров МО.
В нейронной сети, основанной на модели Хопфилда, Х — набор параметров, представленный матрицей (N×M) конкретного обучаемого. Следовательно, количество нейронов в сети — Т = N*M. Y — представляет собой образец матрицы (N×M), соответствующей одной из методик обучения. Известно, что сеть Хопфилда при наличии Т нейронов способна запомнить примерно 0,15*Т образцов. В нашем примере Т = 5*12 = 60, и, следовательно, количество образцов равно 9, что позволяет использовать достаточное количество разнообразных методик в процессе обучения. Недостатком сети Хопфилда является то, что на выходе сети получается сам образец, характеризующий методику обучения, что в нашем случае избыточно, достаточно лишь выявить тип рекомендуемой методики. Другим недостатком является большое число нейронов сети, что может влиять на время получения результирующего решения сети. Программная реализация сети Хопфилда обеспечивает эксперимент с параметрами модели обучаемого и определением соответствующих методик обучения.
В нейронной сети Хемминга входные сигналы Х соответствуют набору параметров обучаемого, количество входных сигналов — Т = N*M. Число нейронов сети равно числу образцов, т. е. числу предлагаемых методик. Выходные сигналы Y соответствуют образцам и представляют собой вектор с одним единичным значением. Сеть Хемминга решает задачу классификации, т. е. соотносит входные сигналы с одним выходным сигналом. Недостатком сети является удачное распознавание только слабо зашумленных наборов входных сигналов.
Практическая реализация сетей обеих моделей позволяет в ходе эксперимента выяснить следующее: какая модель точнее решает задачу выбора предпочтительной методики обучения на основе параметров МО; какой параметр МО несет определяющее влияние при выборе методики обучения; каким образом сеть обрабатывает тупиковые ситуации, т. е. ситуации, в которых невозможно распознать предлагаемый входной набор.
Итак, модели НС Хопфилда и Хемминга позволяют выделить наиболее эффективную методику обучения для конкретного субъекта обучения. Авторами ведется эксперимент, в рамках которого строятся модели обучаемых — студентов 1, 2 курса специальностей «прикладная математика и информатика», «математика», «физика» Ургенчского государственного университета. Не меньший интерес в реальном учебном процессе представляет использование такой модели нейронной сети как многослойный персептрон. Основным применением этой модели является решение задачи прогнозирования. Например, с использованием модели многослойного персептрона можно решать задачу построения прогноза сдачи сессии студентами некоторой группы. В качестве априорных данных для обучения сети используется информация о сдаче этой группой предыдущих сессий, о сдаче этой сессии другими группами прошлых лет.
Результаты рассмотренной модели обучения субъекта на основе нейросетевых технологий могут быть использованы:
- Для построения адаптивных компьютерных обучающих и контролирующих систем (АКОС);
- Для более глубокого понимания и дальнейшего развития теории построения и обучения искусственных нейронных сетей;
- Для более широкого внедрения нейронных технологий в вузовскую систему обучения, в частности, для прогнозирования уровня знаний, умений, навыков студентов по конкретным предметам, направлениям специальностей, что позвольяет своевременно внести соответствующие корректировки методики обучения в целом.
Литература:
1. Кольцов Ю. В., Добровольская Н. Ю., Подколзин В. В. Метамодель компьютерной системы обучения. //Современные проблемы школьной и вузовской педагогики. Краснодар, КубГУ, 1998.
2. Юсупов Ф., Юсупов Д. Ф., Раззаков Б. Повышение эффективности изучения курса информатика на основе структурно-логической граф схемы дисциплины/ Высшее образование сегодня. — М.: 2011, № 11. — С. 46–49.
3. Ермаков А. В. Методика обучения структурированию учебной информации как основа управления учебно-познавательной деятельностью учашихся на уроках физики/А. В. Ермаков, О. В. Аквилева//Матереалы по теории и методике обучение физике. Вып, 9. — Н.Новгород: НГПУ, 2007. — с. 43–46.
4. Рудковская Д., Пилиньский М., Рудковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. — М.: Горячая линия. — Телеком, 2006. — 452 с.
5. Барский А. Б. Нейронные сети: распознавание, управление, принятие решений. — М.: Финансы и статистика, 2004.—176 с.







