В последние десятилетия в наиболее развитых мировых экономиках происходит усложнение механизмов перераспределения финансовых ресурсов. Вследствие этого, наблюдается резкое повышение активности портфельного инвестирования на финансовых рынках. Фондовый рынок испытывает подъемы и падения под влиянием разного рода экономических и политических, внутренних и внешних факторов. Ситуация на фондовых рынках нестабильна и весьма рискованна для большого числа инвесторов. Для финансовой деятельности важно не избегать риска, а иметь возможность его предвидеть и снизить. Принятие инвестиционных решений основано на максимизации доходности и минимизации риска вложений. Портфельное инвестирование опирается на принцип диверсификации, подразумевающий распределение капитала между различными активами. Для достаточно крупных сумм вложений такой подход наиболее предпочтителен, поскольку важно ограничить риски, которым подвержены инвестиции.
В данной статье проанализируем существующие теоретические подходы к проблеме формирования оптимального портфеля на фондовом рынке.
Начало исследований в области моделей портфельного инвестирования было положено Г. Марковицем в 1952 году в статье «Выбор портфеля». За этот труд автору в 1990 году была вручена Нобелевская премия по экономике [6]. Будущий доход рассматривается Марковицем как случайная переменная. То обстоятельство, что доход, ожидаемый от приобретения инвестором различных видов активов, является случайной величиной, обуславливает существование такой категории, как риск. Риск актива (портфеля) — это вероятность неполучения ожидаемой доходности в требуемом размере, степень отклонения фактически полученной доходности от ожидаемой, определяется как дисперсия или стандартное отклонение случайной величины. Именно Г. Марковиц впервые предложил рассматривать задачу формирования портфеля с учетом не только доходности, как это делалось ранее, но и риска. Однако риск в модели Марковица оценивается при помощи стандартного отклонения, которое не учитывает асимметричность распределения доходности портфеля, а также «тяжелые хвосты».
Продолжил исследование портфельной теории в конце 50-х — начале 60-х годов 20 в. Дж. Тобин. Автор преобразовал модель Г. Марковица за счет введения в портфель безрискового актива и возможности заимствования. Инвестор имеет возможность привлекать дополнительные заемные средства для увеличения своих вложений в портфель, составленный из рисковых, имеющих более высокую доходность, активов. В качестве безрискового актива принимается любой вид актива (денежная ссуда, облигация и т. п.), имеющий ненулевую гарантированную доходность, равную, как правило, ставке процента. Результатом исследований является вывод, что вне зависимости от предпочтений инвесторов, структура оптимального портфеля, состоящего только из рисковых активов, является одинаковой для всех инвесторов при наличии на рынке безрискового актива. Структура же вложений инвесторов — разная, в зависимости от отношения к риску и предпочтений относительно доходности и риска.
В 1960-х годах У. Шарп предложил индексную модель оценки капитальных вложений финансовых активов (Capital Asset Pricing Model, CAPM) [7]. Модель CAPM имеет вид:
,
где 
— ожидаемая доходность актива,
— часть доходности актива, полученная в отсутствие воздействия на него рыночных факторов. Она зависит от индивидуальных характеристик актива, не учитываемых рынком.
— ожидаемая доходность рыночного портфеля,
— коэффициент рыночного риска, показатель чувствительности доходности актива к изменению доходности рынка,
– часть общей доходности актива, обусловленной влиянием рыночных факторов,
– независимая случайная переменная, отражающая влияние специфического (нерыночного) риска данного актива на величину его ожидаемой доходности.
С 1964 года появляются другие работы, связанные с моделью оценки доходности активов CAPM. Труды Шарпа (1964), Линтнера (1965), Моссина (1966) были посвящены одному и тому же вопросу: определению соотношения между доходностью и риском актива при равновесии на рынке. При выборе оптимального портфеля инвестор учитывает не «весь» риск, связанный с активом, а только его часть, называемую систематическим (рыночным), или недиверсифицируемым риском. Эта часть риска актива тесно связана с общим риском рынка в целом и количественно выражена коэффициентом «бета», введенным Шарпом в его однофакторной модели. Остальная часть (так называемый несистематический, или диверсифицируемый риск) ликвидируется диверсификацией портфеля. Характер связи между доходностью и риском имеет вид линейной зависимости, и, тем самым, обычное практическое правило «большая доходность — большой риск» получает точное аналитическое представление.
Таким образом, развитие портфельной теории можно условно разделить на следующие этапы. На первом этапе осуществлялась разработка математических основ для портфельной теории (Г. Марковиц). На втором этапе — создание теории рыночного портфеля за счет введения в портфель безрискового актива и возможности заимствования (Дж. Тобин). Третий этап — активное развитие теории оптимального портфеля (У. Шарп, Я. Моссин, Дж. Линтнер, М. Миллер, Ф. Модильяни, Ф. Блек, М. Шоулз, Р. Мертон и др.). На данном этапе развивается математическая теория (B,S)-рынков, в которой рассматриваются портфели, состоящие из рискового (S) (акции, валюта) и безрискового (B) (банковский счет) активов (Harrison J. M., Kreps D. M., Pliska S. R., Dalang R., Morton A., Willinger W., Föllmer H., Leukert P., Sondermann D., Schweizer M., Schäl M., Duffie D., Richardson H. R., Ширяев А. Н., Мельников А. В., Кабанов Ю. М., Крамков Д. О., Нагаев А. В., Павлов И. В., Белявский Г. И., Демин Н. С. и др.). Модели (B,S)-рынков широко применяются на практике как инструментарий для определения «справедливой» цены опциона.
В настоящее время широко используется еще один из подходов формирования портфеля с учетом показателя рисковой стоимости VAR (Value at Risk) — «стоимость под риском».
VAR — это мера риска, которая показывает, на какую максимальную сумму денег может понизиться стоимость портфеля инвестора в течение определенного периода времени с заданной доверительной вероятностью [2].
Существуют разные методики определения VAR. Их можно разделить на две группы: параметрические (аналитические или дисперсионно-ковариационные) и непараметрические модели. Модель называется параметрической, если известна функция распределения случайной величины и параметры ее распределения. В параметрической модели VAR предполагается, что доходность финансовых активов следует определенному виду вероятностного распределения, обычно нормальному. При использовании прошлых статистических данных, определяют ожидаемые значения доходностей, дисперсий и ковариаций доходностей активов. На их основе рассчитывают VAR портфеля для заданного уровня доверительной вероятности по следующей формуле [2]:
;
где 
— VAR портфеля;
— стоимость портфеля;
— стандартное отклонение доходности портфеля, соответствующее времени, для которого рассчитывается VAR;
— количество стандартных отклонений, соответствующих уровню доверительной вероятности 
.
В [4] автор предлагает непараметрическую методику формирования портфелей, выдвигая предположение, что между двумя активами в портфеле существует непараметрическая связь. Непараметрический метод расчета VaR избегает привязки к какому-либо виду распределения. В качестве коэффициента непараметрической связи можно взять коэффициент Кендалла, ранговый коэффициент Спирмена. Тогда мера риска, рассчитанная по методике непараметрического портфеля, имеет вид:
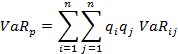
где
– произведение матриц вектора и столбца весов активов на квадратную матрицу 
.
Недостатком непараметрического метода является использование прошлых данных, которые могут внести статистическую ошибку.
Показатель меры риска VAR и его различные модификации рассматриваются в исследованиях Е. М. Бронштейна, И. В. Демина, А. С. Дорохова, Ю. Б. Кисилевича, О. Л. Крицкого, Ю. В. Куреленковой, А. А. Лобанова, Т. С. Ткаченко, А. А. Уфимцева, М. К. Ульяновой, А. М. Шапошниковой и других.
Методология VAR является весьма популярной, так как обладает рядом преимуществ, в отличие от других средств управления риском [1]:
- позволяет измерить риски на различных рынках универсальным образом;
- позволяет измерить риски как возможные потери, соотнесенные с вероятностями их возникновения;
- позволяет агрегировать риски отдельных позиций в единую величину для портфеля, учитывая при этом информацию о количестве позиций, волатильности на рынке.
Однако методология VAR применима к стабильным рынкам и перестает адекватно отображать величину риска, когда происходят резкие изменения. Если рыночные условия существенно изменяются, например, скачкообразно изменяются цены, резко изменяется ликвидность рынка или корреляция между активами, то VAR учтет эти перемены через определенный промежуток времени, только накопив необходимую статистику событий данных [1].
В работе [3] рассматриваются когерентные меры риска и обобщенные когерентные меры риска. Достоинством обобщенных когерентных мер является то, что они точнее описывают реальные стратегии капиталовложений. Однако, в отличие от когерентных мер, они не позволяют оценить риск приемлемых портфелей, а также являются сложными в расчетах.
В последние десятилетия при анализе фондовых рынков, в том числе для решения задач портфельной оптимизации, стали использоваться элементы искусственного интеллекта: теория нечётких множеств [5,9,10,11,12,13,14] и нечёткая логика [14], нейронные сети [14], генетические алгоритмы [13,14]. Это позволяет учитывать при расчётах неопределённость внешней среды, получать в приемлемые сроки решение оптимизационных задач большой размерности с достаточно высокой точностью. Некоторые исследователи считают целесообразным учитывать в модели портфельной оптимизации третий важный критерий, кроме риска и доходности, — их ликвидность [8].
В настоящее время существует большое количество научных трудов отечественных и зарубежных авторов, посвященных проблеме формирования портфеля, снижению рисков, связанных с инвестиционной деятельностью, и выбора как отдельно взятых активов или портфелей, так и инвестиционных стратегий в целом.
Литература:
1. Александрова Е. Б. Методы оценки риска в строительстве — Экономическое возрождение России, г.Санкт-Петербург. [Электронный ресурс]: Режим доступа URL: http://ekvr.narod.ru/management12.htm.
2. Буренин А. Н. Управление портфелем ценных бумаг. — М.: Научно-техническое общество имени академика С. И. Вавилова, 2007.
3. Воробьев О. Ю., Мартынова Т. А., Новоселов А. А. Модифицированные когерентные меры риска (для евклидовой нормы). Вестник КрасГУ, 2005, N4, с. 183–188.
4. Кирьянов, И. В. Методика формирования непараметрических портфелей // Сибирская финансовая школа, 2011. — № 2. — с. 78–83.
5. Недосекин А. О. Нечётко-множественный анализ риска фондовых инвестиций. — СПб., 2002. — 181 с.
6. Шапкин А. С., Шапкин В. А. Управление инвестиционным портфелем ценных бумаг. — М.: Издательско-торговая корпорация «Дашков и Ко», 2007г. — 512с.
7. Шарп У., Александер Г., Бэйли Дж. — ИНВЕСТИЦИИ: Пер. с англ. — М.: ИНФРА-М, 2001.
8. Arenas Parra M., Bilbao Terol A., Rodrígues Uría M. V. A fuzzy goal programming approach to portfolio selection // European Journal of Operational Research. — 2001. — № 133. — P. 287–297.
9. Chang T. J., Meade N., Beasley J. E., Sharaiha Y. M. Heuristics for cardinality constrained portfolio optimization // Computers & Operational Research. — 2000. — № 27. — P. 1271–1302.
10. Carlsson C., Fullér R., Majlender P. A possibilistic approach to selecting portfolios with highest utility score // Fuzzy Sets and Systems. — 2002. — № 131. — P. 13–21.
11. Grishina Е. N. On One Method of Portfolio Optimization With Fuzzy Random Data // International Conference on Fuzzy Sets and Soft Computing in Economics and Finance (FSSCEF 2004): Proceedings. — Saint-Petersburg, 2004. — Vol. 2. — P. 493–498.
12. Sewastianow P. and Jonczyk M. Comparative Study of Aggregation Methods in Bicriterial Fuzzy Portfolio Selection // International Conference on Fuzzy Sets and Soft Computing in Economics and Finance (FSSCEF 2004): Proceedings. — Saint-Petersburg, 2004. — Vol. 2. — P. 484–492.
13. Uryasev, S., Optimization Using CVaR: Algorithms and Applications, Stochastic Optimization Lecture Notes 7, University of Florida, USA
14. Yazenin A. V. Optimization with Fuzzy Random Data and its Application in Financial Analysis // International Conference on Fuzzy Sets and Soft Computing in Economics and Finance (FSSCEF 2004): Proceedings. — Saint-Petersburg, 2004. — Vol. 1. — P. 16–32.
