Статья посвящена проблеме развития творческой активности учащихся в процессе обучения геометрии в подростковом возрасте. Автор дает определение творческой активности, раскрывая понятия творчества и активность. Разрешение проблемы развития творческой активности автор видит в процессе внеклассной работы. С применением информационных технологий. Рассмотрены возможные применения обучающих программных средств на внеклассных занятиях.
Ключевые слова: творчество активность, творческая активность, информационные технологии.
The article is devoted to the development of creative activity of students in learning geometry. The author defines creativity, revealing the concept of creativity and activity. Resolution of the problem of creative activity the author sees in extracurricular activities. With the application of information technology. Consider the use of educational software for school activities.
В настоящее время современному обществу нужны выпускники школ имеющих нестандартный взгляд на проблемы, владеющих умениями исследовательской работы, способных к слиянию собственных сил с силами общества в рамках сложившегося исторического контекста, способных к творчеству.
Указанные требования зафиксированы в ФГОС второго поколения среднего образования «развития личности, способностей, удовлетворения познавательных интересов, самореализации обучающихся, в том числе талантливых, через организацию урочной и внеурочной деятельности, социальной практики…», [1] а так же на Стандарт ориентировано становление личностных характеристик, включающим, готовность и способность обучающихся к саморазвитию и личностному самоопределению.
В национальной образовательной инициативе «Наша новая школа» отмечается, что главной задачей современной школы является раскрытие способностей каждого ученика, воспитание порядочного и патриотичного человека, личности, готовой к жизни в высокотехнологичном, конкурентном мире. Одним из путей повышения качества образования является развитие познавательных, интеллектуальных и творческих способностей школьников, развитие творческой активности учащихся.
Проблема развития творческой активности личности относится к разряду наиболее актуальных тем. Это обусловлено тем, что в современных социально-экономических условиях человек вынужден все чаще решать нестандартные задачи и активно влиять на окружающую его среду.
Развитию теории и практики формирования творческой активности школьников способствовали исследования отечественных ученых: В. В. Афанасьева, В. И. Андреева, Л. С. Выготского, В. А. Гусева, А. Л. Жохова, И. Я. Лернера, А. М. Матюшкина, Г. И. Саранцева, Е. И. Смирнова, М. А. Холодной, А. В. Хуторского, В. Д. Шадрикова, Д. Б. Богоявленской и др.
В педагогической науке существуют разные взгляды на определение творческой активности.
Для определения творческой активности рассмотрим понятия «активность» и «творчество».
Активность человека, по мнению М. С. Кагана, [3] «призвана обеспечить не только его биологическую, но и его социальную жизнь». В теории личности А. Ф. Лазурского [4] человек выступает как активный деятель в окружающей среде. Под «средой» автор понимает не только вещи, природу, людей, «человеческие взаимоотношения, но также идеи, духовные блага, эстетические, моральные и религиозные ценности и т. п».. Активность выступает важнейшей характеристикой качества личности и ее деятельности, которая становится одной из основных предпосылок достижения целей обучения и воспитания, общего и профессионального развития личности человека. Важную роль в процессе становления человека как активного деятеля играют, согласно А. Ф. Лазурскому, процессы воспитания и образования, в ходе которых природные задатки человека могут быть преобразованы в личностно и социально значимые качества личности. А. Н. Леонтьев видел внутриличностные источники активности в потребностно-мотивационной сфере. Близкую точку зрения на сущность феномена активности мы находим и в работах Б. Ф. Ломова. В психологическом аспекте, считает он, активность может рассматриваться как осуществление высших жизненных потребностей личности, к которым он относит стремление занять определенную позицию в обществе, получить общественное признание, обеспечить самовыражение и т. п. Он отмечает: «Активность есть особое качество субъекта деятельности, состоящее в интеграции его психологических возможностей, способностей, знаний и их направленности на достижение цели».
Вопросы о сущности творчества ставились многими научными школами. Дружинин В. Н. [2] определяет творчество как деятельность, результатом которой является создание новых, оригинальных идей, более совершенных материальных и духовных ценностей, обладающих объективной и субъективной значимостью.
В. А. Далингер [1] понимает творчество, как целенаправленную теоретическую и практическую деятельность человека, которая приводит к созданию новых гипотез, теорий и методов.
Таким образом, под творческой активностью можно понимать объединённые в группу личностные качества индивида, которые обуславливают внутреннюю потребность, тенденцию к эффективному творческому процессу, к самовыражению относительно внешнего мира. Творческая активность — это устойчивое интегративное качество, одновременно присущее и самой личности, и её деятельности, выражающееся в целенаправленном единстве потребностей, мотивов, интересов и действий, характеризующееся осознанным поиском творческих ситуаций.
Развитие творческой активности — это процесс и результат качественного изменения личности, увеличение комплекса качеств, характеризующих ее творческую активность, происходящее за определенное время посредством общения, обучения, воспитания и самовоспитания.
Одним из основных показателей творческой активности является самостоятельность. Развитие самостоятельности в указанном стандарте [6] среди общих учебных умений, навыков и способов деятельности выделено творческое решение учебных и практических задач: умение мотивированно отказываться от образца, искать оригинальное решение; самостоятельное выполнение творческих работ, участие в проектной деятельности. В этом процессе неоценимую роль играет изучение математики, а в частности в изучении элементов геометрии на ранних этапах обучения.
Особо значимо развитие творческого потенциала человека в период социализации и становления личности, а именно в подростковом возрасте. Подростковый возраст с 11до 14 лет считается критическим периодом развития. Л. И. Божович связывает возникновение данного кризиса с тем, что быстрый темп физического и умственного развития создает предпосылки для образования таких потребностей, которые не могут быть удовлетворены в условиях недостаточной социальной зрелости школьников этого возраста [2. С. 105].Л. И. Божович полагает, что кризис подросткового возраста связан с возникновением в этот период нового уровня самосознания, характерной чертой которого является появление у подростка способности и потребности познать самого себя как личность, обладающую именно ей, в отличие от всех других людей, присущими качествами.
В связи с этим с 7-го класса начинается резкое расслоение коллектива учащихся: на тех, кто легко и с интересом усваивают программный материал по математике, на тех, кто добивается при изучении математики лишь удовлетворительных результатов, и тех, кому успешное изучение математики дается с большим трудом. Все это приводит к необходимости индивидуализации обучения математике, одной из форм которой является внеклассная работа.
Внеклассная деятельность представляет собой возможность развития творческой активности школьников, которая в совокупности с воспитательным воздействием, развивает личностные качества. Реализацию развития творческой активности необходимо осуществлять на протяжении всего процесса обучения математики. Однако в процессе классных занятий, ограниченных рамками учебного времени и программы, это не удается сделать с достаточной полнотой.
На сегодняшний день определенных программ по геометрии во внеклассной деятельности для развития творческой активности не существует. Для учителей возникает новая задача в разработке определенных занятий, подбор различных дидактических средств.
Одним из направлений формирования творческой активности учащихся, во внеклассной работе по геометрии, может стать применение возможностей информационно-коммуникационных технологий.
Понятию «информационные и коммуникационные технологии» различные авторы дают неоднозначную интерпретацию. Автор опирается на определение, представленное в государственном стандарте «Информационно — коммуникационные технологии в образовании», в котором отмечено, что под информационно-коммуникационными технологиями необходимо понимать — информационные процессы и методы работы с информацией, осуществляемые с применением средств вычислительной техники и средств телекоммуникаций. Внедрение ИКТ открывает принципиально новые возможности для развития творческой активности школьников. Использование ИКТ на внеклассных занятиях по математике — одно из средств формирования коммуникативных навыков учащихся, позволяющее интенсифицировать образовательный процесс, активизировать творческую деятельность учащихся, увеличить эффективность занятия.
Говоря о существующих методических разработках, относящихся к использованию ИКТ во внеклассной работе по математике, необходимо отметить разрозненность накопленного материала, охватывающего лишь некоторые ее направления. Рассмотрим несколько примеров:
Использование обучающих программных средств по математике для устранения пробелов в знаниях школьников.
Применение средств, изначально не предназначенных для решения математических задач, во внеклассной работе по математике, использующих в основном различные редакторы изображений — «Paint Illustrator» и т. п. для построения всевозможных чертежей. Примером может служить применение этих программ при изучении паркетов, предложенное И. М. Смирновой и В. А. Смирновым [5].
Сюда же можно отнести использование программы «Power Point» для демонстрации излагаемого на внеклассном занятии материала или заданий какого-либо конкурса.
Решение на внеклассных занятиях математических задач с использованием языков программирования «Живая математика», «Pascal», «Delphi», «Basic» и т. п.
На внеклассных занятиях в школе можно использовать специализированные математические пакеты «Maple», «MathCAD», «Derive», «Mathematica» и т. п. для решения различных математических задач.
Приведем пример поэтапного изучения темы «Геометрические преобразования и паркеты» на внеклассных занятиях по геометрии с использованием программы Paint, направленной на развитие творческой активности.
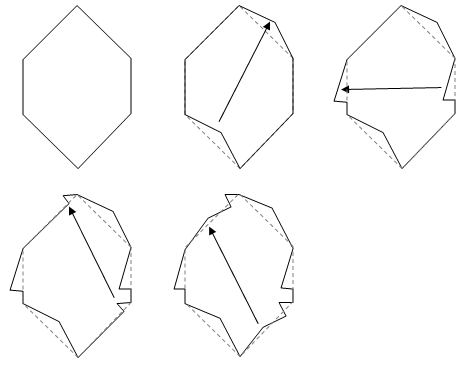
1 этап. Ознакомление с основными способами построения простых правильных геометрических паркетов. Приводятся образцы некоторых из них.(рис.1)
На этом этапе учитель знакомит учащихся с элементарными формами познавательной деятельности, сообщая математические сведения, разъясняя, как можно было бы получить их самостоятельно. С этой целью он использует лекционную форму работы или рассказ, а затем организует самостоятельную деятельность учеников, состоящую в изучении доступного материала учебного пособия и решении задач, предварительно разработанных учителем в качестве примеров.
Рис. 1.
2 этап. Ознакомление построения правильных паркетов в программе Paint. Строя разнообразные выбранные более понравившиеся паркеты в программе, учащиеся не только знакомятся с технологией построения паркета, но и обобщают материал о свойствах многоугольников, рассматривают различные возможные комбинации из геометрических фигур.(рис.2)
Рис. 2.
3 этап. Введение элемента творчества. Составление шаблона одной ячейки взяв за основу правильный многоугольник, на основе построения орнаментов созданных Эшера. Необходимо разобраться, как Эшер создавал свои орнаменты, на примере. Вырезая, «кусочек» плоскости из внутренней области этой фигуры, то такой же надо добавить снаружи. Рассмотрим пример головы женщины. (рис.3)
Рис. 3.
На домашнее задание предложить учащимся придумать собственный шаблон.
4 этап. Построение собственного творческого паркета в программе.
Ребята, которые составили собственный шаблон, строят свой собственный, а кто не составил, тот составляет предложенный учителем, но обязательно с учетом введения нового недостающего элемента в паркете. Например сделать не кошку, зайчика, изменив структуру уха. Формируя, самостоятельность на данном этапе учащиеся применяют оригинальные и нестандартные решения данной задачи, развивая воображение и мышление.
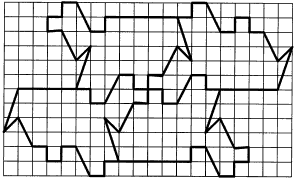
5 этап. Познакомить с новыми способами построения паркета с помощью прямоугольной системы координат, центральной симметрией и поворотов. (рис.4)
Рис. 4.
Рис. 5.
На рис.5, паркет может быть совмещен сам с собой разными параллельными переносами, например, на три клетки вправо и на одну клетку вверх. Этот параллельный перенос задается парой чисел (3; 1). Данный паркет также совмещается сам с собой параллельным переносом, который характеризуется парой чисел (- 6; — 2), или (- 2;3).
Н данном этапе необходимо привлечь учащихся к обсуждению различных способов решения познавательной задачи и отбору наиболее рационального из них; поощрять самостоятельную деятельность учеников в сравнении способов. Познакомить учащихся с общими и частными указаниями, содействующими самостоятельному выбору путей решения познавательной задачи.
6 этап. Оформляется стенд собственных геометрических паркетов. Учащимся предлагается написать собственный проект. Предлагаются темы: «Дворцовые паркеты», «Геометрические преобразования», «Орнаменты и бордюры» и т. д.
Внеклассные занятия по математике призваны решить целый комплекс задач, по углубленному математическому образованию, всестороннему развитию индивидуальных способностей подростков и максимальному удовлетворению их интересов и потребностей. На внеклассных занятиях у учащихся развиваются коммутативные навыки, они не боятся рассуждать и выдвигать гипотезы, активно участвуют в дискуссии.
Применения ИКТ стимулируют творческий потенциал учеников, способствуют развитию навыка видеть, формулировать и понимать геометрические закономерности, увеличивают степень эмоциональной вовлеченности и запоминаемости изучаемого материала.
Внеклассная работа представляет собой возможность развития творческой активности школьников, которая в совокупности с воспитательным воздействием, развивает личностные качества.
Литература:
Далингер, В. А. Самостоятельная деятельность учащихся и ее активизация в процессе обучения математике. Омск: Изд-во ОмИПКРО, 1993. — 156с.
Дружинин, В. Н. Психология общих способностей [Текст]/ В. Н. Дружинин. — М.: ИЦ «Академия», 1996
Каган М. С. Человеческая деятельность / опыт системного анализа. — М.:Политиздат,1974. 328с.
Лазурский А. Ф. Избранные психологические труды по общей психологии. –М.: Наука, 1997. 446с
Смирнов, В. А. Компьютер помогает геометрии // Математика. 2003. № 21. С. 44–45.
Федеральный государственный стандарт основного общего образования [Электронный ресурс]– Режим доступа: http://standart.edu.ru/catalog.aspx?CatalogId=2588