Вся информация, получаемая нами из внешнего мира, проходит определённые стадии обработки, главной из которой является анализ. Для подготовки сигнала к анализу необходимо применить первичную обработку для того, чтобы сделать возможным использование стандартных алгоритмов анализа. Часто первичная обработка может занимать большее количество времени, чем анализ. Например, для решения финансовых задач более 90% вычислительного времени уходит на первичную обработку [8].
Первичную обработку определяют как преобразование входного сигнала в форму, пригодную для подачи на вход стандартному алгоритму. Целью предварительной обработки могут быть уменьшение размерности или сложности задачи [8]. Рассмотрим предварительную обработку сигнала при помощи вейвлетов. Вейвлеты в таком применении помогают решить ряд задач, к примеру, сжатие данных [2], выявление особенностей [7], моделирование [9], удаление зашумлённости. Среди приложений, использующих первичную обработку вейвлетами есть сигнализаторы пожара [8], выявление особенностей сейсмических волн [1], компрессия данных [4], обработка данных ЭКГ [5], распознавание клеток крови [3] и др. Как правило, первичная обработка вейвлетами позволяет произвести выбор некоторого числа значащих вейвлетных коэффициентов, к которым в дальнейшем применяются стандартные методы обработки.
Сначала определим различие между алгоритмом классификации и кластеризации. Классифицирующий алгоритм можно представить в виде отображения 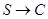 , где
, где 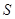 - это множество входных сигналов, а
- это множество входных сигналов, а 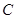 - множество классов. Кластеризация кроме такого отображения строит ещё и само множество классов.
- множество классов. Кластеризация кроме такого отображения строит ещё и само множество классов.
Существует большое количество стандартных алгоритмов классификации и кластеризации. Но точность и скорость вычисления зависит не только от самого алгоритма, но и от данных. Как уже говорилось, вейвлет-анализ помогает уменьшить размерность задачи. Но кроме уменьшения размера входных данных, вейвлет-анализ помогает выявить ещё и особенности сигнала. Для этих задач используется алгоритм выбора наилучшего базиса [6].
Прежде всего, нужно осуществить вейвлет-разложение и получить соответствующие коэффициенты (или дерево разложения). Выбор наилучшего базиса проходит по следующей схеме:
Начиная с предпоследнего уровня:
1. Подсчитаем значение стоимостной функции узла (F)
2. Сравниваем F данного узла с суммой стоимостных функций дочерних узлов (F и F
и F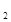 )
)
3. Если F < F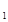 + F
+ F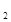 , то F включается в число выбранных узлов (при этом всё поддерево под этим узлом исключается из списка выбранных)
, то F включается в число выбранных узлов (при этом всё поддерево под этим узлом исключается из списка выбранных)
4. Иначе F = F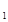 + F
+ F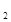
Как видно из алгоритма, на выходе мы получим непересекающиеся множетсва узлов, которые полностью покрывают полученное пространство разложения.
Возникает два вопроса: какую именно функцию выбрать в качестве стоимостной и каким образом этот алгоритм адаптировать к задаче классификации и кластеризации.
В примере, рассмотренном ниже, была использована функция 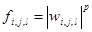 , где
, где 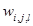 - это вейвлет-коэффициент, а
- это вейвлет-коэффициент, а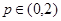 . Стоимостная функция всего узла, таким образом, будет равна
. Стоимостная функция всего узла, таким образом, будет равна 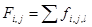 . Проведём вейвлет-преобразование входного сигнала X = {2, -10, 5, 0, 4, 16, 7, -2}. Дерево декомпозиции выглядит следующим образом:
. Проведём вейвлет-преобразование входного сигнала X = {2, -10, 5, 0, 4, 16, 7, -2}. Дерево декомпозиции выглядит следующим образом:
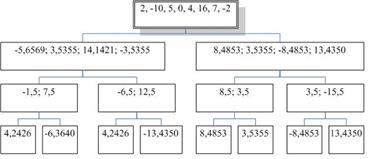
Используя предложенную характеристическую функцию, были отобраны узлы {(1,0), (2,2), (2,3)}.
Теперь обратимся к вопросу адаптации этого алгоритма к задачам классификации и кластеризации. В [7] было предложено в качестве стоимостной функции применить расстояние Кульбака-Лейблера. На самом деле, получая очередной образец, мы стремимся увеличить расстояние между классами, что позволит точнее соотнести входной сигнал с классом.
Итак, сначала зададим сигнал, принадлежащий классу А. Тогда энергию этого класса можно получить по формуле 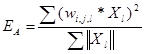 . А расстояние Кульбака-Лейблера мы вычислим по формуле
. А расстояние Кульбака-Лейблера мы вычислим по формуле 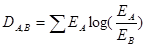 .
.
Теперь алгоритм будет выбирать базис, который увеличивает расстояние между классами, что повышает точность классификации. Но данное решение подходит не только для классификации. На самом деле, можно предположить, что входной сигнал будет единственным в своём классе. Тогда выбранный базис будет описывать расстояние между каждой парой входных сигналов. Такую матрицу расстояний уже можно будет обрабатывать стандартным методом, например, k-средних.
Литература:
1. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения // Успехи физических наук. 1996, том 166, №11. с. 1145-1170.
2. Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. ВУС, 1999.
3. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их использование // Успехи физических наук. 2001, том 171, №5. с. 465-501.
4. Стояновский С.Ю. Сжатие речевых сигналов с использованием ортогональных и биортогональных вейвлет-функций // Світ інформації та телекомунікацій - 2005. Матеріали ІІ міжнародної науково-технічної конференції студенства та молоді. Київ 2005, 174 с.
5. Шитов А.Б. Разработка численных методов и программ, связанных с применением вейвлет-анализа для моделирования и обработки экспериментальных данных // диссертация на соискание учёной степени кандидата физико-математических наук. Ивановский Государственный университет. Иваново, 2001.
6. Percival, Donald B. Wavelet methods for time series analysis / Donald B. Percival and Andrew T. Walden Cambridge University Press 2000.
7. Saito Naoki Local Feature Extraction and Its Application Using a Library of Bases // a Dissertation Present to the Faculty of the Graduate School of Yale University in Candidacy for the Degree of Doctor of Philosophy. 1994.
8. Thuillard, Mark Wavelets in Soft Computing. World Scientific Series in Robotics and Intelligent Systems – Vol. 25. World Scientific Publishing Co. Ptl. Ltd. 2001.
9. Urban, Karsten Wavelets in numerical simulation: problem adapted construction and application. Springer-Verlag Berlin Heidelberg 2002. (Lecture notes in computational science and engineering; Vol. 22).







