Если я видел дальше других,
то лишь потому, что стоял
на плечах гигантов.
/И. Ньютон/
Нужно ли излагать учащимся физику впоследовательности её исторического развития?
Механика – фундаментальный раздел физики. От усвоения этого раздела зависит усвоение смежных разделов физики.
Бытует мнение о том, что нет необходимости излагать учащимся физику в последовательности её исторического развития, с историческими экскурсами. Это, мол, излишние затраты времени, не вполне продуктивно и т. д.
Однако есть и противоположная точка зрения. Она отражена эпиграфом. В соответствии с ней ниже представлена методика изложения тем «Законы Кеплера», «Закон всемирного тяготения», «Кольцо Сатурна», «Первая космическая скорость для центрального тела», «Характер движения центрального тела. Двойные звёзды», «Закон сохранения момента импульса» с привлечением материала смежных теми исторических экскурсов.
Биографические сведения, приведённые в данной работе, заимствованы из работы [1].
Работа может быть полезна методистам, учителям физики, а также обучающимся физике.
II. Роль астрономии в создании основ механики
Нетрудно заметить, что все физики (и философы), причастные к формированию классической механики, были астрономами (и/или астрофизиками): Коперник (1473-1543), Галилей (1564-1642), Кеплер (1571-1630), Декарт (1596-1650), Ньютон (1643-1727).
Этого факта достаточно, чтобы утверждать, что астрономия сыграла важную роль в формировании основ механики.
Галилей, Кеплер и Декарт, несомненно, были в числе тех гигантов, на плечах которых стоял Ньютон.
Вот почему использование достижений этих учёных способствовало бы более глубокому усвоению механики в школе.
III. Достижения Галилея в физике (и астрономии)
«Движенья нет!», – сказал мудрец брадатый.
Другой вскочил и стал пред ним ходить.
Хвалили все ответ замысловатый.
/А. С. Пушкин/
Считается, что именно от выдающегося итальянского физика Галилео Галилея берёт начало физика как наука – наука теоретическая и экспериментальная. В пизанском университете он изучал медицину, но, увлёкшись геометрией и механикой в частности сочинениями Евклида и Архимеда, оставил университет и самостоятельно изучал математику [1].
Галилей изобрёл и изготовил телескоп (в 1609 г.) и, используя его, сделал ряд астрономических открытий:
установил наличие кольца у планеты Сатурн,
обнаружил четыре самых больших спутника у планеты Юпитер (Каллисто, Ио, Европа и Ганимед),
пришел к выводу о том, что Млечный путь – это множество звёзд, аналогичных Солнцу.
Галилей (как и Джордано Бруно) отстаивал гелиоцентрическую систему Николая Коперника.
После этих открытий Галилея вопрос о неподвижном центре мира вновь нуждался в исследовании. А есть ли он? Нужен ли он? Эти вопросы были поставлены Галилеем (такие же вопросы ставил и Джордано Бруно). Оба мыслителя отличались смелостью мышления.
Галилеем были установлены законы кинематики двух видов движения точки: равномерного и равнопеременного.
Исследуя кинематику тел, движущихся по наклонной плоскости, он пришёл к закону инерции (динамического характера): для поддержания равномерного прямолинейного движения сила (причина) не нужна. Более того, для прекращения движения требуется сила (в данном случае – сила трения).
Галилей выделил равномерное прямолинейное движение из иных видов движений (движений с ускорением) и пришёл к выводу о том, что такое движение сохраняется само по себе. Это было значительным достижением в механике. Здесь Галилей решился выступить против суждения древнегреческого философа Аристотеля. Аристотель полагал, что для любого движения нужна сила. Это суждение просуществовало как закон динамики около двух тысяч лет.
Закон инерции Галилея был также сформулирован позднее Декартом, а ещё позднее – Ньютоном. Он называется сейчас первым законом Ньютона. Галилеем был сформулирован принцип относительности движений.
Им была выявлена изохронность движений двух категорий:
падений тел различной массы на Землю с одной высоты,
колебаний (гравитационного) маятника.
IV. Кинематические законы Кеплера
Немецкий учёный Иоганн Кеплер (астроном, механик, математик и оптик) ученик и последователь датского астронома Тихо Браге, активный сторонник гелиоцентрической системы Коперника.
Исходя из эмпирических данных (данных наблюдений) о движении планет Солнечной системы, Кеплер установил три знаменитых закона.
Орбиты планет – эллипсы, в одном из фокусов которых находится Солнце
Примечание. Из первого закона Кеплера следует простое, но важное (для динамики) следствие:
Солнце и орбита планеты лежат в одной плоскости.
Структура «Солнце – планета» – плоская.
Радиус-вектор планеты в равные промежутки времени описывает равные площади
Промежутки времени здесь подразумеваются малыми по сравнению с периодом обращения планеты вокруг Солнца.
Этот закон можно выразить формулой:
rvsinα = const, (1)
где
r – расстояние от Солнца до его спутника (планеты) в произвольный момент времени,
v–модуль скорости спутника Солнца (планеты) в произвольный момент времени,
α – угол между векторами rи vв произвольный момент времени.
Квадраты периодов обращения (Т1и Т2) планет относятся как кубы больших полуосей (r1 и r2) их орбит
(Т1/ Т2)2 = (r1 / r2)3 (2)
Предлагается более простая для учащихся формулировка этого же закона:
средняя угловая скорость движения планеты по орбите и большая полуось орбиты связаны следующей формулой:
-
r3ω2 = constК
,(3)
ω = 2π/Т , (4)
где
ω– средняя угловая скорость движения планеты по орбите,
Т–период обращения планеты вокруг Солнца,
r –радиусокружности, описанной вокруг орбиты (эллиптической) – большая полуось орбиты,
constК– названа здесь постоянной Кеплера (для Солнца).
Нетрудно вычислить постоянную Кеплера для Солнца:
constК≈4 ·1014 м3 /с2 .
r3ω2– кинематический инвариант планет Солнечной системы, равный постоянной Кеплера (constК).
Примечание: Орбита и описанная вокруг неё окружность совпадают, если орбита круговая. В этом случае модули средней и мгновенной угловых скоростей совпадают. Среди планет солнечной системы только Меркурий и Плутон имеют орбиты с заметным отклонением от окружности. Далее речь идёт только о круговых орбитах.
Заметим, что законы Кеплера – кинематические: они не содержат массу планет (спутников Солнца). На первый взгляд это кажется невероятным. Неужели кинематика планет не зависит ни от массы планет, ни от массы центрального тела – Солнца? Ответы на оба вопроса будут получены ниже.
Если бы Кеплер свои законы смог рассмотреть с позиций динамики (сформированной позднее Ньютоном), то он мог бы предложить динамический закон, являющийся следствием законов Кеплера. Этот закон можно было бы назвать «четвёртый закон Кеплера».
Кинематика планет Солнечной системы не зависит от массы планет
В более общем виде этот закон имеет следующую формулировку.
Кинематика спутников центрального тела не зависит от их массы
Здесь подразумевается, что масса спутников во много раз меньше массы центрального тела.
Кеплером было предложено понятие силы как причины ускорения. Однако второй закон Ньютона – это достижение Ньютона.
V. От достижений Галилея, Кеплера и Декарта к законам Ньютона
Роль Ньютона в механике аналогична роли Евклида в геометрии. Евклид привёл в систему известные знания по геометрии, придав им аксиоматическую структуру. То же самое сделал Ньютон в механике. Благодаря ему, «необозримый массив данных о движении огромных небесных тел и мельчайших песчинок удалось свести к трём законам Ньютона и фундаментальному закону всемирного тяготения – так родилась первая научная картина мира» [2, с. 3]. Следует заметить, что все перечисленные законы Ньютона фундаментальны в том смысле, что они входят в аксиоматику классической механики.
Законы Кеплера сейчас можно вывести из следующих законов динамики и кинематики: закона всемирного тяготения, второго закона Ньютона и формулы центростремительного ускорения. Но во времена Кеплера основы классической динамики, включая закон всемирного тяготения Ньютона, не были открыты, и динамика ещё не оформилась в аксиоматическую структуру.
Рассмотрим, как мог бы рассуждать Ньютон, учитывая научные достижения Галилея, Кеплера и Декарта, открывая свой знаменитый закон всемирного тяготения.
Наличие спутников у Земли (Луна), у Юпитера (множество), а также кольца у Сатурна наводит на мысль об особой важности кругового равномерного движения,по крайней мере, в Солнечной системе. Такое движение может носить всемирный характер.
Для поддержания равномерного прямолинейного движения сила не нужна (Галилей). Для осуществления остальных видов движений (по отношению к ним суждения Аристотеля справедливы) необходима сила, которая определяется формулой (второй закон Ньютона):
f = ma . (5)
В частности, для движения по окружности необходима сила, называемая центростремительной (Ньютон):
f = mv2 / r . (6)
Этой силе (f) соответствует центростремительное ускорение (а) согласно второму закону Ньютона (5):
a = v2 / r = rω2 . (7)
Следовательно, между парой небесных тел (центральное тело – спутник) должны действовать силы притяжения (гравитационные силы), равные указанной центростремительной силе.
Отразим эту мысль на рисунке 1.
Пусть имеется пара небесных тел массами m и m.
Здесь и далее размер символа имеет значение.
Определение 1. Более массивное тело в паре называются центральным телом.
Определение 2. Менее массивное тело в паре называются спутником (центрального тела).
Определение 3. Совокупность центрального тела и его спутника (спутников) называется спутниковой структурой.
При этом будем подразумевать справедливость следующего неравенства:
m << m . (8)
Рис. 1. Гравитационное взаимодействие пары тел
m – масса центрального тела,
m – масса спутника,
f –сила, действующая на спутник, со стороны центрального тела,
f – сила, действующая на центральное тело со стороны спутника,
r – расстояние между телами,
ω – угловая скорость движения спутника по круговой орбите.
Попытаемся выявить формулу, отражающую зависимость действующей между парой тел силы тяготения от других физических величин.
Перечислим физические величины (параметры), от которых может зависеть эта сила, а также сделаем некоторые предположения о характере качественной зависимости силы тяготения от этих величин.
Предположим, что эта сила не зависит от скорости движения тел. Так, если тела неподвижны, то между ними действует та же сила.
Ньютон понимал, что пара тел может взаимодействовать друг с другом только с силами – антиподами – лежащими на одной прямой, противоположно направленными и равными по модулю. Это свойство взаимодействия пары тел не зависит от природы сил и носит всеобщий характер.
Такое понимание сил – антиподов, возникающих при взаимодействии тел пары, нашло отражение в третьем законе Ньютона:
f = - f.(9)
Модули этих сил равны:
f = f.(10)
Логично предположить, что эти силы – антиподы зависят от масс каждого из тел пары.
В противном случае пара могла бы изменять характер движения своего центра масс за счёт внутренних сил. Это было бы невероятным явлением, противоречащим экспериментальным данным. Т.е. в этом случае не может быть выполнен закон сохранения импульса пары тел, который (для случая взаимодействия и движения тел вдоль прямой линии) был известен ещё Декарту:
mv = - mv . (11)
Если тела пары были неподвижны до взаимодействия, то после взаимодействия их импульсы в сумме равны нулю – см. (11).
Из формулы (11) следует, что центр масс пары после взаимодействия так же остаётся неподвижным, как и до взаимодействия. Это – ещё одна формулировка закона сохранения импульса.
Понятно, что в искомую нами формулу массы должны входить симметрично в силу равноправия тел пары.
Логично предположить также положительную корреляцию силы тяготения и масс тел пары. Т.е. чем больше массы тел, тем больше сила тяготения.
Логично предположить также отрицательную корреляцию между силой тяготения и расстоянием (r) между телами. Т.е. чем больше расстояние между телами, тем меньше сила тяготения.
Предположим, что искомая формула имеет вид степенной функции, в которой показатели степеней (х и у) подлежат выявлению – см. (12).
С учётом указанных предположений формула закона тяготения пары тел может иметь вид
-
f= f= γ(mm)х / rу
(12)
или иной вид
-
f= f =γ(m+m)z/ rу,
(13)
где
γ– неизвестная постоянная, необходимая для уравнивания размерностей и числовых значений обеих частей выражений (12) и (13), получившая название «гравитационная постоянная».
Возможны и иные варианты искомой формулы, они здесь не представлены.
Покажем, что при х = 1 формула (12) удовлетворяет экспериментальным данным Галилея – изохронности падения тел (различной массой) на Землю с одинаковой высоты, а также четвёртому закону Кеплера.
Действительно, при х = 1 формула (12) принимает вид
-
f= f= γmm / rу.
(14)
Тогда, согласно второму закону Ньютона (5), центростремительное ускорение (а) спутника (массой m)примет вид
|
v2 / r = a = f / m = γm / rу , |
(15) |
где
v– скорость спутника на круговой орбите радиусом (r).
Как видим, формула (15) центростремительного ускорения спутника не содержит его массу (m).
Разделим выражение (15) на радиус орбиты (r), получим
-
a / r= v2 / r2= ω2 = γm/ rуr.
(16)
Из (16) получим
-
rуrω2 = γm= const .
(17)
Сравнивая выражение (17) с формулой (3) третьего закона Кеплера, можно заметить, что при у=2 обе формулы совпадают, при этом постоянная величина (const) в (17) является постоянной Кеплера (constК). Следовательно, числовое значение второго показателя степени выражения (12) равно двум:
у = 2 . (18)
Учитывая (18), из (14) получим искомый закон гравитационного взаимодействия пары тел, или закон всемирного тяготенияНьютона:
-
f= f= γmm / r2 . (19)
Очевидно, что этот закон, полученный путём рассуждений (возможно, так рассуждал Ньютон) и опоры на первичные (в историческом плане) законы Кеплера, выявленные из анализа экспериментальных данных, производит большее впечатление на учащихся, чем этот же закон, представленный учащимся фразой учителя: «Запомните дети, что…». В современных школьных учебниках этот закон излагается так, будто он упал с неба как яблоко с яблони на голову Ньютона в дошедших до нас рассказах народных историков физики. Как мы убедились, этот закон можно назвать упавшим с неба лишь в том смысле, что истоки закона находятся в астрономических законах Кеплера.
Учитывая (18), (17) примет вид:
-
r3ω2 = γm = constК .
(20)
Получен закон, который назовём обобщённым третьим законом Кеплера(20).
Этот закон имеет уже кинематико-динамический характер и является более содержательным, чем третий закон Кеплера, поскольку в нём раскрыт физический смысл постоянной Кеплера в правой части третьего закона Кеплера (3).
Постоянная Кеплера (constК) есть произведение массы центрального тела (m) и гравитационной постоянной (γ). Закон (20) позволяет по кинематике кругового движения спутников вычислять массу центрального тела (m) – динамическую величину. Т.е. из одних лишь наблюдений за спутником любого небесного (центрального) тела, можно установить массу этого тела. Закон (20) даёт ответ на поставленные выше вопросы о влиянии масс на кинематику спутника.
Английский физик Максвелл предлагал гравитационную постоянную γ принять за безразмерную единицу и считать размерность массы равной кубу размерности длины, делённому на квадрат размерности времени. В этом случае масса считалась бы кинематической величиной.
Необходимо заметить, что три закона Ньютона (первый, второй и третий) можно было бы открыть эмпирически в лаборатории, оборудованной необходимыми приборами. В то же время закон всемирного тяготения без третьего закона Кеплера и без изохронности падения на Землю тел разной массы (а также без соответствующих рассуждений) открыть в лаборатории было бы труднее.
Числовое значение гравитационной постоянной было экспериментально выявлено Кавендишем в лаборатории в 1798 году, с использованием двух пар притягивающихся тел и крутильных весов. Таким образом, английский физик Кавендиш «взвесил» Землю.
В пределах Солнечной системы мы наблюдаем спутниковые системы планет, кинематика которых соответствует законам Кеплера. Два спутника Марса –пример такого соответствия – см. раздел XII.
С учётом того, что кинематика спутников планет Солнечной системы также вписывается в законы Кеплера, можно предположить, что эти же законы работают во всей Вселенной. Это означает, что и законы Ньютона (второй, третий и всемирного тяготения) также работают во всей Вселенной.
С учётом этого предположения из обобщённого третьего закона Кеплера (20) следует, что Кавендиш «взвесил» центральное тело любой видимой спутниковой структуры. Теоретический фундамент этого «взвешивания» был заложен Галилеем, Кеплером и Ньютоном.
VI. Некоторые следствия обобщённого третьего закона Кеплера
Подставляя (18) в (15), получим формулу центростремительного ускорения (а) спутника на орбите (r):
-
a = v2 / r = γm / r2 .
(21)
Подставляя (18) в (16), получим формулу квадрата угловой скорости (ω2) спутника на орбите (r):
a / r = v2 / r2= ω2 = γm/r3. (22)
Из (22) получим формулу угловой скорости (ω) движения спутника по круговой орбите:
-
ω = (γm / r3)0,5 .
(23)
Умножив числитель и знаменатель подкоренного выражения формулы (23) на 4π/3, ей можно придать следующий вид:
-
ω = Е (γρ)0,5 ,
(24)
V = 4πr3 / 3 , (26)
-
Е = 2 (π / 3)0,5 ≈ 2,05 ,
(27)
где
V – объём шара радиусом, равным радиусу орбиты,
Е – безразмерная постоянная величина,
![]() – орбитальная
плотность центрального тела (для круговой орбиты с радиусом r).
– орбитальная
плотность центрального тела (для круговой орбиты с радиусом r).
Определение 4. Отношение массы планеты к объёму шара, имеющего радиус круговой орбиты спутника, назовём «орбитальной плотностью планеты».
Заметим, что формула (24) проще формулы (23). Формула (24) показывает, что единственным параметром, определяющим угловую скорость спутника на данной орбите (r), является «орбитальная плотность планеты»(ρ).Эта плотность определяется массой центрального тела (m) и радиусом (r) орбиты спутника – см. (25 и 26).
Из (21) получим две формулы для орбитальной скорости спутника:
v = (а r)0,5 , (28)
v = (γm / r)0,5.(29)
Заметим, что формула (29) получается также из следующей формулы
v = ω r(30)
с учётом формулы (23).
Учитывая (30), получим ещё две формы обобщённого третьего закона Кеплера-Ньютона (20), справедливые для круговых орбит спутников центрального тела:
|
rv2= γm = constК, |
(20.1) |
|
v3/ ω = γm = constК. |
(20.2) |
Выражения rv2 и v3/ω это ещё два кинематических инварианта (наряду с инвариантом r3ω2= constК) спутников на круговых орбитах центрального тела.
VII. Как движутся спутники Сатурна, образующие его кольцо?
Если посмотреть в телескоп на планету Сатурн, то можно увидеть необычную структуру. Кажется, что на планету надето кольцо, похожее на шайбу.
Первым это увидел Галилей, вооружившись своим телескопом, в 1609 году.
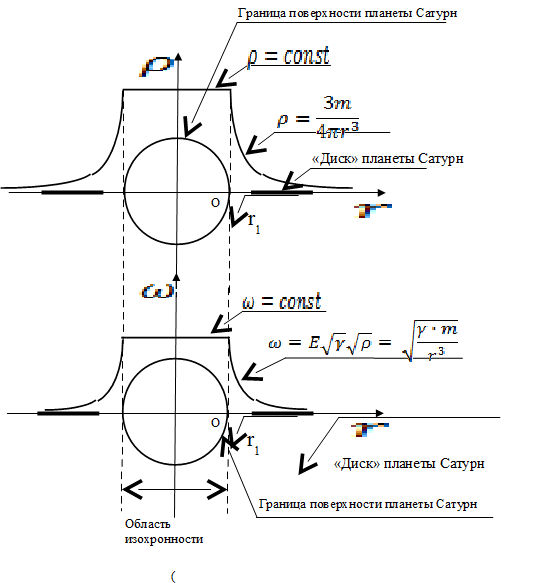
Формулы (23 и 24) отражают свойство кольца Сатурна (это свойство спутников, имеющих круговые орбиты, входящих в спутниковую структуру): угловые скорости орбитального движения спутников на разных круговых орбитах не являются одинаковыми. Спутники каждой круговой орбиты движутся со своей угловой скоростью, которая убывает как квадратный корень из орбитальной плотности. Формулу (24) можно записать, выделив в ней постоянную величину (соnst):
|
(31) |
соnst = (constКС)0,5 =(γm)0,5 , (32)
где
constКС= γm – константа Кеплера для Сатурна,
m – масса Сатурна.
Из формулы (31) следует, что угловая скорость движения спутника центрального тела на круговой орбите убывает как корень полуторной степени из радиуса круговой орбиты.
Формула (24)
отражает также следующее суждение: циклическое
движение тела (массой m)
в диаметральном сквозном туннеле однородного (![]() )
центрального тела (массой m)
имеет постоянную циклическую (круговую) частоту (ω) такого
движения. Это означает, что такие движения изохронны.
)
центрального тела (массой m)
имеет постоянную циклическую (круговую) частоту (ω) такого
движения. Это означает, что такие движения изохронны.
Графики зависимостей орбитальной плотности () и угловой скорости (ω) обращения спутников Сатурна, входящих в состав кольца, от расстояния (r) от центра Сатурна представлен на рисунке 2.
Рис. 2. Зависимость угловой скорости обращения спутников Сатурна, входящих в состав кольца, от расстояния до его центра
Спутниковая структура «планета Сатурн – спутники, образующие кольцо Сатурна» является плоской. Если бы мы, находясь на одном из тел кольца Сатурна, посмотрели вокруг, то увидели бы на небе сплошную полосу, пересекающую небо, аналогичную Млечному Пути. Эта полоса казалась бы нам «Луной» в виде полосы, разделяющей небосвод на две части.
В свою очередь, полоса Млечного Пути также представляет собой близкую к плоской спутниковую структуру – нашу Галактику, спутниками которой служат звёзды нашей Галактики. Солнце лежит в плоскости этой спутниковой структуры.
Спутниковая структура «Солнце и планеты» также является плоской: орбиты планет лежат в одной плоскости.
VIII. Первая космическая скорость для центрального тела
Определение 5. Первой космической скоростью (vI) для центрального тела называется орбитальная скорость спутника при радиусе орбиты, равном радиусу (r1) центрального тела.
Если в формулах, содержащих расстояние (r) между парой тел, положить это расстояние равным радиусу (r1) центрального тела
r = r1 , (33)
то получим кинематические характеристики спутника на минимально возможнойкруговой орбите. Подставляя (33) в (22), получим формулу ускорения свободного падения:
|
a1 = g1= vI2 / r1 = γm/(r1)2 . |
(34) |
Учитывая (33), из (28) и (29) следует формула первой космической скорости (vI):
vI =(γm / r1)0,5= (g1r1)0,5 . (35)
Обычно индекс «1» у ускорения свободного падения (g1)опускают:
vI = (γm/ r1)0,5 = (gr1)0,5 . (36)
Подставляя в (36) числовые значения g и r1
g= 10 м/с2 ,
r1= 6 400 000 м ,
получим
vI = 8 000 м/с .
Из формулы (24) следует, что для любого центрального тела максимальная угловая скорость (ω) орбитального движения спутника, движущегося по круговой орбите, это угловая скорость (ω1) спутника, движущегося по круговой орбите радиусом r1(с первой космической скоростью). Это отражено также на рис.2.
ω1 = vI/r1 – угловая скорость кругового орбитального движения спутника, движущегося с первой космической скоростью.
Из формулы (29) следует, чтодля любого центрального тела первая космическая скорость это максимальная скорость спутника, движущегося по круговой орбите.
IX. Характер движения центрального тела. Двойные звёзды
Строго говоря, в силу равноправия тел пары центральное тело также совершает движение по круговой орбите радиусом (rц), гораздо меньшем расстояниямежду телами (r):
rц<<r. (37)
Докажем справедливость неравенства (37).
Обозначим расстояния от тел пары до их центров масс так:
rц – расстояние от спутника до центра масс пары,
rц – расстояние от геометрического центра центрального тела до центра масс пары.
Положение центра масс определяется по известной формуле «рычага Архимеда»:
mrц = mrц. (38)
Из (38) следует:
rц/ rц = m / m<< 1 . (39)
r = rц + rц . (40)
Из (39) и (40) следует
rц<<rц , (41)
или
rц<<rц + rц = r, (42)
что и требовалось доказать.
Пара совершает вращение вокруг общего центра масс с одинаковой круговой частотой (ω). Ввиду принятого нами условия (8) центр масс пары практически совпадает с центром масс центрального тела, потому можно считать, что движение спутника происходит относительно центра масс центрального тела.
Существуют так называемые двойные звёздные структуры (двойные звёзды) – пары звёзд с соизмеримыми массами. Такая пара совершает вращательное движение. Центром вращения служит центр масс двойной звёздной структуры. В таких структурах условие (8) снимается, но принцип расчёта механических характеристик таких структур не отличается от рассмотренного выше.
Для двойной звёздной структуры с равными массами можно применять формулы (24-27). При этом в формуле (25) буква m означает суммарную массу двух звёзд, а в формуле (26) буква r означает радиус круговой орбиты каждого из тел (звёзд) двойной звёздной структуры.
Установлено, что двойныхзвёздных структур в обозримой части Вселенной больше, чем одиночных звёзд.
Х. Закон сохранения момента импульса
Согласно второму закону Кеплера при гравитационном взаимодействии пары сохраняется следующая величина, отражающая геометро-кинематическую характеристику спутника:
rvsinα = const . (43)
В силу равноправия тел пары сохраняется величина, аналогичная левой части выражения (43), относящаяся ко второму телу пары (к центральному телу) для того же момента времени:
rvsinα = const. (44)
Выражения (43) и (44) являются геометро-кинематическими. Выражение (43) не содержит массу спутника (m). Причина этого выявлена выше: движения спутников по любым траекториям не зависят от массы спутников. Это – экспериментальный результат, полученный Галилеем и Кеплером и объяснённый Ньютоном.
По этой же причине выражение (44) не содержит массу центрального тела (m).
Умножим обе части каждого из выражений (43) и (44) на соответствующую массу, получим
mr v sinα = const · m = const1,(45)
m r v sinα = const · m = const1 . (46)
Сложим почленно выражения (45) и (46), получим
mrvsinα + mrvsinα = const1 + const1 = CONST . (47)
или
m r v sinα + m r v sinα = CONST . (48)
Выражение (48) – символьная форма закона сохранения «момента импульса» пары тел при гравитационном взаимодействии этих тел.
В данном случае нет нужды использовать векторную форму этого закона в силу отмеченного выше следствия первого закона Кеплера: движение тел пары – плоское.
Выражения, содержащие угол (α), упрощаются для двух положений планеты на орбите вокруг Солнца: афелия и перигелия. В этих точках орбиты угол (α) равен 90°. Тогда sinα = sin90°=1.
При круговых орбитах формула (48) упрощается и принимает вид:
m r v + m r v = CONST . (49)
Впоследствии (в 1746г.) физиками (Л. Эйлером и Д. Бернулли) было установлено, что закон сохранения момента импульса пары тел справедлив при любом механическом взаимодействии тел пары (а не только гравитационном). Условием выполнения этого закона является замкнутость пары, т. е. отсутствие внешних сил (и моментов сил), действующих на пару.
Векторная форма закона сохранения момента импульса пары тел при любом механическом взаимодействии тел пары с использованием понятия «векторного произведения векторов» имеет вид:
mr×v + mr×v = CONST . (50)
В программе средней школы (базовый уровень) нет темы «закон сохранения момента импульса», несмотря на то, что этот закон входит в число фундаментальных законов механики, имеет прикладное значение в современной технике, а кинематическая форма этого закона (для пары тел, взаимодействующих гравитационными силами) представляет собой второй закон Кеплера (XVII в.). Кроме того, изучение этого закона необходимо и потому, что он используется в разделах «Квантовая теорияэлектромагнитного излучения и вещества», «Физика атомного ядра» и «Элементарные частицы».
Заметим, что закон (48) получен нами (из второго закона Кеплера) дедуктивным методом для гравитационных взаимодействий. Обобщение его на любые другие взаимодействия – это уже индукция – экстраполяция, требующая экспериментального обоснования. Имеющиеся экспериментальные данные не противоречат этому закону.
ХI. Итоговые формулы
Полученные итоговые формулы сведём в таблицу «Итоговые формулы».
Итоговые формулы
|
№ п/п |
Формула |
Наименование формулы |
Автор |
|
|
r3ω2 = const |
Третий закон Кеплера |
Кеплер |
|
|
r3ω2 = γm = constК |
Обобщённый третий закон Кеплера для круговой орбиты (первая форма) |
Получена из формул Кеплера и Ньютона |
|
|
rv2 = γm = constК |
Обобщённый третий закон Кеплера для круговой орбиты (вторая форма) |
Получена из формул Кеплера-Ньютона |
|
|
v3/ω = γm = constК |
Обобщённый третий закон Кеплера для круговой орбиты (третья форма) |
Получена из формул Кеплера-Ньютона |
|
|
f = ma |
2-ой закон Ньютона |
Ньютон |
|
|
f= - f |
Третий законНьютона |
Ньютон |
|
|
f= mv2 / r |
Сила центростремительная |
Ньютон |
|
|
a = v2 / r |
Ускорение центростремительное |
Ньютон |
|
|
f= γmm / r2 |
Закон всемирного тяготения |
Ньютон |
|
|
ω = (γm / r3)0,5 |
Угловая скорость движения спутника по круговой орбите |
Получена из формул Кеплера-Ньютона |
|
|
V = 4πr3 / 3 Е = 2 (π / 3)0,5 ≈ 2,05 |
Угловая скорость движения спутника по круговой орбите Орбитальная плотность планеты Объём шара радиусом, равным радиусу орбиты Безразмерная постоянная величина |
Получены из формул Кеплера-Ньютона
|
|
|
v = (а r)0,5 |
Орбитальная скорость спутника |
Ньютон |
|
|
v = (γm/ r)0,5 |
Орбитальная скорость спутника |
Ньютон |
|
|
a = γm/ r2 |
Центростремительное ускорение |
Ньютон |
|
|
vI = (gr1)0,5 |
Первая космическая скорость центрального тела |
Ньютон |
|
|
vI = (γm / r1)0,5 |
Первая космическая скорость центрального тела |
Ньютон |
|
|
a1=g1= γm/ (r1)2 |
Ускорение свободного падения на поверхности центрального тела |
Ньютон |
|
|
r v sinα = const |
Второй закон Кеплера для спутника |
Кеплер |
|
|
rvsinα = const |
Второй закон Кеплера для центрального тела |
Кеплер, Ньютон |
|
|
m r v sinα + mrv sinα = CONST |
Закон сохранения момента импульса пары тел
|
Л. Эйлер и Д. Бернулли(1746) |
|
|
mr × v + mr × v = CONST |
Закон сохранения момента импульса пары тел |
Л. Эйлер и Д. Бернулли(1746) |
ХII. Рассуждения Лемюэля Гулливера о третьем законе Кеплера
Наличия геометро-кинематических данных орбит двух спутников достаточно для того, чтобы выявить справедливость (или несправедливость) третьего закона Кеплера по отношению к кинематике этих спутников.
Ниже приведён (близкий к оригинальному тексту) фрагмент из книги Дж. Свифта [3], иллюстрирующий эту мысль, использованный в работе [4, с. 66].
«Они открыли две маленькие звезды или спутники, обращающихся около Марса, из который первый удалён от центра этой планеты на расстояние, равное трём (3) её диаметрам, а другой – на расстоянии пяти (5) таких же диаметров. Первый совершает своё обращение в течение 10 часов, а второй в течение 21 с половиной часа, так что квадраты времён их обращения почти пропорциональны кубам их расстояния от центра Марса, каковое обстоятельство с очевидностью показывает, что означенные спутники управляются тем же самым законом тяготения, которому подчинены другие небесные тела…».
Джонатан Свифт – известный английский писатель-сатирик младший современник Ньютона, получивший степень магистра в Оксфорде, а позднее степень доктора богословия в Тринити-колледже. Вкладывал ли писатель в это суждение что-либо сатирическое – нам неведомо, но ясно одно: он прекрасно разбирался в проблемах астрономии (и астрофизики) того времени, и его суждения корректны. Действительно,
()3 = 4,629 ,
(2 = 4,622 .
Если бы у Марса был один спутник, то показать, что спутник Марса «управляется тем же самым законом тяготения (третьим законом Кеплера), которому подчинены другие небесные тела» было бы невозможно без формул динамики Ньютона и закона всемирного тяготения, которые появились позднее, благодаря третьему закону Кеплера.
Если, к тому же, у всех планет солнечной системы был бы только один спутник, то открытие третьего закона Кеплера было бы также невозможно по данным наблюдений за спутниками планет солнечной системы (без формул динамики Ньютона).
Если бы у Солнца был бы единственный спутник – Земля, то открытие третьего закона Кеплера, исходя из наблюдений за единственным спутником, было бы невозможно (без формул динамики Ньютона). Это затормозило бы развитие физики.
Как планет, так и спутников этих планет хватило для открытия кинематических законов Кеплера.
Движение спутников планет по тем же законам, что и спутников Солнца (планет) дало основание выдвинуть гипотезу о том, что третий закон Кеплера является вселенским законом и назвать закон всемирного тяготения Ньютона всемирным (вселенским).
Эмпирический материал в достаточном объёме – мощный стимул для развития физики.
Примечания:
В процитированном фрагменте книги Свифта «тот же самый закон тяготения» – это динамическая трактовка третьего закона Кеплера.
Это кажется невероятным, но оба спутника Марса были открыты лишь в XIX веке (в 1877 г., Астаф Холл, США). Они получили названия Фобос и Деймос.
Периоды их обращения вокруг Марса таковы:
Фобос – 8 ч. 12 мин., Деймос – 30 ч. 17 мин.
Оба спутника – крошечные. Максимальный размер
Фобоса – 28 км, аДеймоса –16 км.
Фобос и Деймос на латыни означают Страх и Ужас (они, согласно мифологии, – внуки Марса).
XIII. ЗАКЛЮЧЕНИЕ
Предложенная методика изложения важнейших тем классической механики иллюстрирует межпредметную связь между физикой и астрономией (астрофизикой), а также связь между смежными темами физики.
С привлечением достижений Галилея, Кеплера и Декарта при изложении динамики Ньютона приводит к более глубокому усвоению материала. Демонстрация исторической последовательности развития классической механики в данном случае продуктивна.
Литература:
Храмов Ю. А. Физики: Биографический справочник. – М. Наука, 1983. – 399 с.
Садовничий В. А. О физике и биологии и их преподавании в школе. Выступление на Всероссийском съезде учителей физики и биологии в МГУ. – М.: МГУ, 2011. – 24 с.
Джонатан Свифт. Путешествия в некоторые отдалённые части света Лемюэля Гулливера, сначала хирурга, а потом капитана нескольких кораблей. – М.: Детская литература, 1980. – 200 с.
Фейгин О. О. Поразительная Вселенная. – М.: Эксмо, 2011. – 288 с.