Современные задачи, связанные с вычислительной физикой, характеризуются сложной геометрией, большим объемом вычислительной работы, связанной, прежде всего с её многомерностью. Организация и управление вычислительными процессами в этих условиях требуют наглядного представления информации - визуализации, позволяющей принимать решения о детализации вычислений данных в тех или иных областях параметров. Типичным примером тому служат задачи макроэкономики и эконофизики.
Визуализация является существенной частью процесса численного моделирования, обеспечивающей анализ и правильную интерпретацию результатов вычислений, а также дальнейшую работу с вычислительной моделью. Можно выделить три основных аспекта в проектировании и разработке систем компьютерной визуализации. Прежде всего, это проблематика, связанная с созданием, хранением, обработкой и выводом изображений с помощью ЭВМ, то есть непосредственно с машинной (компьютерной) графикой. Второй аспект касается проблем инженерии программного обеспечения, общих для многих приложений. Наконец, третий аспект связан с проблемами, относящимися к восприятию и интерпретации визуальных образов пользователем системы. [1]
В последнее десятилетие физики разных стран пытаются применить наработанные ими методики к анализу экономических процессов. Среди представителей этого направления появились уже Нобелевские лауреаты, но границы и области применения эконофизики все еще остаются спорным вопросом.
Системы, устроенные совершенно различно на микроуровне, на макроуровне, порой, ведут себя совершенно одинаково. Такие феномены успешно анализируются с помощью математического аппарата современной теоретической физики. Примерно десять лет тому назад физики попробовали использовать свои математические инструменты к анализу экономических явлений. Появился термин «эконофизика». [2]
Сегодня эконофизики решают только частные задачи, связанные с функционированием рынков. По мере развития этой науки, их инструментарий становится богаче, поэтому шансов решить очередную новую задачу у них становится больше.
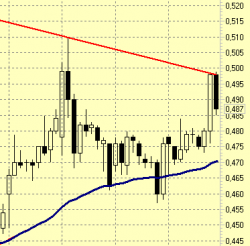
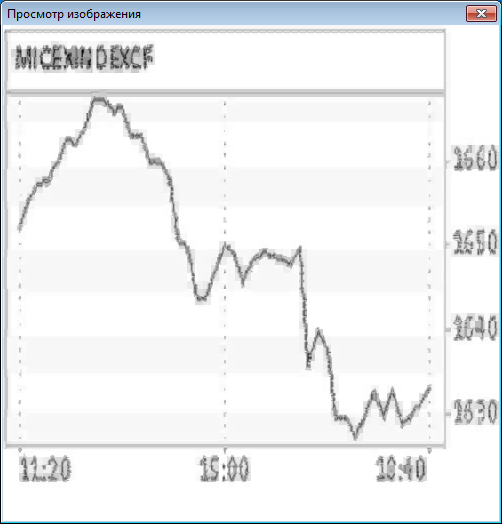
Ученые нашли способ извлекать прибыль при управлении активами с помощью фрактального анализа. Об этом заявил вице-президент УК "Интраст" Николай Старченко на первом Всероссийском конгрессе по эконофизике. По его словам, эксперты научились определять тип поведения инвестора в текущий момент времени на фондовом рынке. Как известно, это либо классическое блуждание (инвесторы действуют независимо), либо тренд (направленное движение цены), либо флэт (небольшие колебания вокруг равновесной цены). Эксперты пытаются использовать достижения эконофизики не только на фондовом и финансовом рынке, но и в макроэкономических прогнозах. Сегодня в Институте прикладной математики РАН начата работа над программой по математическому моделированию и системному анализу мировой динамики.[3]
Рис.1 фрактальный анализ графика цен акций на фондовом рынке
Экономика относится к разряду так называемых сложных самоорганизующихся систем, подобных биологическим. Но если медицина и биология в своих исследованиях могут формировать некие контрольные и экспериментальные группы, подвергая последних неким воздействиям, то в экономике экспериментальных площадок создать практически невозможно. Эконофизика двигается в исследовании следующим путем: некоторое явление, просматривающееся в статистических данных, позволяет сформулировать гипотезу, из которой всякий раз вытекает масса следствий. Их реализацию можно проверять уже опытным путем.
Тест истинности результата в физике – это его повторяемость в опытах разных исследователей. В микроэконофизике повторяемость тоже есть. Разные исследователи, решая одинаковую задачу, нередко приходят к близким результатам. Полного повторения, как в физике, в экономике, как и в биологии, и медицине, не бывает, это как раз и подразумевается в определении этих систем, как сложных.
В центре многих исследований физических систем, таких как, прогнозирование финансовых рынков и рынков ценных бумаг, системный анализ, сжатие изображения и жидкостная динамика, наука хаоса обещает продолжать производить поглощающую научную информацию, которая может сформировать лицо науки в будущем.[4]
Теория хаоса полезна как средство интерпретации научных данных в новом свете. Вместо традиционного графика X-Y, ученые могут теперь интерпретировать диаграммы фазового пространства, которые скорее являются описанием точного положения некоторой переменной относительно времени, и представляют полное поведение системы. Вместо поиска строгих формул, удовлетворяющие статистическим данным, мы можем теперь искать динамические системы с поведением подобным по природе статистическим данным, то есть системы, которые схожи с аттракторами.
Фактически любая хаотическая система может быть легко смоделирована — рынок акций обеспечивает тенденции, которые могут быть проанализированы с использованием "странного аттрактора" намного легче, чем с применением стандартных явных уравнений. Прикладные программные средства для обработки цифровых изображений
В настоящее время визуализация всей динамики движения экономических систем затруднена постоянно растущим объемом информации, что приводит в свою очередь к определенным потерям как во времени, так и в качестве анализа данных систем. Решение данной проблемы было найдено в применении кодирования и сжатия цифровых графических данных с целью уменьшения объема обрабатываемой информации. Программное вейвлет - преобразование данных
Вейвлет-анализ является в настоящее время одним из наиболее эффективных инструментов, предназначенных для исследования локальных пространственных и частотных характеристик сигналов [5,6]. В настоящей работе для решения задач локального вейвлет-анализа данных предполагается применение дискретного вейвлет-преобразования одномерного сигнала на примере вейвлет-базиса Хаара и быстрый алгоритм дискретного ортогонального вейвлет-разложения С.Малла [6]. Замена конструкции предполагает ее трансформацию от иерархической схемы вычислений, используемой в известных алгоритмах, к схеме, в которой вычисление коэффициентов для вейвлетов каждого уровня производится последовательно для всех его позиций на цифровом сигнале в рекурсивном режиме [7-9].
Данное изменение вычислительной конструкции вейвлет-преобразования позволяет отойти от «блочного» характера вычислений [5,6], который обычно приводит либо к избыточной в вычислительном плане схемы последовательного вычисления вейвлет-преобразования (для сильно перекрывающихся блоков анализа), либо к снижению качественных показателей анализа (при расположении блоков вейвлет-преобразования без перекрытий). Изменение вычислительной конструкции в параллельную или параллельно-рекурсивную форму, которая хорошо приспособлена к задаче локального «скользящего» анализа цифровых сигналов и изображений [7-9], приводит, в частности, к существенному снижению сложности обработки. Программное фрактальное кодирование данных
Одна из серьезных проблем машинной графики заключается в том, что до сих пор не найден адекватный критерий оценки потерь качества изображения. А теряется оно постоянно — при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати, и, что для нас особенно важно, при архивации с потерями.[10]
Проанализировав типы данных, которые участвовали в экспериментах, автором были найдены новые области применения алгоритмов сжатия данных со значительными потерями, а также с длительным временем обработки.
Анализ графиков движения акций на фондовых рынках актуально проводить очень продолжительное время, как говорят аналитики – «всегда», и поэтому объем графического материала будет со временем возрастать. Вот здесь и придет на помощь фрактальное кодирование данных, обладая хорошими показателями сжатия информации, несмотря на образующиеся артефакты на изображениях, а также длительную обработку данных.
Рис. 2 Фрактальное кодирование
Дело тут обстоит в следующем: проводя технический анализ на графиках с большим диапазоном по времени (в отличие от краткосрочных графиков), необходимость в минимизации времени сжатия данных уменьшается, так как в основном работа с большими интервалами по времени ведется в режиме оффлайн. Также появившиеся артефакты на изображении незначительно влияют на дальнейшую работу: основная линия графика прослеживается довольно четко и поддается обработке, фон же в свою очередь значения не имеет.
Для увеличения эффективности сжатия изображений были применены принципиально новые методы сжатия, допускающие некоторые потери информации, согласованные со зрительной системой человека.
Применение таких методов позволило достигать существенных значений коэффициентов сжатия. Такие методы принято относить к классу методов сжатия «с потерями».
Однако, в ряде областей техники применение современных методов компрессии изображений «с потерями» оказалось сильно ограничено, а в некоторых случаях и неприемлемо, что связано с недопустимым уровнем вносимых при кодировании ошибок, либо с эффектом визуализации ошибок, например, в результате их накопления в процессе цифровой обработки. К таким областям относятся те, в которых изображения подвергаются многократным обработкам, например, в издательском деле, в области цифровой видеосъемки при дальнейшем применении нелинейного видеомонтажа и т.п. А также, те области техники, в которых результирующие изображения выводятся на носители с растром, структура которого пространственно согласована со структурой растра принятого при сжатии (например, в полиграфии). Такое пространственное согласование приводит к проявлению (визуализации) ошибок преобразования при наложении растров. В то же время, в перечисленных областях, предъявляются весьма высокие требования к визуальному качеству результирующих изображений.
Таким образом, методы кодирования и сжатия на основе вейвлет и фрактального преобразования становятся все более популярными в области обработки данных, потому и были выбраны в качестве ключевых элементов в создании прикладных программных средств, используемых при проведении различных исследований на кафедре Прикладной Математики в Учебном Научном Институте Кибернетики и Технологий «УНИКИТ» Сургутского Государственного Университета «СурГУ».
Разработка средств компьютерной визуализации для научных исследований В.Л. Авербух ИММ УрО РАН, УрГУ г. Екатеринбург
А. Осетров: Что может и чего не может эконофизика, 2005
http://chaos.in.ua/news/poviedieniie-inviestorov-i-fraktal-nyi-analiz
Малинецкий Г. Г. Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. 3-е изд. М.: УРСС, 2001
Daubechies Ten Lectures on Wavelets // CBMS-NSF Lecture Notes nr. 61, SIAM, 1992.
S. Mallat A wavelet tour of signal processing // Aca- demic Press, 1999.
A.V. Chernov Fast Method for Local Image Processing and Analysis // A.V. Chernov, V.V. Myasnikov, V.V. Sergeyev Pattern Recognition and Image Analysis, Vol.9, No.4, 1999.
V.V. Myasnikov Methods for Designing Recursive FIR Filters // Proceedings of International Confer- ence “Computer Vision and Graphics” (ICCVG 2004), Warsaw, Poland, September 22-24, 2004, Springer.
Копенков В.Н., Быстрые алгоритмы локального дискретного вейвлет-преобразования с базисом Хаара. Копенков В.Н., Мясников В.В НТК с межд. участием: «ПИТ-2006» Том 2. 2006 г. Самара. стр. 113-118.
Ватолин Д.С., Алгоритмы Сжатия изображений, Издательский отдел факультета Вычислительной Математики и Кибернетики МГУ им. М.В. Ломоносова, 1999 г. Стр. 21.