Введение. Давление представляет собой важный информативный параметр многих физических процессов. Задача измерения давления решается разнообразными измерительными приборами, важным классом которых являются датчики давления. Датчики давления основываются на различных принципах, среди них большую долю занимает тензорезистивный принцип измерения [1].
Преимуществом тензорезистивных датчиков давления является сравнительно низкая нелинейность, недостатком – значительная температурная погрешность. Непрерывно растущие требования к точности измерительной информации диктуют необходимость коррекции погрешностей тензометрических датчиков давления. Аналоговые методы коррекции погрешностей, основанные на аналоговых схемотехнических решениях, например, изложенные в [2, 3], не позволяют достичь высоких метрологических характеристик, поэтому в последние несколько лет все шире применяются цифровые методы коррекции погрешностей, выполняемые цифровыми вторичными преобразователями датчиков давления.
Алгоритмы коррекции нелинейности и температурной погрешности. Алгоритмы коррекции нелинейности и температурной погрешности, выполняемые цифровыми вторичными преобразователями сигналов тензометрических датчиков давления, основываются на математических моделях измерительных сигналов датчиков. Эти модели отражают существенные взаимосвязи между значениями измеряемой величины, значениями внешних воздействующих факторов и значениями выходного сигнала датчика.
Наибольший вклад в дополнительную погрешность тензометрических датчиков давления вносит температура. Влияние температуры вызывает изменение начального сигнала (аддитивная составляющая температурной погрешности) и чувствительности (мультипликативная составляющая) датчиков. Для коррекции температурной погрешности применяется метод вспомогательных измерений [4], заключающийся в добавлении чувствительного элемента температуры в структуру датчика давления. Требования к характеристикам чувствительного элемента температуры, а также теоретическая оценка нижней границы неисключенной температурной погрешности датчика давления исследованы в [5]. Измерительные сигналы давления и температуры подаются на АЦП, расположенный во вторичном преобразователе.
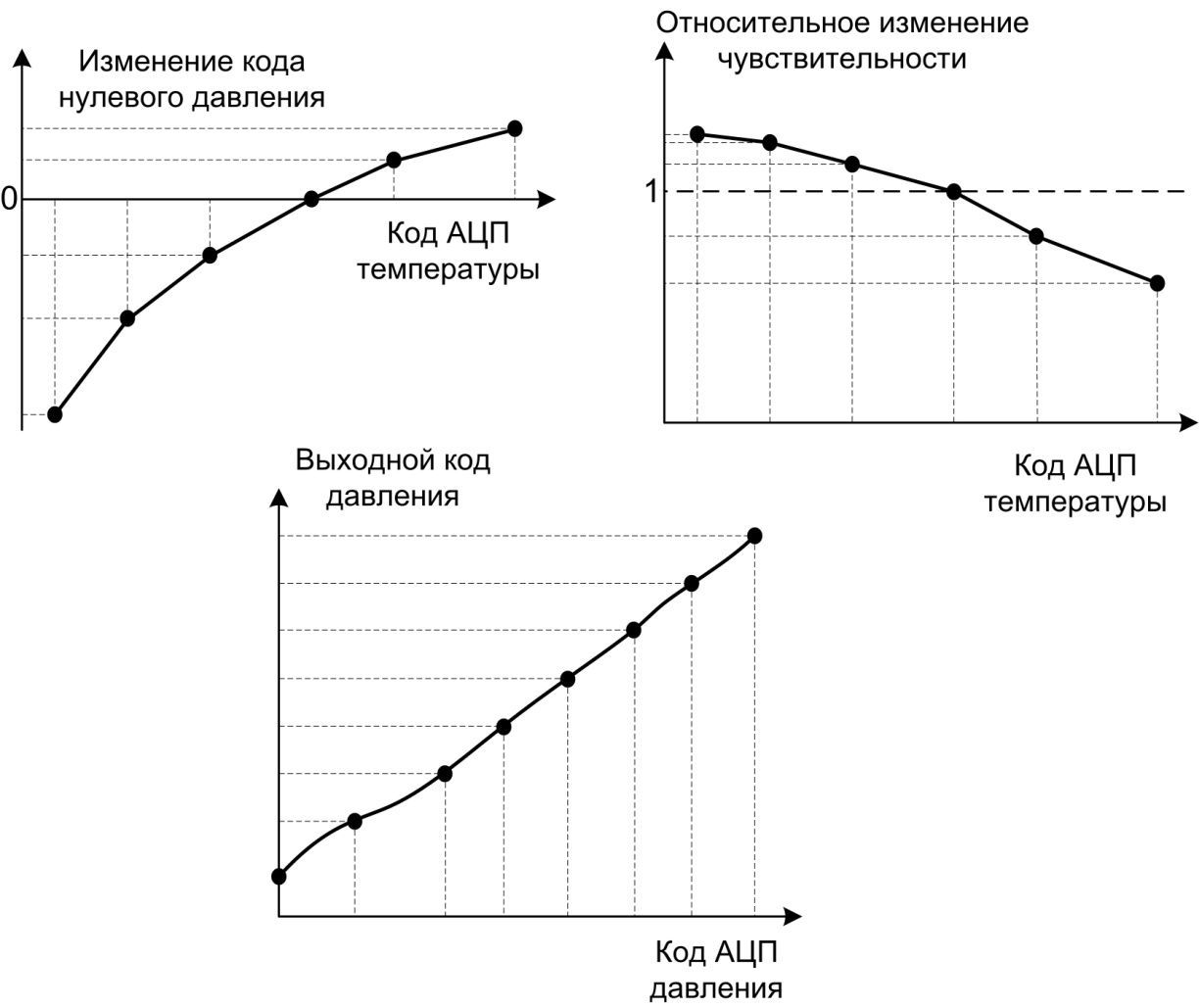
Зависимости изменений кодов АЦП начального сигнала от кодов АЦП температуры и относительных изменений чувствительности от кодов АЦП температуры, а также зависимость кодов АЦП давления от давления определяются экспериментально на этапе совместной настройки датчиков и вторичных преобразователей, после чего аппроксимируются полиномами первой-третьей степеней либо кубическими сплайнами. Следует отметить, что аппроксимируется не сама зависимость кодов АЦП давления от давления, а обратная ей зависимость выходных кодов давления от кодов АЦП давления (рисунок 1).
Рисунок 1 – Модель измерительных сигналов тензорезистивных датчиков
Алгоритм коррекции нелинейности и температурной погрешности заключается в последовательном вычислении поправок для коррекции аддитивной и мультипликативной составляющей температурной погрешности, внесении их в результат измерения давления и коррекции нелинейности с одновременным нормированием сигнала к заранее заданным пределам изменения выходного кода давления. Для случая аппроксимации температурных характеристик полиномами второй степени и градуировки – кубическим сплайном пример реализации алгоритма на языке Си показан ниже.
// Вычислить поправку для коррекции аддитивной составляющей
dx = EvalParabola(t,AddParabola);
// Вычислить поправку для коррекции мультипликативной составляющей
k = EvalParabola(t,MultParabola);
// Вычислить промежуточный код давления
dp_t = ((dp - dx) - ZeroNcc)*k + ZeroNcc;
// Вычислить выходной код
Out_code = EvalSpline(dp_t,9,Grad,SG);
Подобный алгоритм изложен в [6] и может одинаково успешно применяться в датчиках абсолютного и избыточного давлений, а также в датчиках односторонней разности давлений. Для датчиков знакопеременной разности давлений рассмотренный алгоритм неприменим, потому что в таких датчиках, во-первых, начальному сигналу соответствует средняя точка градуировочной характеристики, а во-вторых, имеется две мультипликативных составляющих температурной погрешности (для положительного и отрицательного пределов измерений), в общем случае не подобных друг другу. Поэтому при коррекции погрешностей таких датчиков аппроксимируется зависимость изменений средней точки градуировки от кодов АЦП температуры и две зависимости относительных изменений чувствительности. Ниже приведен пример реализации алгоритма для случая аппроксимации всех характеристик кубическими сплайнами.
// Вычислить поправку для коррекции аддитивной составляющей
fx = SplineAdd(temp);
// коррекция аддитивной составляющей
adc_code -= fx;
// условие расчета коэффициента коррекции мультипликативных составляющих
if(adc_code >= ZERO_NCC_DP)
k = SplineMultPos(temp);
else if(adc_code < ZERO_NCC_DP)
k = SplineMultNeg(temp);
// коррекция мультипликативной составляющей
adc_code = (adc_code - ZERO_NCC_DP)*k + ZERO_NCC_DP;
// Вычислить выходной код
Out_code = SplineGrad(adc_code);
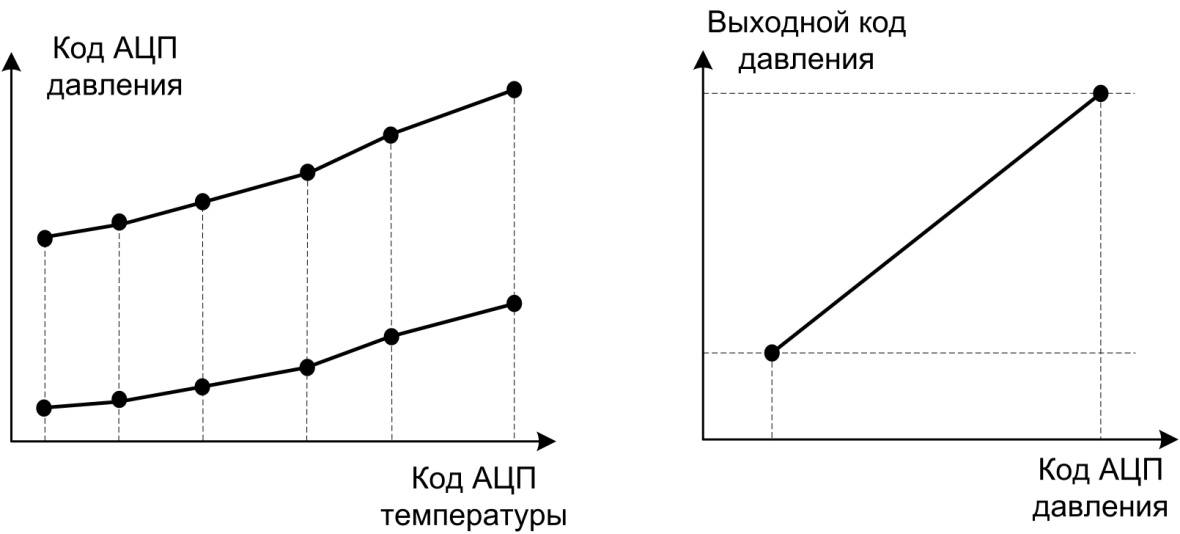
В тех случаях, когда датчик давления имеет низкую нелинейность, и требуется корректировать только температурную погрешность, целесообразно применять другой алгоритм, который заключается в аппроксимации температурных зависимостей нулевого и номинального сигналов полиномами или сплайнами и линейной аппроксимации градуировочной характеристики (рисунок 2):
Рисунок 2 – Модель измерительных сигналов датчика давления с линейной градуировочной характеристикой
На первом шаге алгоритма по коду АЦП температуры вычисляются коды АЦП нулевого и номинального давлений в текущей температуре, на втором шаге полученные коды принимаются за абсциссы концов отрезка, ординаты которых строго фиксированы, вычисляются коэффициенты прямой, используемые при вычислении выходного кода давления. Пример реализации такого алгоритма для случая аппроксимации полиномами третьей степени приведен ниже:
// Вычислить код нулевого давления в текущей температуре
N0 = EvalPoly3(temp,ZeroPoly3);
// Вычислить код номинального давления в текущей температуре
NN = EvalPoly3(temp,NominalPoly3);
// Коррекция температурной погрешности
// и вычисление выходного кода
Out_code = EvalOutCode(adc_code,N0,NN);
Анализ вычислительных затрат на реализацию алгоритмов аппроксимации характеристик тензометрических датчиков давления проведен в работе [7]. Показано, что вычисление коэффициентов аппроксимирующих кривых встроенным программным обеспечением вторичных преобразователей после включения питания целесообразно и занимает вполне приемлемое время – порядка единиц-десятков миллисекунд – с учетом того обстоятельства, что время готовности датчиков к работе обычно составляет единицы-десятки минут.
Методика автоматизированной настройки тензометрических датчиков давления изложена в работе [8], основана на вычислении коэффициентов аппроксимирующих функций встроенным программным обеспечением вторичных преобразователей и позволяет радикально снизить трудоемкость совместной настройки датчиков и вторичных преобразователей по сравнению с методикой, изложенной в [6], за счет реализации командного режима работы вторичных преобразователей с арбитражем по номерам датчиков и проведения одновременной настройки нескольких (до 30) экземпляров датчиков на одинаковый предел измерений.
Заключение. Рассмотренные алгоритмы коррекции температурной погрешности и нелинейности тензометрических датчиков давления цифровыми вторичными преобразователями применимы к любым типам тензометрических датчиков – к полупроводниковым датчикам, к тонкопленочным и другим. Датчики давления, оснащенные цифровыми вторичными преобразователями со встроенным программным обеспечением, выполняющим описанные алгоритмы, обладают высокими метрологическими характеристиками. Основная погрешность таких датчиков не превышает величины 0,1 %.
Следует отметить, что свойственные тензометрическим датчикам погрешности вариации и гистерезиса не могут быть скорректированы рассмотренными алгоритмами. Вариацию и гистерезис следует устранять конструктивно-технологическими методами.
Литература:
Проектирование датчиков для измерения механических величин / Под ред. Е.П. Осадчего. – М.: Машиностроение, 1979 г. – 480 с., ил.
Мартынов Д.Б., Стучебников В.М. Температурная коррекция тензопреобразователей давления на основе структур КНС // Датчики и Системы, №10, 2002, с. 6-12.
Тихоненков Е.В., Мишин В.А. Схемная минимизация аддитивной температурной погрешности тензорезисторных датчиков давления с мостовой измерительной цепью // Датчики и Системы, № 3, 2006, с. 14 - 17.
Земельман М.А. Автоматическая коррекция погрешностей измерительных устройств / М.: Изд-во стандартов, 1972 г. – 199 с.
Катков А.Н. Оценка достижимой погрешности цифровых датчиков и необходимой чувствительности измерения влияющих факторов // Известия Смоленского государственного университета, №2, 2011, с. 140-146.
Горбунов С.Ф., Цыпин Б.В. Линеаризация градуировочных характеристик емкостных датчиков давления // Измерительная техника, № 10, 2010, с. 23-25.
Катков А.Н. Анализ вычислительной сложности алгоритмов аппроксимации характеристик чувствительных элементов цифровых датчиков / Информационно-измерительная техника: межвуз. сб. науч. тр. Под ред. д.т.н., проф. Е.А. Ломтева. Вып. 36. – Пенза, Изд-во ПГУ, 2011. – 215 с., с. 166-177.
Катков А.Н. Методика автоматизированной настройки цифровых датчиков // Проблемы автоматизации и управления в технических системах: тр. Междунар. науч.-техн. конф. (г. Пенза, 19-22 апреля 2011) : в 2 т. / под ред. д.т.н., профессора М.А. Щербакова. – Пенза: Изд-во ПГУ, 2011. – 1 т. 318 с. с. 275-276.