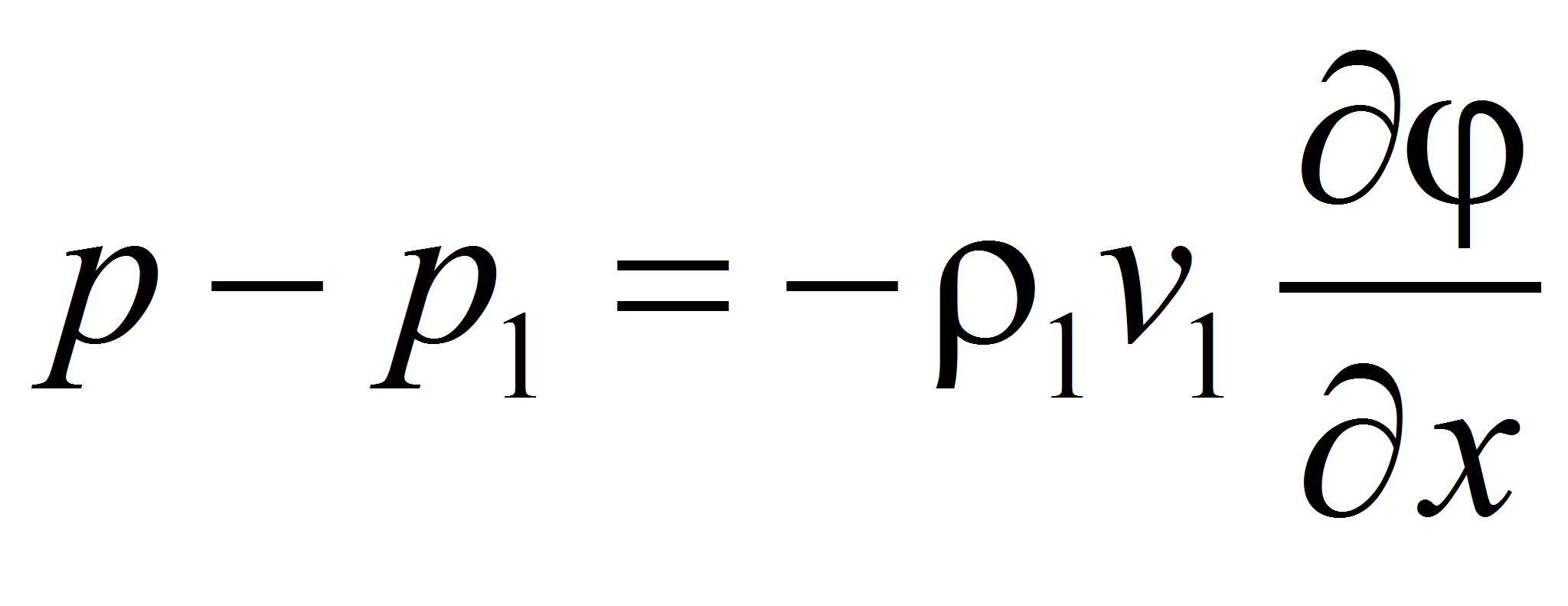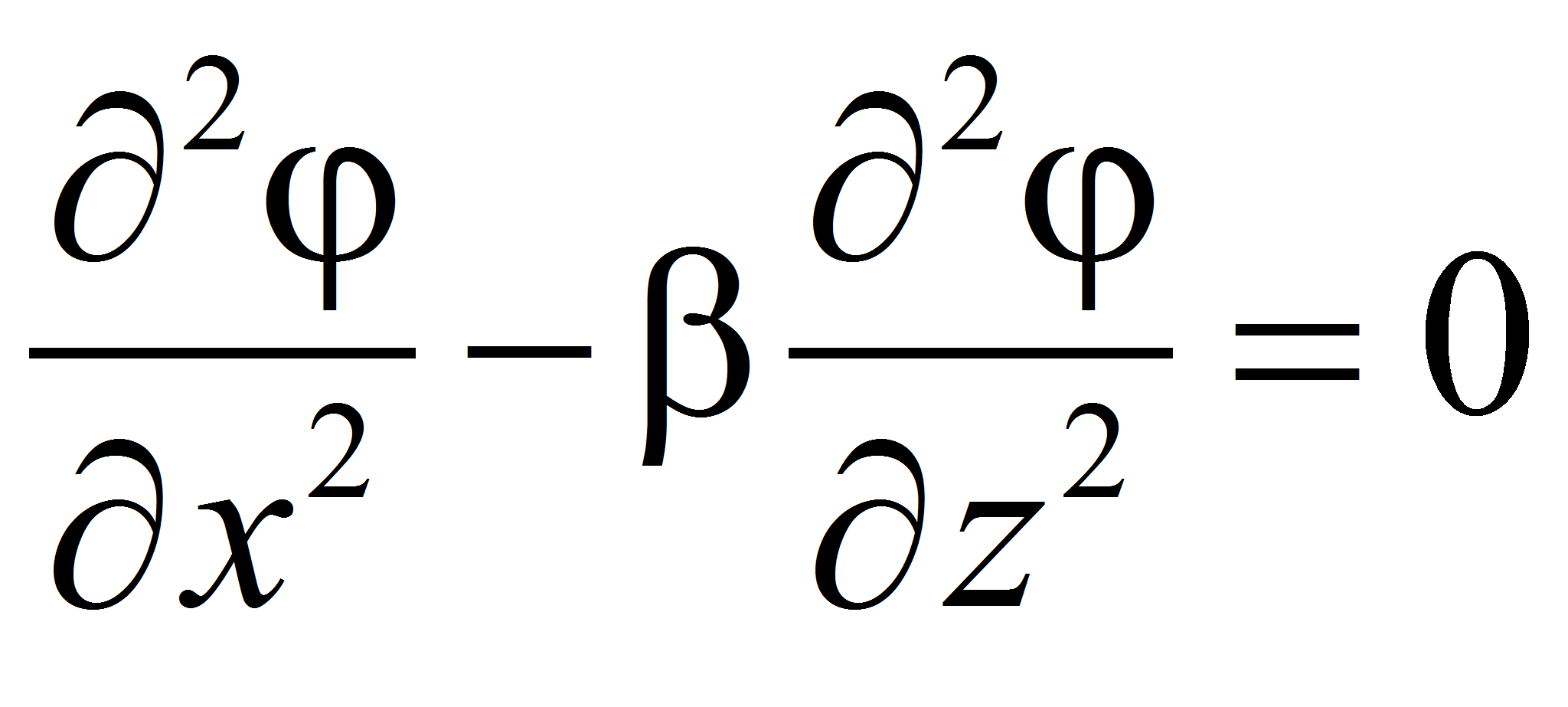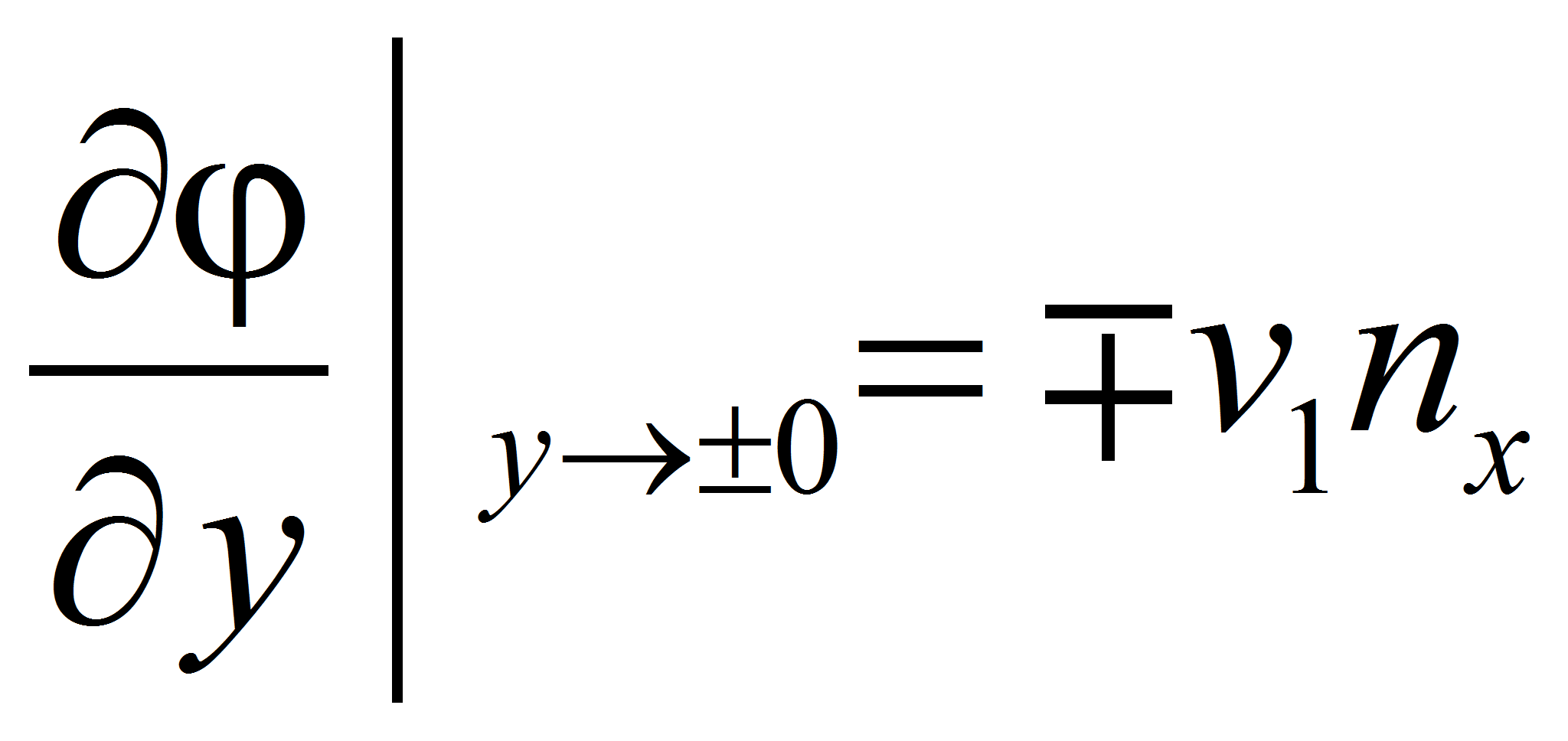Рассматривается математическая модель, описывающая силы подъема и сопротивления крыла самолета (или другого летательного аппарата), обтекаемого сверхзвуковым потоком сжимаемого газа. Описанные математические методы можно использовать не только в гидроаэромеханике, но и во многих областях естественных наук, при этом для корректности его использования требуется выполнение критерия сплошности среды.
При обтекании сверхзвуковым газовым потоком твёрдого тела на его передней кромке образуется ударная волна, причем не всегда единственная. Количество таких волн зависит от формы тела. Математически уравнения идеальной гидроаэромеханики допускают разрывные решения, т.е. решения, которые имеют скачки параметров газа (плотности, давления, скорости и температуры). Одним из таких проявлений в природе является образование ударной волны около летящего со сверхзвуковой скоростью тела в плотных слоях атмосферы Земли. Например, около летающих сверхзвуковых самолетов или около метеоритов, вторгающихся в плотные слои атмосферы Земли с большими сверхзвуковыми скоростями. В условиях космического пространства хорошо известны межпланетные ударные волны, являющиеся чаще всего результатом активных процессов на Солнце (например, вспышек).
Часто важные в приложениях задачи рассматривают на основе уравнений гидроаэромеханики идеальной жидкости, а не на полных уравнениях. Это связано с тем, что математически такие уравнения существенно проще. Если нужно определить подъемную силу крыла самолета при малых дозвуковых скоростях, то вязкие силы пренебрежимо малы и нет необходимости использовать уравнения Навье – Стокса. Однако для определения сопротивления такого крыла при движении его в воздухе вязкие силы оказываются определяющими и необходимо использовать более сложный математический аппарат, связанный с уравнениями Навье – Стокса.
При обтекании твердого тела воздушный поток подвергается деформации, что приводит к изменению скорости, давления, температуры и плотности в струе потока. Таким образом, около поверхности обтекаемого тела создается область переменных скоростей и давлений воздуха. Наличие различных по величине давлений у поверхности твердого тела приводит к возникновению аэродинамических сил и моментов. Рассмотрим воздействие аэродинамических сил и моментов на крыло самолета, обтекаемое сверхзвуковым потоком сжимаемого газа.
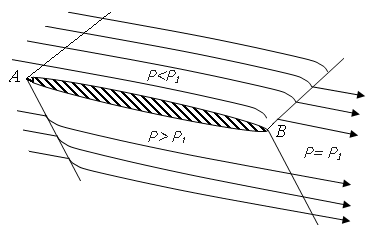
Рассмотрим для простоты сферическое тело радиуса R (рис. 1.),
перемещающееся в воздухе со сверхзвуковой скоростью. Впереди него
образуется ударная волна В, являющаяся границей между
областями 1 и 2, которые отличаются значениями параметров газа.
Направим ось Оx вдоль скорости потока газа и обозначим через
![]() и
и
![]() – скорость, давление, плотность и температура в невозмущенном
телом потоке газа, т.е. до ударной волны.
– скорость, давление, плотность и температура в невозмущенном
телом потоке газа, т.е. до ударной волны.
Рис. 1. Обтекание сферического тела радиуса R сверхзвуковым потоком газа
В область 1 возмущения от тела не попадают, т.к.
тело движется со сверхзвуковой скоростью. Так как скорость газа в
лобовой точке тела А обращается в нуль, то от точки А
до точки С на ударной волне есть область дозвуковой скорости
газа, которой достигают возмущения воздуха от летящего тела.
Физический смысл образования ударной волны заключается в разделении
невозмущенного и возмущенного потоков газа. Если через
![]() и
и
![]() обозначить скорость, давление, плотность и температуру газа
соответственно сразу после ударной волны В, то справедливы
неравенства:
обозначить скорость, давление, плотность и температуру газа
соответственно сразу после ударной волны В, то справедливы
неравенства:
Здесь B – головная ударная волна, А – критическая точка на теле, в которой скорость обращается в нуль, С – точка на ударной волне и на оси симметрии Ox, 1 и 2 – области течения перед и за ударной волной.
Это означает, что скорость за ударной волной уменьшается, а давление, плотность и температура возрастают.
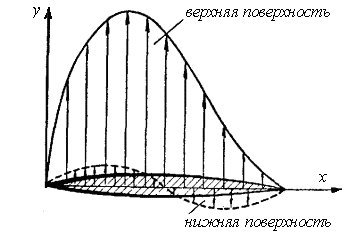
Рис. 2. Распределение давления
Сильным возрастанием температуры за ударной волной и объясняется оплавление возвращающихся на Землю космических аппаратов и метеоритов, вторгающихся в атмосферу с большими сверхзвуковыми скоростями. Такие ударные волны называются волнами сжатия (плотность газа возрастает). Заметим, что в природе никогда не наблюдались ударные волны разрежения, в которых плотность падает. Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена. Распределение давления находится по формуле:
Соотношения между параметрами с индексами «1» и «2» можно получить из интегральных законов сохранения массы, импульса и энергии, поскольку они справедливы и для разрывных функций. Такие соотношения называются соотношениями Гюгонио. Вместе с уравнением состояния они позволяют определить значения параметров газа за ударной волной (индекс «2») по значениям параметров невозмущенного ударной волной потока газа (индекс «1»).
Описанный математический аппарат можно использовать в различных прикладных технических задачах при условии выполнения критерия сплошности среды, т.е. для газов, например, длина свободного пробега частиц должна быть много меньше характерных размеров рассматриваемых объектов обтекания. В частности, в условиях космического пространства часто среда очень разрежена. В таких средах длина свободного пробега частиц очень велика, но размеры самих объектов исследования оказываются во многих случаях существенно больше, т.е. данные методы применимы и к таким объект.
Действующая на тело сила сопротивления есть не что иное, как уносимая звуковыми волнами в единицу времени х – компонента импульса.
Рис. 3. Действие сил на крыло летательного аппарата
Фронт ударной волны по мере удаления от аппарата постепенно принимает почти правильную коническую форму, перепад давления на нём уменьшается с увеличением расстояния от вершины конуса, и ударная волна превращается в звуковую. Угол между осью и образующей конуса α связан с числом Маха M соотношением
- На рисунке 4 изображена коническая форма фронта ударной волны при перемещении вдоль летательного аппарата.
Рис. 4. Коническая форма фронта ударной волны
Сверхзвуковое обтекание заостренного тела описывается уравнением в частных производных типа одномерного волнового уравнения
- с граничными условиями в упрощенном случае вида:
- Методом Даламбера можно найти общее решение одномерного волнового уравнения (2). Оно имеет вид
- Для однозначной разрешимости данное решение необходимо удовлетворить граничным условиям (3). Авторами решены аналитически и рассчитаны с помощью ИТ различные постановки задач, возникших по данной теме.
Таким образом можно определить силу сопротивления и подъемную силу крыла самолета, обтекаемого сверхзвуковым потоком сжимаемого газа. Оно должно иметь заостренные как заднюю, так и переднюю кромки, быть очень тонким с большим размахом, и с постоянным вдоль размаха профилем сечения. Подъемная сила у крыла определяется одним только углом атаки и не зависит от формы его сечения.
- Литература:
- Покорная О.Ю., Афанасьев И.В. Математическое моделирование сверхзвукового обтекания крыла самолета потоком сжимаемого газа, Всероссийская научн.-техн. конференц. «Перспектива_10». Воронеж. ВАИУ, 2010. с. 97-101
Баранов В.Б. и Краснобаев К.В., Гидродинамическая теория космической плазмы. М.: Наука, 1977. 256 с.
Белолипецкий В.Ю., Костюк Ю.И., Шокин Ю.И. Математическое моделирование течений стратифицированной жидкости. Новосибирск: Наука. Сиб. отд, 1991.162 с.