Перед строительством любого объекта необходимо решить ряд задач, связанных с его будущей эксплуатацией. Одной из важнейших задачей является обеспечение требуемого уровня пожарной безопасности. Для решения этой задачи уже долгое время используются упрощенные интегральные методы расчета, которые из-за своих грубых приближений, не позволяют в полной мере оценить угрозу для жизни людей. Современный уровень развития теории тепломассообмена позволил создать математическую модель пожара. А развитие компьютерных технологий позволило создать компьютерную модель пожара.
По степени детализации описания термогазодинамических параметров пожара можно выделить три типа детерминистических моделей: интегральные, зонные (зональные) и полевые [1].
Интегральный (однозонный) метод является наиболее простым среди существующих методов моделирования пожаров. Суть интегрального метода заключается в том, что состояние газовой среды оценивается через осредненные по всему объему помещения термодинамические параметры. Соответственно, температура ограждающих конструкций и другие подобные параметры оцениваются, как осредненные по поверхности.
Однако если газовая среда характеризуется значительной неоднородностью, то информативность интегрального метода может оказаться недостаточной для решения практических задач. Подобная ситуация обычно возникает на начальной стадии пожара и при локальных пожарах, когда в помещении наблюдаются струйные течения с явно выраженными границами и, кроме того, существует достаточно четкая стратификация (расслоение) среды.
Таким образом, область применения интегрального метода, в которой предсказанные моделью параметры пожара можно интерпретировать как реальные, практически ограничивается объемными пожарами, когда из-за интенсивного перемешивания газовой среды локальные значения параметров в любой точке близки к среднеобъемным. За пределами возможностей интегрального метода оказывается моделирование пожаров, не достигших стадии объемного горения и, особенно, моделирование процессов, определяющих пожарную опасность при локальном пожаре. Наконец, в ряде случаев даже при объемном пожаре распределением локальных значений параметров пренебрегать нельзя.
Более детально развитие пожара можно описать с помощью зонных (или зональных) моделей, основанных на предположении о формировании в помещении двух слоев: верхнего слоя продуктов горения (задымленная зона) и нижнего слоя невозмущенного воздуха (свободная зона). Таким образом, состояние газовой среды в зональных моделях оценивается через осредненные термодинамические параметры не одной, а нескольких зон, причем межзонные границы обычно считаются подвижными.
Однако при создании зонных моделей необходимо делать большое количество упрощений и допущений, основанных на априорных предположениях о структуре потока. Такая методика неприменима в тех случаях, когда отсутствует полученная из пожарных экспериментов информация об этой структуре, и, следовательно, нет основы для зонного моделирования. Кроме того, часто требуется более подробная информация о пожаре, чем осредненные по слою (зоне) значения параметров.
Полевые модели, обозначаемые в зарубежной литературе аббревиатурой CFD (computational fluid dynamics), являются более мощным и универсальным инструментом, чем зональные, поскольку они основываются на совершенно ином принципе. Вместо одной или нескольких больших зон, в полевых моделях выделяется большое количество (обычно тысячи или десятки тысяч) маленьких контрольных объемов, никак не связанных с предполагаемой структурой потока. Для каждого из этих объемов с помощью численных методов решается система уравнений в частных производных, выражающих принципы локального сохранения массы, импульса, энергии и масс компонентов. Таким образом, динамика развития процессов определяется не априорными предположениями, а исключительно результатами расчета.
Естественно, что такие модели, по сравнению с интегральными и зональными, требуют значительно больших вычислительных ресурсов. Однако в последние двадцать лет, в связи с быстрым развитием компьютерной техники, полевые модели из чисто академической концепции превратились в важный практический инструмент.
В основу модели заложено решение трехмерных нестационарных уравнений законов сохранения масс, импульса и энергии [2].
Уравнение сохранения массы:
.
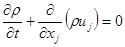Уравнение сохранения импульса
.
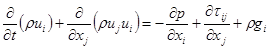Для ньютоновских жидкостей, подчиняющихся закону Стокса, тензор вязких напряжений определяется выражением
.
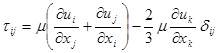Уравнение энергии
,
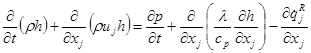где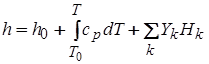 
– статическая энтальпия смеси;
Hk – теплота образования k-го компонента;
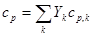– теплоемкость смеси при постоянном давлении;
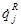– радиационный поток энергии в направлении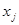 
Уравнение сохранения химического компонента k:
.
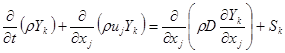Для замыкания системы уравнений используется уравнение состояния идеального газа. Для смеси газов оно имеет вид:
.
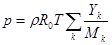где R0 –универсальная газовая постоянная;
Mk – молярная масса k-го компонента.
Уравнения турбулентности:
,
,
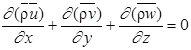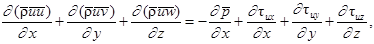
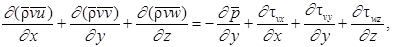
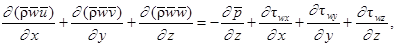
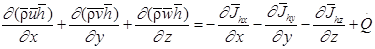где
,
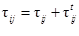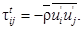
Кинетическая энергия турбулентности k связана с турбулентными флуктуациями компонент скорости следующим образом:
.
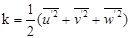Эффективная турбулентная вязкость meff определяется с помощью двух турбулентных параметров: скорости турбулентности ut и характерного масштаба l по соотношению
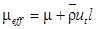или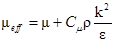 
.
Решение уравнения переноса лучистой энергии базируется на P1 аппроксимации метода сферических гармоник для серой двухфазной двух температурной среды. Достоинством этого метода является его легкая совместимость с методами расчета аэродинамики и теплопереноса, реализованными на криволинейных сетках:
.
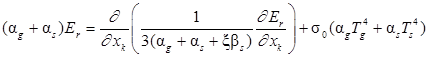Расчет химической кинетики горения топлива основан на использовании глобальных необратимых реакций между горючими и окислителем:
,
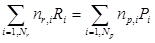где nr,i – стехиометрический коэффициент реагента; np,i - стехиометрический коэффициент продукта; Ri – i-ый реагент; Pi – i-ый продукт.
Сохранение массы:
,
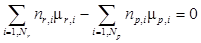где μi – молярная масса компонента.
Моделирование проводится с учетом множества параметров, основными из которых являются свойства пожарной нагрузки, теплофизические свойства материалов ограждающих конструкций, действия систем дымоудаления, вентиляции и пожаротушения [3].
Модель позволяет предсказать наихудший для безопасности людей вариант развития пожара. Это свойство используется для определения необходимого времени эвакуации людей, выдачи рекомендаций по повышению пожарной безопасности объекта, проведения экспертизы объемно-планировочных и конструктивных решений [4].
В настоящее время создан целый ряд компьютерных программ (FDS, Sigma-Fire, Phoenics, Smartfire, Sofie), реализующих полевой метод моделирования, которые достаточно точно описывают поля скоростей, температур и концентраций на начальной стадии пожара.
Таким образом, использование современного программного обеспечения для математического моделирования динамики параметров пожара позволяет не только провести оценку пожарной опасности конструкций, зданий и сооружений, но также выявить проблемные зоны на ранней стадии строительства объекта, провести оценку риска на стадии проектирования и своевременно разработать превентивные мероприятия по обеспечению противопожарной защиты.
Литература:
1. ГОСТ 12.1.004-91. Пожарная безопасность. Общие требования.
2. Пузач С.В., Смагин А.В., Лебедченко О.С., Абакумов Е.С. Новые представления о расчете необходимого времени эвакуации людей и об эффективности использования портативных фильтрующих самоспасателей при эвакуации на пожарах. Монография. - М.: Академия ГПС МЧС России, 2007. 222 с.
3. Кошмаров Ю. А. Прогнозирование опасных факторов пожара в помещении: Учебное пособие.- М.: Академия ГПС МВД России, 2000. 118 с.
4. Литвинцев К. Ю., Серебренников Д. С., Моделирование задымленности помещения при пожаре // Актуальные проблемы пожарной безопасности: Материалы XXII Международной научно-практической конференции, Ч.1. Москва: ВНИИПО, 2010, с. 49-51
