Рациональное инвестирование средств является важной задачей, стоящей перед инвесторами. Она важна как для инвесторов, так и для народного хозяйства в целом. Задачи формирования оптимальных (в том или ином смысле) портфелей из инвестиционных проектов рассматривались многими исследователями [1, с.21; 2, с.235; 3, с.17; 4, с.48; 5,с.230; 6,с.800]. В данной статье рассматривается проблема формирования оптимального инвестиционного портфеля, состоящего из инвестиционных проектов, с учетом групповых платежей.
Задача формирования портфеля
Имеется набор проектов С1, С2 , …, Сm (Ci=(ci0, ci1, …, cin )), из которых инвестору необходимо выбрать некоторые инвестиционные проекты (потоки платежей) для финансирования. Инвестиционный проект Сi= (ci0 , ci1 , … , cin) это вектор, у которого первая ненулевая компонента, если такие существуют, отрицательная, а последняя ненулевая компонента положительная. Компонент вектора cij– сумма платежа или возврата средств по проекту iв момент времени j. Будем считать, что все проекты сосредоточены на общем временном интервале, для этого, при необходимости, можно дополнить проекты нулевыми платежами. При этом предполагается возможная зависимость между некоторыми проектами, т.е. выбор проекта для включения в портфель зависит от того, с какими проектами он связан. Зависимость можно представить в виде ориентированного графа, где вершинам соответствуют проекты, а ребра определяют зависимость между проектами таким образом, что для включения в портфель некоторого проекта необходимо включение и его предшественников. После ряда преобразований [12,c.56;13,c.174;14,c.108] задача сводится к частично целочисленной задаче линейного программирования.
Найти числа
х1,…, хmÎ{0,1};
y1,…,ysÎ{0,1};
F1,…,FnÎR
такие, что
yj³xi при iÎUj;
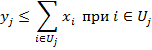
хi≥ хk
для зависимых проектов;
F k+1£qFk при k=0,1,…,n-1;
Fk+1£rFk при k=0,1,…,n-1;
Fn® max
Приближенные методы решения
Для решения задачи применялись следующие эвристические методы:.
Модифицированный метод ветвей и границ
Применялся следующий эвристический прием, адекватный структуре задачи. Применим метод ветвей и границ к множеству проектов U1, в результате получим портфель П1. Затем применим тот же метод к множеству проектов U2 при условии, что в портфель уже вошли проекты из П1. В результате получим портфель П2ÉП1. Продолжая этот процесс, после (s+1) шагов получим портфель П (проекты, не входящие ни в одно из множеств Uj, анализируются на последнем шаге) . Такой прием достаточно эффективен, если множества Uj не являются ни слишком большими, ни слишком малыми непересекающихся множествах Uj равного размера сложность вычислений можно оценить числом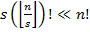 
, где s – число множеств.
Алгортм решения
Шаг 1. Для j от 1 до s выполнять:
1.1 Вход: Ci, Uj, q, r, m, k. Проверка: если Uj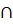
Пj, то рассматриваются для включения в портфель только те проекты, из множества Uj, которых нет в множестве Пj. Применяется стандартный метод ветвей и границ ко множеству Uj.
Выход: Портфель Пj, капитал инвестора Rbest.Если j=s, то переход к шагу 2, иначе →шаг 1.2.
1.2 Вход:Пj, Пj+1. Пj+1+Пj →шаг 1.1.
Выход: Пj+1.
Шаг 2. Если есть Ci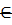
Uj, то применяется стандартный метод ветвей и границ к оставшемуся множеству проектов. Конец алгоритма [7,с.36; 8,с.85; 11, с.253].
Эволюционный алгоритм (1+1)-ЕА [9, с.57; 10, с. 182; 12, с.56]
Для описания этого алгоритма рассмотрим следующие термины.
· Особь (индивидуум) – инвестиционный портфель.
· Хромосома – приоритетный список проектов .
· Популяция – в данном алгоритме состоит из одной особи.
· Воспроизведение (оператор репродукции) – репродукция особи, т.е. формирование портфеля на основе текущего приоритетного списка.
· Отбор (оператор селекции). Применяется так называемый элитный отбор, то есть из всех особей отбираются особи с наибольшим возможным капиталом на конец временного горизонта.
· Оператор мутации. Проекты в приоритетном списке меняются местами случайным образом. В результате получается новая хромосома.
Алгоритм решения
Вход:
· Множество проектов С1, С2, С3…Сn;
· Начальный капитал инвестора F-1;
· Подмножества Uj;
· Множество векторов платежей Pj;
· Ставки q и r;
· Приоритетный список проектов П;
· Port – инвестиционный портфель;
· F-итоговый капитал текущего портфеля;
· FBest – лучший итоговый капитал;
Шаг 1.1: для i=1 до n выполнять: рассчитывается NPV каждого проекта по формуле NPV=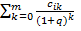
+∑((
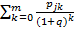)/ N(Uj) )
Шаг1. 2: для i=1 до n выполнять: в приоритетный список П записываются номера проектов в порядке убывания их NPV.
Шаг 2: Воспроизведение
2.1 для i=1 до n выполнять: Port:=П[i] \\ в текущий портфель помещается проект из приоритетного списка П.
2.2 рассчитывается F для этого портфеля по формуле: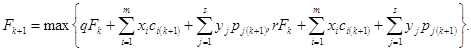
Шаг 3: Селекция
3.1 если F> FBest, то FBest:=F и переход к шагу 2,
3.2 если F≤ FBest, то последний проект из портфеля Port возвращаем в конец списка П и переход к шагу 2,
3.3 если F≤ FBest два или более раз, то переход к шагу 4.
3.4 если F≤ FBest больше Z раз, то конец алгоритма.
Шаг 4: Мутация - случайная перестановка элементов в списке П с помощью наивного алгоритма: Из приоритетного списка П оператор random случайным образом выбирает 1 элемент, он ставится в начало списка Пnew, эта процедура повторяется до тех пор, пока в список П не станет пустым. Переход к шагу 2.
Выход: FBest - лучший итоговый капитал, Port - инвестиционный портфель.
На базе представленных алгоритмов был разработан программный продукт, с помощью которого был проведен численный эксперимент, показавший следующие результаты: модифицированный метод ветвей и границ и эволюционная стратегия показали хорошие результаты в соотношении время работы/точность, в частности, точность упрощенного метода 97%, а эволюционной стратегии 88% при практически тех же временных затратах.
Работа выполнена при поддержке РФФИ (проект 07-06-00021).
Литература:
4. Бронштейн Е.М. (2004): Оптимальные инвестиционные портфели // Системное моделирование социально – экономических процессов. М.: ЦЭМИ РАН.
5. Balinski M.L. (1970): On a Selection Problem // Management Science. v.17. №11.
7. Корбут А.А., Сигал И.Х., Финкельштейн Ю.Ю., Об эффективности комбинаторных методов в дискретном программировании. М.: Наука,1979.
8. Сигал И.Х., Иванова А.П., Введение в прикладное дискретное программирование. М.:Физматлит, 2007.
9. Батищев Д.Ю. Генетические алгоритмы решения экстремальных задач // учебное пособие под ред. Я.Е.Львовича. Воронеж: Воронежский гос. техн. ун-т; Нижегородский ун-т. 1995.
10. Борисовский П.А., Еремеев А.В. О сравнении некоторых эволюционных алгоритмов // Автоматика и телемеханика, №2, 2004.
12. Муслимова, Г. Р. Дополнительные условия при формировании оптимальных портфелей, состоящих из инвестиционных проектов // Молодой ученый. 2010. №6.
