Теоретическое обоснование технология нарезки аэрационного дренажа в условиях Туркменистана

Для регулирования водно-воздушного режима почвы из-за малого срока службы (2-4 года) кротовый дренаж не получил широкого применения. Однако разрушение кротового дренажа зависит не только от механического состава почв, но и их конструктивных, технологических параметров рабочего органа дренажной машины и режимов ее функционирования [6,7].

Обзор и анализ существующих конструкции аэрационного дренажа (АД) свидетельствует об эффективности его применения на тяжелых почвах [1,2,3,4,5,6,7,8]. Особенно положительное воздействие на качественный характер почвы оказывает АД на староорошаемых землях, подверженным многократным проходам сельскохозяйственной техники, приводящей к образованию уплотненной подплужной зоны. Важно отметить, что в процессе нарезки АД данной конструкции кротовины склонны к заилению за счет фильтрационного потока через щель, сформированную ножом рыхлителя-кротователя. Основным недостатком данных конструкции является формирование кротовин непосредственно под щелью, что весьма неэффективно из-за плохой устойчивости свода кротовин фильтрационному потоку [4,5]. Наряду с этим формирование уплотненной околодренной зоны снижает коэффициент фильтрации. Процесс полива приводит к разрушению структурных связей в результате набухания грунта плужной уплотненной зоны. Рассмотрим принципиальную схему конструкции АД (рис. 1). Предположим, что дренер в процессе формирования кротовин образует уплотненное ядро придренной зоны толщиной - t.

Максимальное значение гидродинамического давления будет наблюдаться по линии щели и уплотненной зоны. Первые опыты по фильтрации, проведенные А. Дарси  показали, что при ламинарном движении, расход воды определяется по зависимости:   

                                                          Q =k_φ F (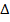H/l)                                                      (1)

где:  Q – расход воды, м³/с; k_φ – коэффициент пропорциональности; F – площадь поперечного сечения, м² ; 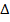H – разность отметок уровней воды, м; l – высота, длина фильтрации, м.

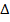H/ l  = i                                      (2)

где: i– гидравлический градиент фильтрации.

Q / F = V_φ                                     (3)

где: V_φ – скорость фильтрации воды.

Вода при фильтрации в грунт  преодолевает все виды гидравлических сопротивлений:  лобовое сопротивление обтекаемых ею твердых частиц; сопротивлению трению о частицы в порах. Данные сопротивления являются тормозящими силами и на их преодоление расходуется напор. Суммарная тормозящая сила равна и прямопротивоположна силе действия на частицы грунта движущейся воды. Данную силу принято называть гидродинамическим или фильтрационным напором. 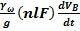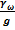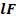В случае притока в кротовую дрену (рис1.) можно определить силу инерции фильтрационного потока в объеме:                                                                       i=  =    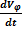                   (4)

где: 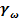 - плотность воды;  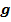- гравитационное ускорение;  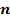– пористость грунта;  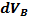/  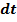- ускорение фильтрации.

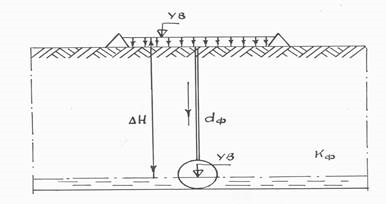
Рис. 1. Схема поступления промывной воды в дрену

            Тормозящая сила движению воды равна:                                    T = 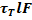                (5)

где: T - тормозящая сила; 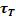 - тормозящая сила в единице объема;  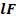- объем грунта.

           Искомое уравнение получим проектируя силы на направление фильтрации:

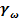H_BF - 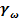H_HF + (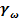/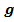) 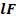a_φ - 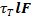  = 0                   (6)        

          Из уравнения (5) тормозящая сила в единице объема равна:                    

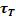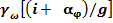      =                                    (7)

         Исходя из этого, что гравитационное ускорение 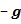 на много порядков выше фильтрационного, им в расчетах принебрегают. Тогда:

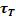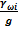 =                                               (8)

          Гидродинамическое давление по величине равно тормозящей силе:

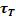                                                                        = d_φ    или                                                        (9)

d_φ= 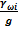                                                               (10)

          Учитывая то, что 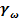   = const;  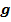 = const, то гидродинамическое давление определяется величиной гидравлического градиента. Исходя из этого, что приток воды в дрену происходит по ее всему периметру, то можно предположить, что плотность скелета гидродинамический взвешенного грунта будет равна:  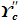   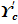  =  - d_φ                              (11)

где: 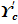 – эффективная плотность скелета грунта.

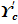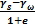 =                                                  (12)

где: e – коэффициент пористости; 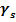  - плотность твердых частиц грунта, тогда:

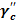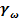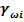                                                                      =  -                или                                    (13)

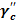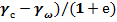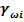 = [(] -                                        (14)

           Анализ зависимости 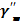 =  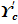- d_φпоказывает, что вынос частиц грунта (суффозия) будет тогда, когда  d_φ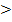 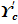  .  При значительном превышении гидродинамического давления / d_φ/ над /  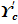/ , то грунт околодренной зоны переходит в плывунное состояние. Таким образом, при выборе конструкции АД необходимо исходить из условия, что эффективная плотность грунта должна быть соизмерима по величине гидродинамическому давлению. При этом для увеличения устойчивости дрен необходимо принять меры по снижению гидродинамического давления. Величину гидродинамического давления определим по формуле:              P_i= 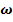_i/ S                       (15)                     

где: 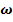_i - гидродинамическая сила;  S– площадь поверхности ядра, на которую действует гидродинамическая сила.                                    

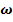      _i = V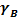 J_P                                      (16)

где: V- объем грунтовый арки (ядра); 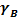  - плотность воды; J_P– разрушающий градиент напора.                                                                                      

                                                                                                 S = 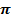 D²                                    (17)

Объем грунтовой арки равен:                                      V= 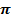 D² t                                  (18)                   

где: t– толщина арки, тогда: 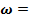 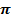                                       D² t 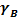 J_P                                 (19)

        Представив значение 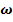 _i и   Sв исходное уравнение получим равенство: 

P_i= t 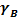 J_P                                  (20)

        Как видно из равенства значениегидродинамического давления прямо пропорционально толщине уплотненного ядра гидравлическому градиенту. Гидродинамическое давление способствует выносу частиц грунта в процесс фильтрационного потока из толщи арки, приводя ее к разрушению. Несущую способность грунтовой арки можно выразить следующим уравнением:

[𝛔] = 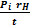                                                             (21)

где: [𝛔] – допустимое напряжение свода грунта арки, (допустимое напряжение свода [𝛔]  грунта арки принимаем равным сопротивлению грунта размыву (С_Р); 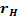 - радиус наружной поверхности арки.

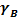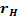           Подставив значение - P_i в уравнение (21) получим:                    С_Р =  J_P      (22)

          Таким образом, сопротивление грунта размыву в основном зависит от градиента и величины радиуса наружной поверхности арки. Следовательно, для увеличения устойчивости дренажной стенки необходимо снизить градиент напора. Градиент напора определяется по зависимости:

J₁ = 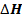 / L                                                     (23)

где: 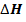– разность напоров;  L- длина пути фильтрации.

          Зависимость (23) показывает, что уменьшение градиента гидравлического напора получаем при увеличении длины пути фильтрации –  L при постоянном значении 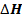. Увеличение длины фильтрации возможно увеличением толщи уплотнительного ядра околодренной зоны или смещением дренажной полости от оси щели. Во втором случае наряду с увеличением пути фильтрации, происходит гашение энергии потока за счет резкого изменения направления движения потока (рис. 2).

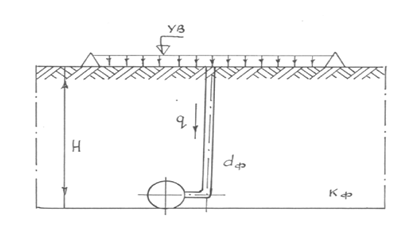
Рис.2. Схема поступления промывной воды в смещенную дрену

           В данном случае градиент напора можно определить по формуле:

J₂  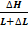=                                                          (24)

где: 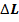 – дополнительная длина пути фильтрационного потока.

        Сравнение гидравлических градиентов  J₁  и  J₂ показывает, что смещение дренажной полости от оси ножевой щели приводит к снижению величины гидравлического градиента. Определение оптимального значения 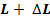  позволить повысить устойчивость полости АД, без снижения эффективности его работы. В случае прокладки двух параллельных АД, где длина междренной зоны равна  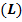степень уплотнения будет зависеть от диаметра АД, междренного расстояния и влажностигрунта (рис.3).

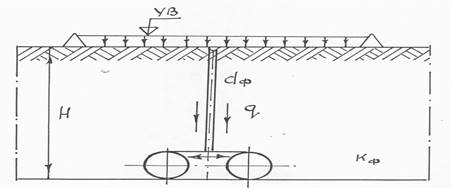
Рис.3. Схема поступления промывной воды в смещенную дрену

Для данного случая закон уплотнения можно сформулировать в следующем виде:

                                                                                     ak= - akdL                                         (25)                                                                               

где: а – коэффициент пропорциональности, зависящий от основных параметров рабочего органа и физико-механических свойств грунта [4,5] (знак /-/ указывает на то, что с увеличением междренного расстояния уплотнение грунта уменьшается); k– снижение уплотнения грунта.

          Примем  ak= α , тогда:                               α= - α dL                                                   (26)

          Интегрируя равенство в пределах от k₀  до k и от  L₀  до L получим:

lnk - lnk₀ = - α L,                                           (27)                                

           откуда                                                            k= k₀ ^-αL                                                 (28)

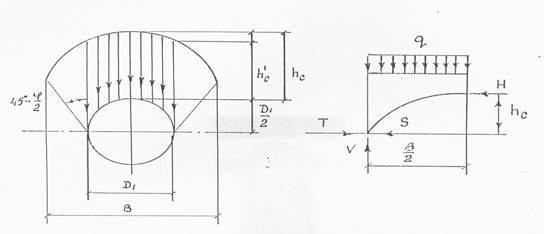
         Таким образом, степень уплотнения грунта зависит от междренного расстояния АД. Известно, что при устройстве закрытой выработки с удалением грунта на большой глубине от уровня земли, поверхности скалывания не распространяются на всю толщу грунта, а соединяются между собой, образуя естественный разгружающей свод. Разгружающий свод очерчивается по параболе  [9]. Применив данное предположение к АД, определим основные нагрузки, действующие на свод кротовой полости (рис.4). При условии предельного равновесия для половины разгружающего свода (рис.5) запишем систему уравнений:

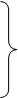                                              ∑ x = 0     H = T = fV

                                              ∑ y = 0     V = 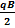                                                                         (29)

                                              ∑ M_A= 0 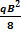    - Hh_c= 0

где: H– реакция отброшенной половины свода;  VиT– составляющие опорной реакции свода; T– сила трения:                                                                 T= fV                              (30)

где: f –коэффициент внутреннего трения грунта.

Рис.4. Схема образования разгружающего свода над кротовой дрены

Рис.5. Схема сил, действующих на половину разгружающего свода

Пролет В – разрушающего свода определяем:

 В = D₁ + 2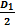 tg(45⁰ - 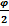) = D₁ [ 1 + tg(45⁰ -  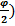]                              (31)

где: D₁ – диаметр полости кротовины; φ – угол внутреннего трения.

         Из условия равновесия получим:

h_c= 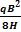 =  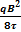=  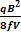=  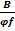                                                 (32)

           Известно, что при формировании кротовин имеем устойчивое равновесие, т.е. исходя из этого:                                                                       H = T – S                                  (33)

           Из уравнений равновесия находим:

h_c= 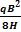 =  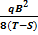                                       (34)

         Из уравнений (30), (32), (33) определяем силу – S:

S = 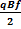 -  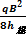                                                   (35)

а приравняв производную 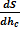  нулю, имеем:

h_c= 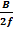                                                   (36)

        Ввиду того, что данное решение применимо для связных грунтов, то коэффициент –  -f  является коэффициентом сопротивления сдвигу, учитывающийся суммарное действие внутреннего трения и сцепления и носит название коэффициент крепости грунта -f_кр :

  f_кр  = f  +                                                                     (37)

где: с – удельное сцепление; 𝛔 – снижающее напряжение, при котором определяется сопротивление связного грунта сдвигу.

Таким образом, конструкцию АД следует оценивать конструкционной прочностью и фильтрационной устойчивостью. При этом устойчивость кротовых дрен  в работе определяются: эффективной плотностью скелета грунта, 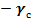; гидродинамическим давлением;  конструкционной прочностью свода кротовой дрены.         

 

Литература:

1.      Аверянов С.Ф. Борьба с засолением орошаемых земель. – М: Колос. 1978. -240с.

2.      Бальчюнас А.И. Кротование минеральных тяжелых почв. – Обзорная информация ЦБНТИ Минводхоза. 1979. -№14. с. 3-76.

3.      Брусиловский Ш.И. Мелиорация минеральных почв тяжелого механического состава. –Минск: Урожай. 1981. –с.159.

4.      Гришков Э.В. О параметрах дренера кротователя. Сб. научных труд. Разработка технологии, рабочих органов машин и орудии для строительства и эксплуатации оросительных систем. 1979. с.62-67.

5.      Гришков Э.В. Устойчивость хода кротователя. Труды ЮжНИИГиМа, вып. 26. Новочеркаск. 1977. с.31-32.

6.      Досжанов О.М. К вопросу исследования рабочего процесса рыхления-кротования минеральных почв //Cб.науч.тр./ ТИИМСХ – Ташкент, 1986.-Вып. 153. -с. 96-99.

7.      Досжанов О.М., *Досжанов Е.О. Эффективность применения рыхлителя-кротователя для регулирования водного режима почвы. (ЮКГУ имени М.Ауезова, г.Шымкент, *Каз НУ имени аль-Фараби, г.Алматы). 2010.

8.      Изергин А.Н. Кротование глинистых и тяжелосуглинистых почв. –Архангельск: Кн. изд-во. 1951. –с. 4-45.

9.      Клейн Г.К. Расчет труб, уложенных в земле. –М.: Госстройиздат. -1957. -194с.