Со школьных уроков информатики нам известна такая дисциплина, как математическая логика [2]. Эта наука (правда, в отрыве от математики) впервые упоминается еще в трудах греческого философа Аристотеля. Своему же формальному описанию математическая логика обязана целой плеяде великих математиков: Готфриду Вильгельму Лейбницу, Джорджу Булю, Фридриху Людвигу Готлобу Фреге, Давиду Гильберту, Джузеппе Пеано и многим другим. Благодаря им была создана классическая истиннозначная логика, в которой каждой умозаключение должно иметь одно из двух значений: «истину» или «ложь». Наиболее широкое применение математическая логика нашла в информационных технологиях и программировании. Конечно же, аппарат данной науки используется и в базах данных. Однако с ними возникла одна проблема. Заключается она в том, что существуют ситуации, когда какой-то атрибут кортежа не содержит какого-либо значения. Например, для некоторых автомобилей оказалось неизвестна их масса. Тогда при занесении информации в базу данных соответствующие поля окажутся пустыми, или, по-другому, масса некоторых автомобилей будет неопределенной, так как известно, что данные автомобили существуют, они, безусловно, обладают массой, но эта масса неизвестна. Именно здесь на передний план выходит трехзначная логика [1], которая оперирует не только значениями «истина» и «ложь», но и значением «неопределенно» или Null-значением. У данной области знаний есть как сторонники, так и противники, которые считают, что неопределенные значения и трехзначная логика являются ошибочными понятиями и что им нет места в четких формальных системах, подобных реляционной модели. Но прежде чем обсуждать плюсы и минусы данной теории, необходимо более подробно разобраться, в чем же заключается проблема отсутствующей информации и что собой представляет трехзначная логика.
В первую очередь, необходимо разобраться в том, какие ограничения накладывает и какие особенности обуславливает использование Null-значений. Очевидно, что, например, если в операции сравнения используется Null-значение, то результат операции будет неопределенным. Тогда вместо таких результатов логических операции, как «true» и «false», будет использоваться новое логическое значение «unknown». По этой причине меняются и таблицы истинности для основных логических операций: дизъюнкции, конъюнкции, а также отрицания. На рисунке 1 представлены данные таблицы истинности вместе с еще одной — таблицей истинности для операции Maybe (может быть), которая используется именно в трехзначной логике.
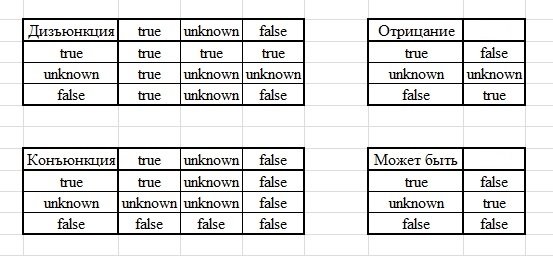
Рис. 1. Таблица истинности для четырех логических операций трехзначной логики
Стоит оговориться, что Null-значение и результат логической операции «unknown» не являются одним и тем же. Так если значение какой-то переменной равно «unknown», то это означает, что значение этой переменной известно и равно оно «unknown», но если значение этой переменной является Null-значением, то это означает, что значение переменной просто не известно.
Null-значения также оказывают влияние на операторы реляционной алгебры [1]. Первые восемь реляционных операций были сформированы Эдгаром Франком Коддом в семидесятых годах прошлого века, и включали в себя следующие: объединение, пересечение, разность, произведение, сокращение, проекцию, соединение и деление. Рассмотрим, что происходит с некоторыми из них. Так на операцию произведения Null-значение не оказывает никакого влияния, а при использовании операции сокращения необходимо возвращать только те кортежи, для которых условие сокращения будет принимать значение «true» (соответственно, не будет принимать значения «unknown» и «false»). Прежде же чем обратить внимание на такие операции, как проекция, объединение, разность и пересечение, необходимо определить, что является дубликатом кортежа в трехзначной логике. Из-за использования неопределенного значения к классическому определению дубликатов (два кортежа считаются дубликатами тогда и только тогда, когда они имеют соответственно одинаковые атрибуты, значения которых соответственно равны) добавляется одна оговорка, что оба значения соответственных атрибутов могут быть Null-значениями. Используя новое определение, все указанные выше операции могут быть выполнены в своем неизменном виде, подразумевая исключение избыточности.
Помимо влияния на операции реляционной алгебры, Null-значения по-особенному ведут себя и при операциях обновлениях. Например, если определенный атрибут некоторой переменной отношения может содержать неопределенное значение, то при попытке вставить в данную переменную отношения с помощью операции «Insert» новый кортеж, не содержащий значения для выбранного определенного атрибута, на место отсутствующего значения системой будет автоматически поставлено неопределенное значение. Если же определенный атрибут некоторой переменной отношения не может содержать неопределенное значение, то при попытке вставить в данную переменную отношения с помощью операции «Insert» или операции «Update» новый кортеж, содержащий неопределенное значение для выбранного определенного атрибута, будет получена ошибка. Также стоит сказать, что при добавлении в некоторую переменную отношения дубликата кортежа (по определению трехзначной логики), обычно будет получена ошибка.
Нельзя не упомянуть про особенности ограничений целостности, связанные с использованием Null-значений [1]. Как известно, ограничения целостности (ограничения, налагаемые на значения, которые разрешено принимать некоторой переменной или комбинации переменных) неформально можно рассматривать как логические выражения, результат вычисления которых не должен быть равен «false». Это означает, что ограничение целостности не будет нарушено даже тогда, когда результат его вычисления будет равен «unknown», хотя точнее будет сказать, что будет неизвестно, нарушено или нет данное ограничение целостности. Однако при работе с ключами ситуация совсем иная. Для первичных ключей должно выполняться правило поддержки целостности сущности (ни один компонент первичного ключа любой базовой переменной отношения не может содержать неопределенные значения), а для внешних ключей — ограничение ссылочной целостности (база данных не должна содержать никаких несогласованных значений внешних ключей).
Несмотря на все вышесказанное, избежать использования трехзначной логики можно, однако это повлечет за собой серьезную избыточность. Рассмотрим пример работы «простой» социальной сети, в которой каждый пользователь заполняет анкету с полями «фамилия», «имя» и «отчество», причем, поле «отчество» можно оставить незаполненным. Каждому пользователю ставится в соответствие некоторый уникальный идентификатор, который согласно описанному выше правилу поддержки целостности сущности не может принимать неопределенное значение, являясь первичным ключом. Очевидно, что наиболее просто использовать в данной ситуации одну переменную отношению, в которой атрибутами будут являться уникальный идентификатор (первичный ключ переменной отношения), фамилия, имя и отчество. Однако, если какой-либо пользователь не заполнит необязательное поле «отчество», то ему будет необходимо назначить Null-значение, то есть воспользоваться трехзначной логикой. Избежать этого можно только за счет уже двух переменных отношения: атрибутами первой будут являться уникальный идентификатор, фамилия и имя, а атрибутами второй — уникальный идентификатор и отчество. Именно так в рассматриваемом примере решается вопрос использования неопределенных значений, но из-за этого появляется избыточность.
В итоге данного обсуждения можно сделать вывод, что хорошо развитый аппарат трехзначной логики скорее является элементом, способным упростить базу данных за счет использования в некоторых местах неопределенных значений, однако использования трехзначной логики можно избежать (хотя при этом и возникает избыточность), и тогда база данных будет частью по-настоящему формальной системы, представляя собой реляционную модель данных.
Литература:
- Дейт, К.Дж. Введение в системы баз данных, 8-е издание.: Пер. с англ. / К.Дж. Дейт. — М.: Издательский дом «Вильямс», 2008. — 1328 с.: ил. — Парал. тит. англ.
- Герасимов, А. С. Курс математической логики и теории вычислимости: учебное пособие, 3-е изд., испр. и доп. / А. С. Герасимов. — СПб.: Издательство «Лема», 2011. — 284 с.







