Динамическая адаптация эвристического алгоритма для задачи транспортной маршрутизации при использовании кросс-докинга



В данной работе подробно рассмотрен один из видов задачи транспортной маршрутизации — при использовании кросс-докинга. В ходе работы рассматриваются различные эвристические алгоритмы, примененные к данному типу задач. Более подробно был изучен и реализован на языке программирования C++ алгоритм итерационного локального поиска и была произведена его динамическая адаптация.

История задачи транспортной маршрутизации начинается со статьи [1], где авторы в 1959 году поставили математическую формулировку и решили задачу о поставке бензина на заправочные станции. На сегодняшний день эта задача является одной из самых известных в области комбинаторной оптимизации.

Общий вид задачи выглядит таким образом: m транспортных средств, первоначально находящихся в депо, должны доставить товар n покупателям. Цель задачи — уменьшить затраты на перевозку товара. Решением классической задачи транспортной маршрутизации является множество маршрутов, которые начинаются и заканчиваются в депо, и удовлетворяют тому условию, что каждый клиент посещается только один раз. Затраты на перевозку могут быть уменьшены за счет оптимизации пройденной дистанции или использования меньшего количества транспорта.

В данной работе исследуется задача, в которой выполняется условие, что склад, через который проходит товар, является кросс-доком. Кросс-докинг — относительно новая стратегия складирования в логистике. Под ним понимают консолидацию товара, поступающего на склад, для упорядочения его для последующих транспортировок. То есть товар, доставленный от поставщиков, перегруппировывают и отправляют прямо к уходящему транспорту без задержки на складе. Загрузка на складе занимает, как правило, менее 24 часов, иногда менее часа. Таким образом, кросс-докинг не только предоставляет покупателям качественное обслуживание, но и дает существенные преимущества по сравнению с традиционным складированием: снижение затрат на хранение, дополнительное пространство на складе, управление стоимостью и циклами обработки заказов. Благодаря этим преимуществам, кросс-докинг широко распространен на практике.

Задача VRPCD формулируется следующим образом. Товар доставляют от поставщиков несколькими одинаковыми транспортными средствами на кросс-док, там товар консолидируют и немедленно отправляют их ритейлерам теми же транспортными средствами. Примеры маршрута и консолидации товара на кросс-доке представлены на рис. 1 и 2 соответственно.

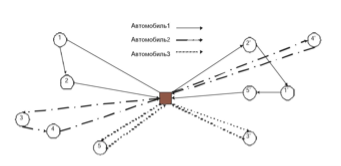
Рис. 1. Пример маршрута

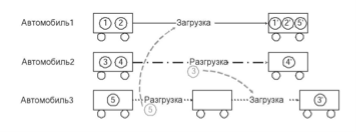
Рис. 2. Пример консолидации товара на кросс-доке

Одним из важных пунктов является одновременное прибытие транспорта на склад. Если же они прибудут не одновременно, некоторым транспортным средствам придется ждать разгрузки и загрузки. Следовательно, время поставок для всего транспорта должно быть синхронизировано, и товар должен быть правильно консолидирован. При правильной организации цепи поставок, товар должен доставляться от поставщика ритейлеру непрерывно, без задержек.

Математическая постановка.

Задача транспортной маршрутизации при использовании кросс-докинга может быть определена как ориентированный граф G = (N, E) с множеством узлов N =P ∪D ∪{0}, где P = {1,…,n} — множество поставщиков, D = {1`,…,n`}, 0 — кросс-док. Пусть E = {(i,j): i, jϵP} ∪ {(i`,j`): i`, j` ϵD} ∪ {(0,i): iϵP} ∪ {(0,i`): i` ϵD} — дуги сети. R = {r₁,…,r_n} — множество запросов, при этом каждый запрос rϵR определен набором {i_r, i`<sub>r</sub>, o<sub>r</sub>}, где i<sub>r</sub> ϵ P, i`_rϵ D, o_r ϵ N — соответствующие спросы. Также пусть V будет множеством одинаковых транспортных средств с ограниченной вместимостью Q для груза. Каждая дуга (i, j) ϵE связана со временем транспортировки t_ij и стоимостью транспортировки c_ij. Каждый узел iϵN связан с временными окнами [a_i, b_i], где a_iи b_i представляют собой минимальное и максимальное время прибытия транспорта в этот узел. Задачей транспортной маршрутизации является нахождение множества S маршрутов для транспортных средств V^S ϵ V с целью минимизации затрат на перевозку с учетом спроса в узлах, временных окон и вместимости транспорта. Маршрут транспортного средства делится на два этапа. Маршрут Pickup начинается на кросс-доке, проходит через поставщиков и заканчивается на кросс-доке. Маршрут Delivery также начинается на кросс-доке, проходит через покупателей и возвращается на кросс-док. Каждый поставщик и покупатель i ϵ{P∪D} посещается только один раз.

Транспортные средства могут оставлять и забирать товар с кросс-дока. Однако этот процесс занимает некоторое время. Если транспорт не меняет товар на кросс-доке, время, проведенное там, равно нулю. В случае если транспорту необходимо разгрузить или загрузить товар, время на кросс-доке считается следующим образом. Пусть A будет постоянное время для подготовки транспортного средства, а B — время для разгрузки или загрузки одной единицы товара. Тогда время t^u_vдля разгрузки товара, привезенного от поставщиков P_v,: t^u_v = A+B_i. Время для загрузки товара для покупателей D_v : t^l_v=A+B _i. Транспортное средство может начать движение от кросс-дока до покупателей только после разгрузки товара, привезенного от поставщиков P_v и после того, как весь товар для покупателей D_v будет загружен. Таким образом, время t^rl_v, когда транспортное средство готово к погрузке товара на кросс-доке: t^rl_v= max(t^a_v+t^u_v, t^fu_v)где t^a_v — время, когда транспорт v прибывает на кросс-док, а t^fu_v — время, когда все транспортные средства, доставляющие товар для дальнейшей транспортировки его транспортом v, заканчивают разгрузку. Тогда время t^d_v, в которое v покидает кросс-док: t^d_v=t^rl_v+t^l_v, и соответственно время, проведенное на кросс-доке равно t^d_v-t^a_v.

Пусть L=L^p∪ L^d, где L^p — множество маршрутов Pickup, L^d — множество маршрутов Delivery. С каждым маршрутом l связана стоимость транспортировки c_q, в нашем случае равная времени транспортировки t_q. Рассмотрим бинарные константы λ_iqϵ {0,1} и δ_i`q`ϵ {0,1}, которые определяют соответственно посещается ли поставщик i ϵ P с запросом r ϵ R в маршруте Pickupl_q ϵ L^pи покупатель i` с запросом r ϵ R в маршруте доставки l<sub>q`</sub> ϵ L^d. Также рассмотрим две бинарные переменные x_q ϵ {0,1} и y_{q`</sub> ϵ {0,1}, чтобы определить, выбраны ли в качестве пути маршруты l<sub>q</sub> и l<sub>q`}. Таким образом, чтобы составить решение задачи, необходимо найти маршруты в L^p и L^d, которые минимизируют функционал

_qx_q+ _{q`</sub>y<sub>q`} → min

с учетом ограничений:

_iqx_q = 1(1)

_i`q`y_q = 1(2)

y_q, x_qϵ {0,1}(3)

Ограничение (1) утверждает, что один маршрут Pickup проходит через поставщика i ϵ P, а ограничение (2), что один маршрут Delivery проходит через покупателя i` ϵ D. Маршруты Pickup и Delivery рассматриваются отдельно друг от друга.

Эвристические алгоритмы решения задачи.

Ранее рассматривалось несколько алгоритмов для решения задачи: в статье [2] TabuSearch, в статье [3] AdaptiveMulti-Restartalgorithm, а в статье [4] Branch-and-Pricealgorithm. В данной работе был использован и реализован на языке C++ алгоритм Iterated Local Search, подробное описание которого можно найти в статье [5].

В таблице 1 представлены результаты работы данного алгоритма для различного количества узлов.

Таблица 1

Результаты реализации алгоритма Iterated local search

η	100	150	200	250	300
f(x)	9514	10973	17963	19750	27350

Динамическая адаптация.

Эвристические алгоритмы дают приемлемое решение задачи в большинстве случаев, но не гарантируют его оптимальность. Это означает, что нарушается принцип оптимальности Беллмана, который утверждает, что «оптимальное решение обладает таким свойством, что независимо от начальных данных и начальной точки, оставшееся решение будет оптимальным, с учетом реализации первой точки» [6]. То есть оптимальное решение сохраняет оптимальность на любых подзадачах. Под временной состоятельностью понимают именно это свойство. С другой стороны, подзадачи имеют меньшую размерность, то есть меньшее пространство поиска, что повышает вероятность нахождения оптимального результата за меньшее время. Таким образом, можно найти лучшее решение, оставаясь в рамках эвристического алгоритма.

Так как решение задач маршрутизации можно представить в виде последовательности точек, которые посещает транспортное средство, то к ним применима оценка временной состоятельности.

Введем следующие обозначения: пусть P — множество тестовых примеров для задачи, p ϵ P — соответственно один пример из этого множества, s(p) — множество решений, полученное при помощи эвристического алгоритма для задачи. Каждое такое решение представляет собой порядок обхода узлов для каждого транспортного средства в течение T периодов, эта величина постоянна. Исходное решение s(p) разделим на части, соответствующие каждому из периодов t = 0, 1,..., T-1. Количество узлов, пройденных в течение первых t периодов, вычисляется по формуле n(t, s(p)) = , где n — количество узлов в тестовой задаче. s⁺(t,p) — часть маршрута s(p), соответствующая порядку обхода узлов после периода t, а s^-(t,p) — до периода t соответственно. Тогда каждое решение можно представить в виде объединения двух частей s(p) = s⁺(t,p) ∪ s^-(t,p).

Рассмотрим текущую задачу p(s^-(t,p)), которая отличается от начальной тестовой тем, что сокращено множество узлов, которые уже входят в часть маршрута s^-(t,p). Через s(p(s^-(t,p))) обозначим решение текущей задачи, найденное при помощи эвристического алгоритма.

Введем определение: решение s(p) называется состоятельным по времени, если для каждого t = 0, 1,..., T-1 верно следующее неравенство

f(s⁺(t,p)) ≤ f(s(p(s^-(t,p))))(4)

где f — целевая функция рассматриваемой задачи.

Для каждого решения s(p) проведем M вычислительных экспериментов, которые состоят в проверке решения на состоятельность по времени. Через b(s(p),t) обозначим число экпериментов, для которых нарушается это свойство после периода t.

Введем определение: экспериментальным уровнем временной состоятельности алгоритма называется величина, определяемая по следующей формуле

con = 1 — 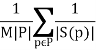Σ_s(p)ϵNΣ_t^T-1b(s(p),t)(5)

где S(p) — множество решений, сгенерированных эвристическим алгоритмом для задачи p.

Заметим, что 0 ≤ con ≤ 1. Чем ближе значение оценки временной состоятельности к 0, тем чаще решение, полученное эвристическим алгоритмом, теряет свойство оптимальности в ходе своей реализации.

Описание работы динамической адаптации.

Метод динамической адаптации алгоритмов для задачи маршрутизации и управления запасами подробно был рассмотрен в статье [7]. Используя его идею, адаптируем его для рассматриваемой в этой работе задачи.

Динамическую адаптацию можно описать следующим образом: на начальном этапе для каждого узла при помощи алгоритма Iterated Local Search генерируется N решений. Из них выбирается то, которое обладает наименьшим значением целевой функции. Каждый маршрут делится на T периодов, после каждого периода задачи расссматривается новый этап, но уже с меньшим количеством узлов для каждого транспорта. На каждом этапе снова запускается эвристический алгоритм. Если на новом этапе удается найти лучшее решение, то маршрут меняется. Улучшения эвристического алгоритма таким способом возможны из-за уменьшения количества рассматриваемых узлов на каждом этапе.

Применение динамической адаптации.

В среднем, маршрут для каждого транспортного средства, сгенерированный при помощи алгоритма Iterated Local Search, состоит из 3–5 узлов. Следовательно для проведения эксперимента возьмем параметр T = 3. В качестве всего множества задач P рассмотрим одну задачу с различным количеством узлов, т. е. |P| = 5. Для каждой тестовой задачи сгенерируем по 10 решений, количество тестов M для одного решения s(p) равно 5.

По результатам экспериментов был найден средний экспериментальный уровень временной состоятельности для алгоритма Iterated Local Search: conILS=0.385, что означает, что чуть больше трети решений, сгенерированных на начальном этапе, сохраняют свойство оптимальности в процессе своей реализации, т. е. существуют другие маршруты, которые можно получить при помощи динамической адаптации, значение целевой функции которых будет меньше по сравнению с начальным решением. В таблице 2 представлены результаты динамической адаптации алгоритма Iterated Local Search для задач с различным количеством узлов при T=3.

Таблица 2

Результаты реализации динамической адаптации алгоритма

Η	100	150	200	250	300
f(x)	9514	10908	17640	19118	26146

При анализе данных из таблиц 1 и 2 можно заметить, что в большей части случаев динамический алгоритм показал лучшие значения. В примерах малой размерности полученное эвристическим алгоритмом решение уже является оптимальным или близким к оптимальному, поэтому получить улучшение не удалось. Улучшение решения при помощи динамической адаптации по сравнению с эвристическим алгоритмом находится в пределах 0–4,4 %.

Заключение.

В данной работе был исследован один из видов задачи транспортной маршрутизации — при использовании кросс-докинга. Среди нескольких, примененных ранее к этому типу задач, алгоритмов был выбран алгоритм Iterated Local Search, который был реализован на языке C++ и рассмотрен на тестовых данных. Была произведена оценка уровня временной состоятельности алгоритма, среднее значение данной величины равно 0,385, что означает, что эвристика не дает оптимального решения. Также был разработан метод динамической адаптации алгоритма. Улучшение значения решения в экспериментах для задачи с различным количеством узлов принимает до 4.4 %. Результаты показали, что использование на практике алгоритма динамической адаптации позволяет генерировать маршруты меньшей длины, и, соответственно, меньшие по времени.

Литература:

1. Dantzig G. B., Ramser J. H., The Truck Dispatching Problem, 1959.
2. Wen M., Larsen J., Clausen J., Cordeau J.-F., Laporte G., Vehicle routing with cross-docking // Journal of The Operational Research Society, 2009.
3. Tarantilis C. D. Adaptive multi-restart Tabu Search algorithm for the vehicle routing problem with cross-docking, 2012.
4. Santos F. A., Mateus G. R., Salles da Cunha A. A Branch-and-price algorithm for a Vehicle Routing Problem with Cross-Docking // Electronic Notes in Discrete Mathematics, 2011.
5. Morais V., Mateus G., Noronha T. Iterated local search heuristics for the Vehicle Routing Problem with Cross-Docking // Expert Systems with Applications, 2014.
6. Беллман Р. Динамическое программирование. М.: Изд-во иностранной литературы, 1960. 400 с.
7. Shirokikh V. A., Zakharov V. V. Dynamic Adaptive Large Neighborhood Search for Inventory Routing Problem. // Advances in Intelligent Systems and Computing, Vol. 359, 2015.