Идентификация и аутентификация пользователей для автоматизированных систем высших учебных заведений



Article is devoted to the organization of user identification and authentication in the automated system of the university. It is shown that the results achieved to date in addressing the challenges of data mining user identification and authentication, do not provide the required level of network security in general. As a basic solution of the problem analysis of multiple subjects and objects used fuzzy logic. Used evaluation function separability and compactness, as well as optimized Maximin method. In this paper we present an algorithm for clustering uncertain objects and subjects.

Keywords: identification and authentication of users, clustering, fuzzy sets, fuzzy relational data model, the membership function

В настоящее время затруднение применения методов анализа данных характеризуется тем, что конкретная задача из выбранной предметной области, а именно выборка данных, в рамках данной задачи, характеризуется не только числовым характером атрибутов, но и мерой неопределенности. Если рассмотреть области макроэкономических, социологических, маркетинговых, медицинских, то при анализе в большинстве случаев без лингвистической формы представления данных задача построения математической модели становиться крайне трудоемкой задачей [1]. Оперирование подобными данными предоставляет необходимость организации хранения нечетких переменных и их функций принадлежности. А применяя данный подход при решении задач идентификации и аутентификации пользователей (ИАП) необходимость хранить множества субъектов и объектов [2]. На текущий момент представлен небольшой ряд разработок, позволяющих управлять хранилищами данных с нечеткими переменными и их функциями принадлежности. Взаимодействие субъектов и объектов представлено на рисунке 1.

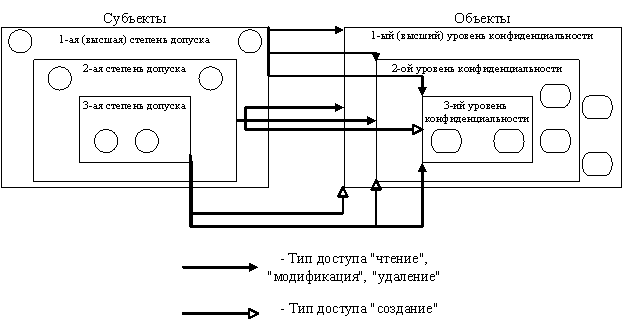Рис. 1. Взаимодействие субъектов и объектов

Результаты, достигнутые в задачах ИАП с использованием интеллектуального анализа данных, не дают полной защищенности сети в целом, и на текущий момент остается ряд нерешенных задач, а именно использование нечетких множеств субъектов и объектов не поддержано разработанными методами анализа.

В задаче ИАП исследуемая совокупность множеств субъектов и объектов (МСО) представляет собой в любой сети некоторое конечное множество элементов , которое в целях решения задачи будет являться некоторым множеством объектов кластеризации. Определим конечное множество признаков или атрибутов , каждый элемент которого количественно представляет свойство, или характеристику элементов МСО. Здесь — общее количество элементов МСО, —общее количество измеримых признаков [3].

Измерение признаков множества в общем случае не является трудоемкой задачей и привязано к определенной компьютерной сети (КС), таким образом, все признаки множества можно представить в некоторой количественной шкале. Это представление позволяет каждому элементу множества поставить в соответствие вектор , где — некоторое количественное значение признака для множества [1].

В целях определенности положим, что любой принимает действительное значение. Каждый вектор значений признаков представим в виде матрицы , размерность которой , а каждая строка которой равна значениям вектора , данная матрица имеет прямоугольный вид, в некоторых случаях при определении каждому элементу одного признака матрица будет квадратной.

Используем для решения задачи анализа МСО нечеткий кластерный анализ [4].

Формулирование задачи нечеткого кластерного (НК) анализа определяется следующим образом: на основе исходных данных матрицы устанавливается некоторое нечеткое разбиение , или некоторое нечеткое покрытие МСО на число нечетких кластеров , где , а нечеткое разбиение (покрытие) определяет экстремум целевой функции в нечетких разбиениях или экстремум целевой функции в нечетких покрытиях [5].

Уточнение вида целевой функции и типов искомых нечетких кластеров требуется для решения задачи МСО в каждой КС (определение нечеткого разбиения или покрытия).

Определим нечеткую реляционную модель данных, а также требование и ограничение модели [6].

Схема отношения является конечным множеством имен атрибутов . Для каждого имени атрибута сопоставляется множество , данное множество будет является доменом атрибута , . Пусть каждый домен будет представлен произвольным непустым конечным или счетным множеством, а также .

При определении задачи МСО необходимо ввести нечеткие домены реляционных отношений, для этого дополнительно вводятся имена атрибутов , универсальное множество , а также терминальное множество значений (в общем случае — нечеткие метки).

Нечеткое отношение представляет собой конечное множество отображений из в , для этого необходимо, чтобы хотя бы одно , где — нечеткий домен.

В данном случае такая модель представления ориентирована на представление нечетких чисел, а в нашем случае это и есть нечеткие МСО. Следовательно, домен атрибута нечеткого числа является множеством действительных чисел. Определение нечетких чисел основано на таких показателях, как функция принадлежности и лингвистическая оценка. Лингвистической оценкой называется одно из возможных значений лингвистической переменной, при определении соответствующих термов [7].

В целях эффективной кластеризации используются следующие действия:

Используется функция оценки сепарабельности и компактности, где функция сепарабельности — функция, при применении нескольких переменных которой имеется возможность разделения влияния аргументов на общий результат (при использовании МСО некоторые объекты или субъекты должны быть выделены); функция компактности — функция реализации одного и того же образа, отражающаяся в признаковом пространстве в геометрически близкие точки и образующиеся скомпонованные сгустки (при использовании МСО некоторые объекты и субъекты могут быть объединены в единые группы).

Для обеспечения максимальной кластеризации МСО необходимо выполнить следующую последовательность действий:

1. Произведем инициализацию разбиений с использованием метода, тогда разделение объектов будет настолько максимально, насколько это возможно.
2. Применяя методы оптимизации, находим локальный оптимум.
3. Переходим на следующую итерацию.

Данная последовательность действий выполняется до его сходимости, обеспечивая максимальную кластеризацию МСО.

Данный подход позволяет найти оптимальное решение для количества кластеров , с помощью алгоритма объединения находим разбиение .

Используя оптимизированный максиминный метод в сочетании со стратегией слияния, всегда можно сформировать оптимальные варианты для переменного количества кластеров [1].

С помощью функций оценки, которые основаны на мерах сепарабельности и компактности, выбираем оптимальный вариант кластеризации.

Алгоритм нечеткой кластеризации:

Вход: множество данных .

Шаг 1. , , где — максимальное количество кластеров. Выберем случайным образом объект в качестве точки старта . Выполним многошаговый максиминный алгоритм с параметрами , производя поиск оптимального множества кластеров для . Вычислим функцию оценки для , состоящую выполнении двух последовательных действий. Сначала обеспечиваем слияние значений одного класса кластеров, а затем — разделение разных классов (использование слияния объектов и субъектов одной группы и разбиение групп обеспечивает возможность применения данного алгоритма для МСО).

Шаг 2. Выполним алгоритм слияния, получая множество кластеров , выберем центр , в качестве точки старта , , . Выполним многошаговый максиминный алгоритм с параметрами для поиска оптимального множества кластеров для индекса . Вычислим функцию оценки для и обозначим как . Если , тогда , , . Повторяем шага 2, пока не будет.Вывод: — оптимальное множество кластеров.

Выход: оптимальное множество кластеров .

2 Этап имеет ряд преимуществ перед другими алгоритмами кластеризации.

В целях проверки данного алгоритма на КС проведен опрос администраторов о множествах субъектов и объектов. Для анализа использовались такие разделы, как защищенность объектов, общие данные по объектам и субъектам, уровень активности субъектов, возможность перемещения объектов, возможность доступа к объектам из глобальной сети, уровень ответственности субъекта за присвоенные ему объект и т. д.

Основной целью данного опроса являлось изучение уровня субъектов и уровня секретности объектов. Такие данные необходимы для управления администраторами сетью, разработки мер, направленных на повышение защиты информации в целях компьютерной безопасности.

На большинство вопросов нельзя дать ответы, которые могут быть выражены в точной количественной мере, например: «Как часто на объекте появляется финансовая информация по организации?». Варианты ответов: часто, редко, никогда. Кластеризация в таком случае является трудоемкой задачей, так как на классы делятся различные лингвистические переменные. А для анализа необходимо соответствие меткам функций принадлежности для пригодности обработки информации.

Для проверки были использованы данные Московского государственного университета приборостроения и информатики, данные приведены в табл. 1.

Таблица 1

Функции принадлежности объектов

Имя переменной	Класс объекта	Функция принадлежности
Уровень доступности	Высший	0,3
Уровень доступности	Средний	0,8
Уровень доступности	Минимальный	0,5
Класс объекта	Наивысший	0,2
Класс объекта	Средний	0,4
Класс объекта	Низший	0,8

Результат кластеризации объектов представлен на рис. 2.

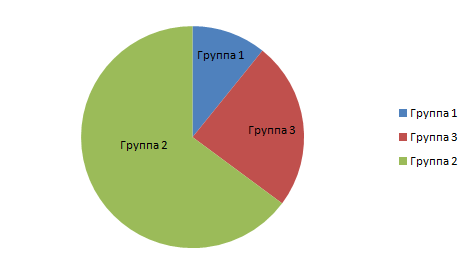
Рис. 2. Кластеризация объектов

Анализ кластеризации объектов показал, что в рамках университета наиболее выделяется класс объектов среднего уровня доступности и низший класс, чаще всего такие объекты — это общедоступные лабораторные работы для студентов и т. д. Данные по анализу субъектов приведены в табл. 2.

Таблица 2

Функции принадлежности субъектов

Имя переменной	Класс объекта	Функция принадлежности
Уровень активности	Высший	0,8
Уровень активности	Средний	0,4
Уровень активности	Минимальный	0,2
Класс субъекта	Наивысший	0,8
Класс субъекта	Средний	0,4
Класс субъекта	Низший	0,2

Результат кластеризации субъектов представлен на рис. 3.

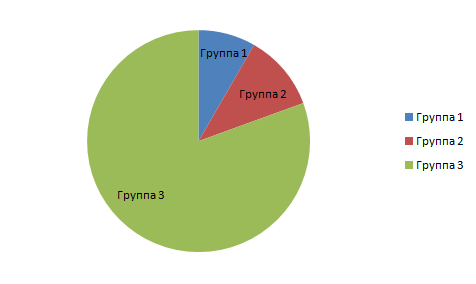
Рис. 3. Кластеризация субъектов

Результаты анализа показаны на основе выделения кластера, представители которого являются преподавателями университета. Стоит отметить, что преподаватели часто работают дома, причем общая активность из-за этого не падает.

Подавляющее большинство активных субъектов — являются студентами, а объекты — диски общего доступа с выложенными (и выкладываемыми) на них лабораторными (домашними) работами.

Использование математического аппарата, позволяющего провести анализ МСО позволяет выполнить программную реализацию программного продукта, позволяющего проводить анализ любой КС [4]. Стоит отметить, что опрос экспертов возможен на любом количестве и составе вопросов. Алгоритм кластеризации позволил провести группировку распределенных данных.

Литература:

1. Сумкин К. С.Модель разграничения прав доступа и программная реализация модели для компьютерных сетей / Диссертация на соискания ученой степени кандидата технических наук. М.: МГУПИ. 2009.
2. IFSA'97. Prague. Seventh International Fuzzy System Association World Congress. University of Economics Prague. Fuzzy Neural Networks. Tutorium, IFSA’97, Prague, 1997. 37 pp.
3. Tatra Mountaints. Mathematical Publications / Bratislava. Mathematical Institute Slovak Academy of Sciences, Vol. 13, 1997.
4. Eufit'98 6th European Congress on Intelligent Techniques and Soft Computing ELITE — European Laboratory for Intelligent Techniques Engineering. Hrsg. Von Prof. Dr. Dr. h. c. Hans-Jurgen Zimmermann. — Aachen: Mainz, 1998 ISBN3–89653–500–5. Munich 2013. p. 23–26.
5. Горбоконенко Е. А., Ярушкина Н. Г.Представление нечеткой информации в СУБД / Труды 7-ой национальной конференции по искусственному интеллекту. М.: Физматлит. 2000. С. 479–484.
6. Горбоконенко Е. А., Ярушкина Н. Г.Применение нечеткой СУБД в САПР / Труды конгресса «Искусственный интеллект в XXI веке. Научное издание. М.: Физматлит. 2001. С. 142–149.
7. Городецкий В. И.Современное состояние технологии извлечения знаний из баз и хранилищ данных. Часть 1 / Новости ИИ. 2002. № 3. С. 36–39.