Расчет оптимального плана распределения грузопотоков между морскими портами



Расчет оптимального плана распределения грузопотоков между морскими портами

Бабаян Петр Дмитриевич, кандидат технических наук, доцент;

Горелова Оксана Владимировна, старший преподаватель

Национальный университет «Одесская морская академия» (Украина)

Рассмотрена методология выполнения расчетов оптимального распределения грузопотоков между морскими портами при внутренних и международных перевозках. Изложены особенности решения линейной транспортной задачи применительно к перевозкам через морские порты.

Ключевые слова: грузопотоки, морские порты, экспорт, оптимизация

В век стремительного развития и внедрения компьютерной техники для решения различных практических задач, используются компьютерные технологии. Эта возможность обеспечивается развитием и внедрением мощного потока программного обеспечения. В том числе и для решения одной из самых сложных задач — задачи транспортировки груза между портами корреспондентами с минимальными материальными и временными затратами [1]. Вследствие того, что огромное количество возможных вариантов перевозок груза затрудняет получение самого экономичного плана практическим или экспертным путем, то появилась необходимость в разработке специального алгоритма, который позволяет быстро решать подобные задачи. Большой экономический эффект при планировании грузоперевозок дает применение математических методов линейного программирования. С помощью MSExcel можно решать различные экономические задачи, в том числе и транспортные задачи.

Для разработки и построения оптимальных планов распределения грузопотоков с помощью современных информационных технологий специалистами по транспортной логистике, менеджерами (операторами судоходных компаний — фрахтовыми брокерами, транспортными агентами и ассистентами грузоперевозчиков, с одной стороны, и экспедиторами — ассистентами грузовладельцев от имени грузополучателей и грузоотправителей, с другой стороны) требуется специальная подготовка [2, 3]. В современных сложных экономических условиях снижение совокупных транспортных расходов является важным фактором конкурентоспособности национальной продукции на внешних рынках [4, 5]. С другой стороны, для морских портов это является основой сохранения их конкурентных позиций на морских бассейнах [6,7,8]. В условиях разразившегося мирового экономического кризиса и замедления экономического роста отмеченные задачи приобрели особую актуальность [9,10].

Ввиду этого, возникает потребность решения транспортной задачи по оптимальному распределению грузопотоков между портами для основных позиций экспортной номенклатуры, как-то по зерну, лому, чугуну, стальному прокату и прочим экспортным грузам [11,12, 13].

Рассмотрим пример составления оптимального плана морских грузоперевозок между портами корреспондентами: портами — отправителями и портами — получателями. Данная транспортная задача решается с использованием методов линейного программирования с целью минимизации суммарных расходов на морскую перевозку определенного рода груза, заданного количества груза от портов — грузоотправителей к портам — грузополучателям.

Для четырех грузополучателей, находящихся в портах — назначения: Мерсин, Стамбул, Трабзон, Сфакс требуется поставить зерно — ячмень, который заготовлен и находится в трех портах — отправителях Черноморско–Азовского бассейна: Октябрьск, Усть — Дунайск и Мариуполь у грузопоставщиков.

Каждый из портов — отправителей может поставить соответственно 60, 50 и 110 тыс. т ячменя (предложение поставщиков — грузоотправителей). Потребности в ячмене грузополучателей, находящихся в портах — назначения составляют соответственно 40, 30, 95 и 55 тыс. т. Сумма объемов отправляемого ячменя в тыс. т из трех разных портов равна сумме объемов получаемого ячменя в тыс. т в четырех портах-получателях (назначения). Тарифы или фрахтовые ставки на перевозку одной тонны ячменя от каждого из портов отправления к каждому из портов назначения задаются матрицей транспортных расходов — ставками фрахта С в целых числах и имеют размерность долл. на 1 тонну.

.

В левом верхнем углу произвольной (i,j) клетки стоит коэффициент затрат (ставка фрахта) — затраты на перевозку единицы груза от i –го порта — отправителя (поставщика) к j — му порту — получателю (потребителю).

Постановка задача формулируется следующим образом: найти объемы перевозок для каждой пары «поставщик — потребитель» так, чтобы объемы поставок от всех портов –отправителей (поставщиков) были реализованы, и спросы всех заявок и соответственно поступлений груза в порты — потребителей (получателей) были удовлетворены, при этом суммарные фрахтовые затраты на перевозку ячменя были минимальны.

Обозначим через x_ij объем перевозки от i — го порта — поставщика к j — му порту — потребителю. При этом заданные объемы предложения грузоотправителей из портов — поставщиков и заданные объемы спроса грузополучателей в портах назначения накладывают ограничения на значения неизвестных x_ij.

1. Чтобы объем-мощность исходящего потока груза от каждого из поставщиков (портов — отправителей) была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок:

.

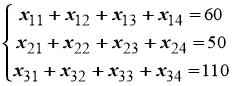2. Аналогично, чтобы объем-спрос каждого из потребителей в портах назначения был удовлетворен, подобные уравнения баланса составляются для каждого столбца таблицы поставок:

.

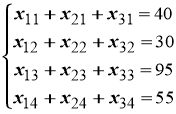3. Очевидно, что объем перевозимого груза от каждого конкретного порта — отправителя к каждому конкретному порту — получателю не может быть отрицательным, поэтому следует ввести ограничение не отрицательности переменных:

x_ij ≥ 0.

4. Объем перевозимого груза от каждого конкретного порта — отправителя к каждому конкретному порту — получателю должен выражаться целым числом.

Суммарные затраты F (суммарный фрахт за морскую перевозку) выражаются через коэффициенты затрат, взятых из матрицы С, существующих фрахтовых ставок, следующим образом:

Для математической постановки транспортной задачи в общем виде обозначим через с_ij коэффициенты затрат, через M_i — суммарные объемы отправок груза от портов — поставщиков, через N_j — суммарные объемы получения грузов потребителями в портах назначения, где i=1,2,…,m, j=1,2,…,n, m — число портов — поставщиков, n — число портов — потребителей.

Тогда система ограничений примет вид:

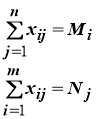. (1)

Система (1) включает в себя уравнения баланса по строкам и по столбцам.

При этом суммарные объемы отправок грузов из портов — поставщиков равны суммарным объемам поставок грузов в порты — назначения потребителям, т. е.

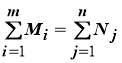
Целевая функция в данном случае приобретает вид:

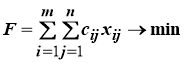(2)

Таким образом, решение задачи заключается в поиске из множества неотрицательных решений системы ограничений (1) найти такое решение, при котором значение целевой функции (2) было минимальным.

Рабочий лист EXCEL с введенными исходными данными для решения данной транспортной задачи имеет вид (рис 1):

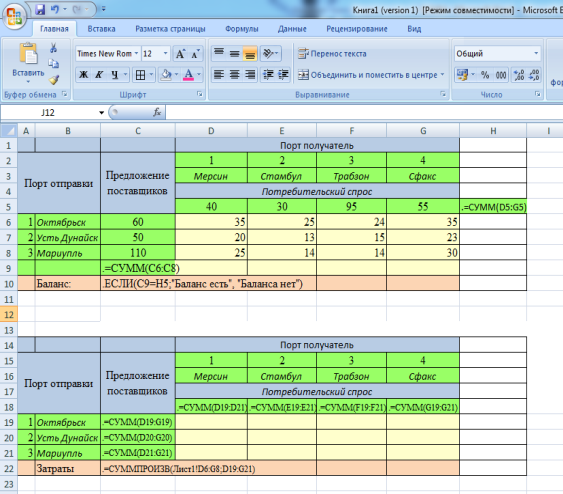
Рис. 1.

Затем настраиваем программу «Поиск решения» как показано на рис. 2

В появившемся окне «Поиск решения» установите курсор на кнопку «Выполнить» и щелкните левой клавишей мыши.

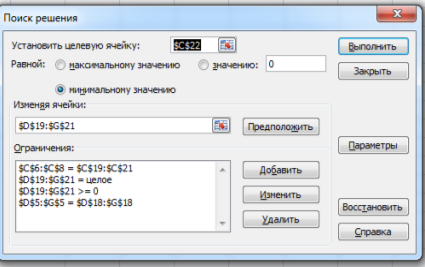
Рис. 2.

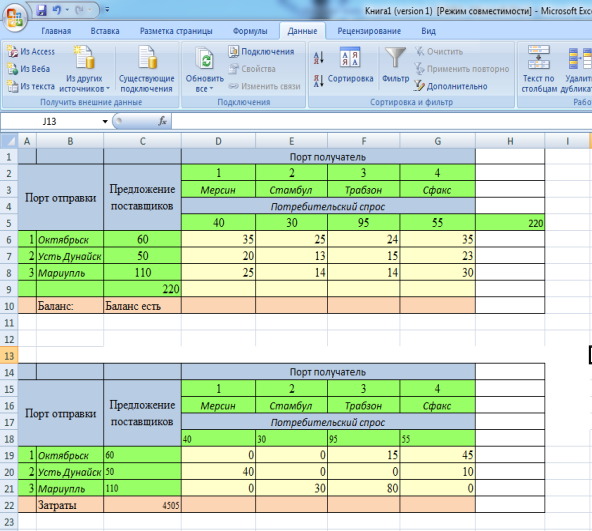
Рис. 3.

После того как на рабочем листе появилось решение (рис.3) в появившемся диалоговом окне «Результаты поиска решения» (рис.4) установите курсор на переключатель «Сохранить найденное решение» и щелкните левой клавишей мыши. Для завершения расчетов щелкните на кнопке ОК.

Рис. 4.

Таким образом, найдено решение рассматриваемого примера транспортной задачи по перевозке ячменя на экспорт из портов Черноморско –Азовского бассейна. Оптимизация распределения грузопотока между морскими портами в форме линейной транспортной задачи эффективна как для обеспечения своевременной доставки внешнеторговых грузов, так и внутренних (каботажных) морских перевозках [14,15].

Методы оптимизации применяются во всех отраслях социально — экономической жизнедеятельности современного общества, принося существенную экономическую выгоду и предупреждая финансовые крахи. Они позволяют принимать разнообразные управленческие решения в условиях риска и неопределенности. Уже при помощи более мощных программных комплексов, работающих на основе генетических алгоритмов, нечеткой логики и нейронных сетей.

Литература:

1. Крутоног Л. Г. Аспекты формирования интегрированных логистических систем при организации внешнеторговых перевозок. Практика и тенденции // Транспорт: наука, техника, управление. 2015. № 5. С. 57–59.
2. Елисеев С. Ю., Тучков Э. В., Куренков П. В. Логистика в управлении внешнеторговыми перевозками // Экономика железных дорог. 2005. № 7. С. 28.
3. Гагарский Э. А., Кириченко С. А. Интермодальные перевозки и их операторы // Логистика. 2002. № 1. С. 20.
4. Кириченко С. А. Экспорт металлов, проблемы и перспективы транспортного обеспечения // Национальная металлургия. 2002. № 2. С. 53.
5. Кириченко И. С., Бабаян П. Д. Тенденции экспорта лома черных металлов из РФ // Вторичные металлы. 2015. № 5–6. С. 50.
6. Чимшир В. И., Чимшир А. В. Основные аспекты формирования организационно-экономического механизма обеспечения конкурентоспособности морского порта // Восточно-Европейский журнал передовых технологий. 2014. Т. 2. № 3 (68). С. 21–25.
7. Гагарский Э. А. Логистические транспортно-технические системы -основы развития транспорта // Морской флот. 2001. № 6. С. 30.
8. Гагарский Э. А., Кириченко С. А., Козлов С. Г. Стратегические направления развития морских портов России// Бюллетень транспортной информации. 2016. № 4 (250). С. 3–10.
9. Лысенко Н. С. Особенности формирования результатов морского транспорта при замедлении экономического роста // Вiсник Хмельницького нацiонального унiвер-ситету. Економiчнi науки. 2014. Т. 2. № 2 (210). С. 191–194.
10. Гагарский Э. А. Прогрессивные транспортно-технологические системы: трудности роста // Морской флот. 2009. № 3. С. 3.
11. Кириченко И. С., Лернер В. К., Сипаро К. А. Тенденции экспорта российского чугуна // Молодой ученый. 2015. № 23 (103). С. 155–160.
12. Кириченко А. С., Сипаро К. А., Букин А. В. Экспорт черного лома и проблемы обеспечения морских перевозок // Вторичные металлы. 2014. № 5. С. 20.
13. Сипаро К. А., Лернер В. К. Развитие грузопотоков российского зерна в направлении морских портов // Молодой ученый. 2014. № 3 (62). С. 349–353.
14. Кириченко И. С. Экспорт лома в I полугодии // Вторичные металлы. 2012. № 5. С. 38.
15. Кириченко И. С., Алексахин А. В., Бабаян П. Д. Особенности и проблемы заготовки и транспортировки металлолома Арктики // Молодой ученый. 2016. № 1. С. 160–165.