Учет влияния длительности действия нагрузки ивязкости битума на величину модуля упругости асфальтобетона
Евдокимов Александр Владимирович, студент
Сибирская государственная автомобильно-дорожная академия
В статье кратко описаны методики расчета асфальтобетонных покрытий, в которых модуль упругости применяется в качестве параметра материала для расчета деформаций, мер теории накапливания повреждений. Предложено ввести в математические модели, учитывающие влияние на модуль упругости продолжительности действия нагрузки и вязкости битума, классические формулы расчета вязкости.
Ключевые слова: асфальтобетонное покрытие, вязкость, длительность нагрузки
Асфальтобетонные покрытия и основания получили широкое распространение в практике строительства дорог. Конструкции с такими покрытиями и основаниями относят к нежестким дорожным одеждам, которые конструируют и рассчитывают в соответствии с требованиями [1]. Одним из применяемых в этом документе критериев расчета дорожной конструкции является ее проверка по допускаемому упругому прогибу. Решение задачи о прогибе дорожной одежды, применяемое в нормативе [1], получено М. Б. Корсунским [2, 3]. Решение М. Б. Корсунского базируется на анализе работ предшественников Д. Бурмистра [4, 5], И. И. Иванова [3, 6], Б. И. Когана [7] и др. специалистов и преследует цель устранения недостатков этих работ. Базовым решением является задача Д. Бурмистра, которая в последствие решалась К. Юшитой [8], Ю. Хуангом [9], Д. Миловичем [10] даны для других граничных и краевых условий. По мере развития применения теории упругости к решению задачи о напряженно-деформированном состоянии (НДС) дорожной конструкции сложность метаматематических выкладок возрастала, что привело к применению приближенных методов строительной механики и разработке различных программных продуктов. Для инженерных расчетов применяются формулы, являющиеся решением задачи о прогибе дорожной одежды относительно общего модуля упругости слоистой среды. Автор приведет некоторые из таких формул. А. Я. Тулаев [11] приводит формулу Е. Барбера, аппроксимирующую решение Д. Бурмистра, и позволяющую вычислить модуль упругости на поверхности двухслойной системы:
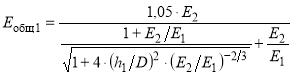 (1)
(1)
Где E1 и Е2 — модули упругости материалов верхнего и нижнего слоев, в случае если подстилающий слой является слоистым полупространством, то Е2 может быть найден, как общий модуль упругости, Па; h1 — толщина верхнего слоя двухслойной системы.
Согласно решению Н. Н. Иванова (метод Союздорнии) общий модуль упругости находят по формуле [3, 12]:
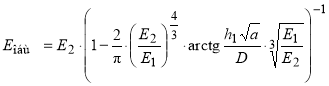 (2)
(2)
Согласно решению М. Б. Корсунского, применяемому в нормативе [1] общий модуль упругости определяют по формуле:
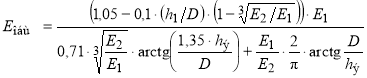 (3)
(3)
Где hэ — эквивалентная толщина.
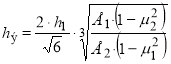 (4)
(4)
Из анализа представленных формул следует, что достоверное прогнозирование модуля упругости материала слоя Е1, например асфальтобетона, обуславливает точность всего расчета. Таким образом, математическое моделирование зависимости модуля упругости асфальтобетона от различных факторов является важной и неотъемлемой задачей расчета дорожной одежды по допустимому упругому прогибу.
Другим направлением приложения этой задачи являются появившиеся в последнее время модифицированные критерии прочности и условия пластичности асфальтобетона [13–15], в которых одним из параметров материала являются меры теории накапливания повреждений, сплошность или поврежденность. В этих методах поврежденность может определяться через отношение модулей упругости асфальтобетона, вычисленных по результатам испытаний на воздействие повторных и однократной нагрузок [15–19]. Кроме того, модуль упругости асфальтобетона может быть применен в расчетах дорожных одежд по критерию упруго пластической деформации. В этом случае найденные через модуль упругости обратимые деформации суммируются с пластическими, которые можно вычислить по формулам, опубликованным в работах [20, 21]. Величина модуля упругости асфальтобетона необходима для определения давлений, передаваемых асфальтобетонными слоями дорожной одежды на их основание [22]. Такой расчет является важным потому, что величина этого давления обуславливает точность расчета главных напряжений в основаниях и грунтах, который может выполняться по традиционным способам [23, 24] или по одной из современных модифицированных моделей [25–30]. Модифицированные модели расчета главных и касательных напряжений позволяют рассчитывать грунты и дискретные материалы по сопротивлению сдвигу, которое может обеспечиваться критерием расчета по безопасным давлениям [31–35], в основе которого возможно использование оригинального критерия Кулона — Мора или его различных модификаций [36–39].
Таким образом, модуль упругости асфальтобетона является параметром расчета самого асфальтобетона в покрытия и основаниях, а так же расчетов других элементов дорожных конструкций. В первом случае модуль упругости асфальтобетона позволяет вычислить деформации этого материала и перемещение покрытия и основания, а втором случае без него нельзя обойтись при расчете давлений, передаваемых пакетом асфальтобетонных слоев на нижележащую часть конструкции.
Одной из современных математических моделей, раскрывающих зависимость модуля упругости асфальтобетона от продолжительности воздействия нагрузки, является аналитическое решение, изложенное в статье [40]. Согласно этому решению модуль упругости вычисляют по формуле:
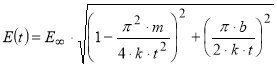 (5)
(5)
Где t — продолжительность воздействия нагрузки, с; Е — конечная величина модуля упругости при t=, МПа; k — модуль жесткости асфальтобетона, МН/м; b — коэффициент, учитывающий вязкие свойства среды, МНс/м.
При продолжительности действия нагрузки больше 10–5 с, формула (5) приводится к виду:
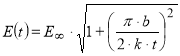 (6)
(6)
Авторы работы [40] указывают, что коэффициент b эквивалентен вязкости среды, то есть b. Такая эквивалентность позволяет использовать в выражениях (5) и (6) различные формулы для определения вязкости. Известны различные формулы для определения вязкости асфальтобетона, грунтов и жидкостей, которые приведены в работе [41], а некоторые из них представлены нами в табл. 1.
Задачей наших последующих исследований является обоснование модели расчета вязкости для ее применения в формулах (5) и (6). Для этого выполняются экспериментальные работы, в ходе которых определяем вязкость и модуль упругости асфальтобетона.
Таблица 1
Формулы для расчета вязкости материалов ижидкостей [41]
|
Автор |
Формула |
|
А. М. Богуславский |
|
|
где z — вертикальное напряжение; z — скорость деформации; т — коэффициент |
|
|
Н. Н. Маслов |
|
|
где к и н — соответственно конечное и начальное значения динамической вязкости грунта при сдвиге, Пас; n — параметр |
|
|
Бьюсмана |
|
|
где а и b — параметры, определяемые по кривой t=f(t) |
|
|
Пуазейль |
|
|
где 0 — вязкость воды при t=0; t — температура, о С; a, b, c — коэффициенты для каждой жидкости |
|
|
Слотт |
|
|
где a, с, п — постоянные, определяемые для каждой жидкости |
Литература:
1. ОДН 218.046–01. Проектирование нежестких дорожных одежд. – М.: ГСДХ Минтранса России, 2001. — 146 с.
2. Корсунский М. Б. Напряженно-деформированное состояние дорожных одежд с учетом модуля сцепления слоев / М. Б. Корсунский // Материалы всесоюзной межвузовской научно-технической конференции по прочности дорожных одежд. — Харьков: 1968. — С. 39–44.
3. Конструирование и расчет нежестких дорожных одежд / Н. Н. Иванов и др. — М.: Транспорт, 1973. — 328 с.
4. Burmister D. M. The Theory of Stresses and Displacements in Layered Systems and Applications to the Design of Airport Runways // Proceedings, Highway Research Board. — 1943. –Vol. 23. — P. 126–144.
5. Burmister D. M. Stress and Displacement Characteristics of a Two-Layered Rigid Base Soil System: Influence Diagrams and Practical Applications. // Proceedings Highway Research Board. — 1956. — Vol. 35. — P. 773–814.
6. Иванов Н. Н. Проектирование дорожных одежд / Н. Н. Иванов и др. — М.: Изд-во автотранспортной литературы, 1955. — 250 с.
7. Коган Б. И. Напряжения и деформации двухслойных и многослойных покрытий: автореф. д-ра. техн. наук / Б. И. Коган– Харьков: Изд-во ХГУ, 1958. — 32 с.
8. Ueshita K., Meyerhof G. G. Surface Displacement of an Elastic Layer under Uniformly Distributed Loads // Highway Reasearch Board Record. — 1968. — No. 228. — P. 1–10.
9. Huang Y. H. Computation of Equivalent Single-wheel Loads Using Layered Theory // Proceedings, Highway Research Board. 1969.
10. Milovic D. Stress and Displacements for Shallow Foundations. // Elsevier Science Publisher, Amsterdam. The Netherlands. 1992.
11. Тулаев А. Я. Проектирование оптимальных нежестких дорожных одежд / А. Я. Тулаев и др. — М.: Транспорт, 1977. — 117 с.
12. Иванов Н. Н. Расчет и испытание нежестких дорожных одежд / Н. Н. Иванов, М.: Высшая школа, 1971. — 100 с.
13. Александрова Н. П., Александров А. С., Чусов В. В. Учет поврежденности структуры асфальтобетона в критериях прочности и условиях пластичности // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 219–225.
14. Александрова Н. П., Александров А. С., Чусов В. В. Модификация критериев прочности и условий пластичности при расчетах дорожных одежд // Вестник Сибирской государственной автомобильно-дорожной академии. — 2015. № 1 (41). — С. 47–54.
15. Aleksandrova N. P. Chysow V. V. The usage of integral equations hereditary theories for calculating changes measures in the theory of damage when exposed to repeated loads //// Magazine of Civil Engineering, 2016, No.2. Article in Press.
16. Чусов В. В. Модифицированные критерии Писаренко-Лебедева и Кулона-Мора, учитывающие меры теории накапливания повреждений // Молодой ученый. — 2016. — № 9 (113). — С. 338–341.
17. Чусов В. В. Применение теории накапливания повреждений в условиях пластичности асфальтобетона для расчета дорожных покрытий по сопротивлению сдвигу // Молодой ученый. — 2016. — № 6 (110). — С. 221–227.
18. Новиков А. Ю. Учет поврежденности монолитных и дискретных материалов при проектировании дорожных конструкций // Молодой ученый. — 2016. — № 8 (112). — С. 265–270.
19. Чусов В. В., Александрова Н. П. Два способа расчета мер теории накапливания // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016 — С. 271–275.
20. Кузин Н. В. Расчет пластических смещений асфальтобетонных порожных покрытий // Молодой ученый. — 2016. — № 10 (114). — С. 253–255.
21. Кузин Н. В. Исследование пластичности дорожных асфальтобетонов // Молодой ученый. — 2016. — № 10 (114). — С. 255–257.
22. Кузин В. Н., Александров А. С. Об изменении напряжения вертикального сжатия в дорожных конструкциях // Известия Орловского государственного технического университета. Серия: Строительство и транспорт. — 2007. № 4–16. — С. 221–225.
23. Foster С. R., Ahlvin R. G. Stresses and deflections induced by a uniform circular load. // Proc. Highway Research Board. — 1954. — Vol. 33. — P. 236–246.
24. Craig R. F. Soil Mechanics. — Seventh edition. Department of Civil Engineering, University of Dundee, UK. — Published by Taylor & Francis e-Library, London and New York, 2004. — 447 p.
25. Александрова Н. П. Модифицированные модели для расчета главных напряжений в грунте земляного полотна // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». Омск, 2013. — С. 236–246.
26. Александрова Н. П., Семенова Т. В., Долгих Г. В. Совершенствование моделей расчета главных напряжений и девиатора в грунте земляного полотна // Вестник СИБАДИ. — 2014. — № 2 (36). С. 49–54.
27. Александров А. С. Один из путей расчета минимальных главных напряжений в грунтах земляного полотна / А. С. Александров // В сборнике: Архитектура. Строительство. Транспорт. Технологии. Инновации Материалы Международного конгресса ФГБОУ ВПО «СибАДИ». — Омск, СибАДИ, 2013. — С. 217–228.
28. Александров А. С., Александрова Н. П., Долгих Г. В. Модифицированные модели для расчета главных напряжений в дорожных конструкциях из дискретных материалов // Строительные материалы. — 2012. — № 10. — С. 14–17.
29. Александров А. С., Долгих Г. В. Способ определения минимального главного напряжения. Часть 1. В грунтах земляного полотна. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016 — С. 64–68.
30. Александров А. С., Долгих Г. В. Способ определения минимального главного напряжения. Часть 2. В слоях дорожной одежды из дискретных материалов // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 69–73.
31. Долгих Г. В. Расчет грунтов земляного полотна по критерию безопасных давлений // Вестник Сибирской государственной автомобильно-дорожной академии. — 2013. — № 6 (34). — С. 43–49.
32. Долгих Г. В. Применение критерия безопасных давлений для расчета дорожных конструкций по сопротивлению сдвигу в грунте земляного полотна // // В сборнике: Политранспортные системы материалы VIII Международной научно-технической конференции в рамках года науки Россия — ЕС. Новосибирск: СГУПС, 2015. — С. 176–182.
33. Александров А. С., Долгих Г. В., Калинин А. Л. О допускаемых давлениях на грунты земляного полотна и слои дорожной одежды // Наука и техника в дорожной отрасли. — 2012. № 2. — С. 10–13.
34. Долгих Г. В. Расчет нежестких дорожных одежд по критерию безопасных давлений на глинистые грунты земляного полотна // Автореф. Дис. канд. техн. наук. — Омск: СибАДИ. — 2014. — 20 с.
35. Долгих Г. В. Применение безопасного давления в качестве критерия расчета земляного полотна по сдвигу в грунте // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 113–117.
36. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 1. Вывод критерия. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 50–54.
37. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 2. Круги предельных напряжений. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 54–59.
38. Александров А. С. Трехпараметрическое условие пластичности Кулона–Мора. Часть 3. Определение параметров материала. // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 59–64.
39. Калинин А. Л. Способ модификации условий пластичности // В сборнике: Наука XXI века: опыт прошлого — взгляд в будущее: материала II международной научно-практической конференции — Омск, СибАДИ, 2016. — С. 59–150.
40. Кириллов А. М., Завьялов М. А. Моделирование изменения модуля упругости асфальтобетона при нагружении // Инженерно-строительный журнал. — 2015. — № 2. — С. 70–76.
41. Александров А. С. Применение теории наследственной ползучести к расчету деформаций при воздействии повторных нагрузок: монография. — Омск: СибАДИ, 2014. — 152 с.







