Рассматривается применение модели пешеходных потоков (движения людей) SIgMA.CA для моделирования процесса выхода людей из помещений Камерного и Малого залов Красноярской филармонии. Исследуется динамика движения и время выхода. Модельное время выхода сравнивается со временем, полученным с помощью упрощенно-аналитической модели из «Методики определения расчетных величин пожарного риска в зданиях, сооружениях и строениях различных классов различной функциональной пожарной опасности».
Ключевые слова: модель пешеходных потоков, модель движения людей-пешеходов, эвакуация.
Введение
В моделях пешеходных потоков рассматривается передвижение людей из одной точки пространства в другую. Такие модели применяются для организации движения людских потоков в местах массового скопления людей (стадионы, торговые центры, вокзалы и т.д.), для анализа процесса эвакуации из зданий и сооружений (расчет времени эвакуации, выявление участков повышенной плотности и т.д.).
В настоящее время данное направление активно развивается (в основном на западе). Наибольшую популярность имеют имитационные модели, визуализирующие движение людей и позволяющие рассматривать движение каждого человека. Среди таких моделей выделяются модель социальных сил (SocialForcemodel) [1] и модели на основе клеточных автоматов. В данной работе рассматривается модель динамики пешеходов SIgMA.CA [2–3], основанная на клеточно-автоматном подходе, а именно FloorField модели [4–5].
В России для нахождения времени эвакуации из помещений и зданий применяют модели из «Методики определения расчетных величин пожарного риска в зданиях, сооружениях и строениях различных классов различной функциональной пожарной опасности» [6]: упрощенно-аналитическая модель движения людского потока, математическая модель индивидуально-поточного движения людей из здания и имитационно-стохастическая модель движения людских потоков. Выбор способа определения расчетного времени эвакуации производится с учетом специфических особенностей объемно-планировочных решений здания, а также особенностей контингента (его однородности) людей, находящихся в нем.
Упрощенно-аналитическая (УА) модель пришла в Методику из ГОСТ 12.1.004-91 «Пожарная безопасность. Общие требования», имеет ограниченный набор формул и позволяет находить время эвакуации, но непосредственно движение людей-пешеходов не моделируется. Также не учитываются переформирование потока, его растекание и разуплотнение, закономерности движения по участкам «неограниченной» и переменной ширины [7]. Но, с другой стороны, УА модель является наиболее простой, отработанной и широко применяемой для определения времени эвакуации из зданий.
Краткое описание модели пешеходных потоков SIgMA.CA
Известны геометрия рассматриваемого пространства и начальное расположение частиц (людей) в этом пространстве. Пространство представляет собой плоскость, разбитую на ячейки 40см х 40см, которые могут быть свободными, либо занятыми только одной частицей. В ячейках также могут располагаться стены и другие недвижимые препятствия.
Целью передвижения частиц является ближайший (или заданный) выход. На каждом временном шаге частица может переместиться в одну из четырех свободных соседних ячеек или остаться на месте (окрестность фон Неймана). Направление частицы предполагается случайным и определяется на основе вероятностей переходов в каждом направлении для каждой частицы в каждый дискретный шаг времени и набором правил переходов.
Полагается, что геометрия рассматриваемого пространства «известна» частицам и отражена в поле S [4], котороесовпадает с рассматриваемой областью и также разбито на ячейки. В ячейках поля хранятся кратчайшие расстояния до ближайшего выхода. Оно может быть интерпретировано, как карта местности.
Правила переходов применяются синхронно (или параллельно) и заключаются в следующем. На каждом временном шаге вычисляются переходные вероятности, и выбирается направление перемещения. Если две или более частицы претендуют на одну и ту же ячейку, тогда выбирается одна для перемещения, остальные остаются на прежних местах. Стоит отметить, что вероятность перехода в занятую ячейку в общем случае не равна нулю. Частице, выбравшей занятое направление, предоставляется возможность выбрать другое направление для перехода либо остаться на прежнем месте.
При вычислении переходных вероятностей учитывается карта местности поле S, желание частиц двигаться по направлению к выходу и держаться на некотором расстоянии от других людей и от препятствий, что регулируется параметрами модели ![]() ,
, ![]() ,
, ![]() и
и ![]() . Варьирование этими параметрами позволяет воспроизводить различные ситуации: движение в условиях плохой видимости, строго направленное движение, использование частицами кратчайшего или альтернативного пути и т.д.
. Варьирование этими параметрами позволяет воспроизводить различные ситуации: движение в условиях плохой видимости, строго направленное движение, использование частицами кратчайшего или альтернативного пути и т.д.
Несмотря на то, что направление движение частицы является случайной величиной, вероятности переходов вычисляются таким образом, чтобы придавать больший вес нужным направлениям, для реализации таких свойств движения человека, как направленность движения к цели следования, психологическое отталкивание от стен и от других участников движения, стратегии кратчайшего и быстрого пути.
Результаты исследования
На рис. 1 и рис. 2 представлены расчетные схемы эвакуации (взяты из расчетного обоснования к мероприятиям по обеспечению пожарной безопасности объекта «Реконструкция Красноярской краевой филармонии» [8] и геометрии пространств для модели с начальным расположением частиц. Серым цветом обозначены стены и ряды кресел, черным – частицы, светло-серым – выход.

Рис. 1. Геометрия Камерного зала: по расчетной схеме (слева), в модели (справа)

Рис. 2. Геометрия МКЗ: по расчетной схеме (два рисунка слева), в модели (справа)
Параметры модели ![]() ,
, ![]() . Количество частиц: для Камерного зала N=154, для Малого зала (МКЗ) N=245. Было произведено M=1000 экспериментов.
. Количество частиц: для Камерного зала N=154, для Малого зала (МКЗ) N=245. Было произведено M=1000 экспериментов.
Рассматривалось два сценария выхода частиц из области.
1. Сценарий по расчетной схеме: каждой частице назначен определенный выход согласно расчетной схеме (рис. 1 и рис. 2), где пути эвакуации обозначены стрелками.
2. Свободный сценарий: выходы изначально не назначены и выбираются в процессе эвакуации (как правило, кратчайший путь к выходу).
Динамика модели исследуется с помощью снимков движения в определенные моменты времени t и интенсивности движения частиц по ячейкам пространства. Интенсивность движения – интегральная характеристика, отражающая количество частиц прошедших через данную ячейку в течение рассматриваемого отрезка времени (в данном случае в течение всего процесса эвакуации). Чем темнее цвет, тем выше интенсивность движения по ячейкам.
Камерный зал.Рассмотрим динамику движения частиц в зависимости от сценария. Здесь по расчетной схеме частицы полностью используют проходы как центральный, так и боковые (при t=0.05 мин и t=0.3 мин, интенсивность движения) (рис. 3). Nэв– количество вышедших из области частиц на момент времени t. При свободном сценарии используется только центральный и ближайший к выходу боковой проход (при t=0.05 мин и t=0.3 мин, интенсивность движения) (рис. 4). Все частицы стремятся идти по кратчайшему пути, поэтому дальний от выхода боковой проход не используется. В итоге происходит задержка движения в ближайшем к выходу боковом проходе и в центральном проходе (рис. 4). В сценарии по расчетной схеме скопление возникает только в центральном проходе из-за большого количества частиц (при t=0.8 мин) (рис. 3).
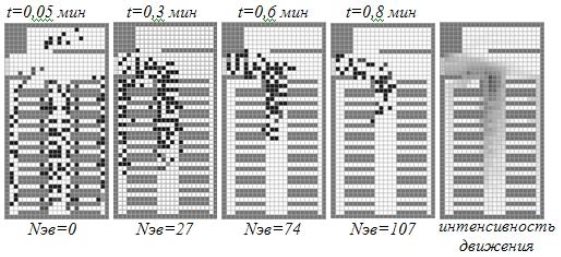
Рис. 3. Динамика движения в Камерном зале, сценарий по расчетной схеме

Рис. 4. Динамика движения в Камерном зале, свободный сценарий
На рис. 5 представлено распределение (гистограммы частот) времени выхода частиц для рассмотренных сценариев по M=1000 экспериментов. Для сценария по расчетной схеме математическое ожидание времени выхода составляет ![]() =1.3584 мин, дисперсия времени D=0.08
=1.3584 мин, дисперсия времени D=0.08 ![]() . Для свободного сценария:
. Для свободного сценария: ![]() =1.3579 мин, D=0.06
=1.3579 мин, D=0.06 ![]() .
.
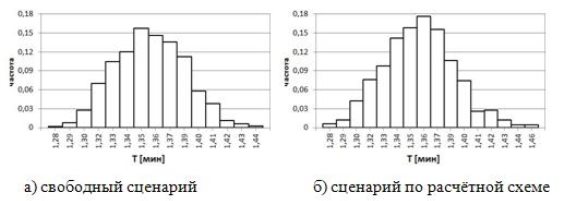
Рис. 5. Распределение времени эвакуации для Камерного зала
В модели время t [шаг] дискретно и ![]() ,
, ![]() . Пусть T – время выхода частиц из области, измеренное в дискретных шагах. Переход частицы в соседнюю ячейку отождествляется с осуществлением человеком одного шага в реальности. Обозначим за
. Пусть T – время выхода частиц из области, измеренное в дискретных шагах. Переход частицы в соседнюю ячейку отождествляется с осуществлением человеком одного шага в реальности. Обозначим за ![]() [мин] – время для осуществления человеком одного шага,
[мин] – время для осуществления человеком одного шага, ![]() =путь/скорость. «Путь» равен 0,4 м (принятый в модели размер ячейки). Для определения скорости используется аналитическая зависимость скорости от плотности потока из [6]. Здесь
=путь/скорость. «Путь» равен 0,4 м (принятый в модели размер ячейки). Для определения скорости используется аналитическая зависимость скорости от плотности потока из [6]. Здесь ![]() выбрано из предположения, что в среднем частицы двигаются с плотностью 0.4 [
выбрано из предположения, что в среднем частицы двигаются с плотностью 0.4 [![]() /
/![]() ], а скорость берется при активном движении, так как предполагается, что эвакуация происходит во время ЧС. Из этого следует, что
], а скорость берется при активном движении, так как предполагается, что эвакуация происходит во время ЧС. Из этого следует, что ![]() =0.4м / 0.572м
=0.4м / 0.572м ![]() =0.0116 мин. Таким образом, можно получить время эвакуации в естественных единицах измерения (в минутах или секундах) T[мин]=T[шаг]*
=0.0116 мин. Таким образом, можно получить время эвакуации в естественных единицах измерения (в минутах или секундах) T[мин]=T[шаг]*![]() [мин].
[мин].
В [8] получено время эвакуации (расчетное) из Камерного зала, согласно УА модели из методики [6]. Расчетное время эвакуации составляет 1.39 мин. Там же указано и необходимое время эвакуации, равное 2 мин (это время, за которое один из опасных факторов пожара (повышенная температура среды; дым, приводящий к потере видимости; токсичные газы; пониженная концентрация кислорода) достигнет предельно допустимого для человека значения). Модельное время эвакуации близко к расчетному (меньше примерно на 1.8 секунд) и не превышает необходимого. В данном случае даже максимальные времена эвакуации, полученные моделью (рис. 5), не превышают необходимого.
Малый концертный зал.Динамика в МКЗ следующая. В сценарии по расчетной схеме частицы с верхних рядов выходят быстрее, чем с нижних (рис. 6при t=1.05 мин). Но с другой стороны перед нижним выходом возникает скопление. При свободном сценарии один ряд частиц, который при сценарии по расчетной схеме двигался к нижнему выходу, двигается к верхнему (рис. 7). Это приводит к тому, что в момент времени t=1.4 мин в области меньше частиц, чем в тот же момент при сценарии по расчетной схеме. При свободном сценарии интенсивность движения более равномерно распределена между двумя выходами (рис. 6 и рис. 7). Поэтому можно сказать, что нижний выход в сценарии по расчетной схеме больше загружен.

Рис. 6. Динамика движения в МКЗ, сценарий по расчетной схеме

Рис. 7. Динамика движения в МКЗ, свободный сценарий
На рис. 8 представлено распределение времени выхода для рассмотренных сценариев выхода из МКЗ по M=1000 экспериментам. Для сценария по расчетной схеме математическое ожидание времени выхода составляет ![]() =1.83 мин, дисперсия времени D=0.04
=1.83 мин, дисперсия времени D=0.04 ![]() . Для свободного сценария:
. Для свободного сценария: ![]() =1.64 мин, D=0.,04
=1.64 мин, D=0.,04 ![]() . Здесь, в отличие от примера для Камерного зала, время эвакуации для свободного сценария меньше, чем для сценария по расчетной схеме.
. Здесь, в отличие от примера для Камерного зала, время эвакуации для свободного сценария меньше, чем для сценария по расчетной схеме.
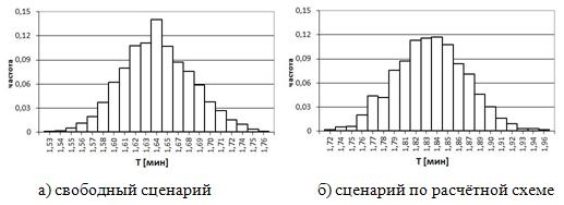
Рис. 8. Распределение времени эвакуации для МКЗ
Расчетное время эвакуации, вычисленное по УА модели, составляет 1.53 мин [8]. Необходимое время эвакуации 2 мин. Модельное время эвакуации превышает расчетное. Разница составляет 18 сек для сценария по расчетной схеме и 6.6 сек для свободного. Тем не менее модельные времена не превышают необходимого.
Заключение
Таким образом показано, что с помощью модели SIgMA.CA можно рассматривать различные сценарии эвакуации (в плане назначения частицам определенного выхода) с целью выбора наиболее подходящего, при котором минимизируется время эвакуации. Время эвакуации, полученное с помощью модели SIgMA.CA, не всегда близко к расчетному (по УА модели из Методики [6]) и может превышать его, то есть время оценивается с запасом. Но с другой стороны, модельные времена эвакуации не превышают необходимого времени. Можно сказать, что еще раз подтверждается выполнение условия своевременности эвакуации из данных помещений. К плюсам модели относится то, что она позволяет находить не одно значение времени эвакуации, а его распределение.
Литература:
- Helbing D., Molnar P. Social force model for pedestrian dynamics // Physical Review E. − 1995. − Vol. 51. − P. 4282–4286.
- Kirik E., Yurgel’yan T., Krouglov D. On realizing the shortest time strategy in a CA FF pedestrian dynamics model// Cybernetics and Systems. − 2011. − Vol. 42(1). − P. 1–15.
- Kirik E., Vitova T. Cellular Automata Pedestrian Movement Model SIgMA.CA: Model Parameters as an Instrument to Regulate Movement Regimes // Cellular Automata. Lecture Notes in Computer Science. − 2014. − Vol. 8751. − P. 501–507.
- Kirchner A., Schadschneider A. Simulation of evacuation processes using a bionics-inspried cellular automaton model for pedestrian dynamics // Physica A. − 2002. − Vol. 312. − P. 260–276.
- Nishinari K., Kirchner A., Namazi A., Schadschneider A. Extended floor field CA model for evacuation dynamics // IEICE Transactions on Information and Systems. – 2004. – Vol. E87-D, No. 3. – P. 726–732.
- Методика определения расчетных величин пожарного риска в зданиях, сооружениях и строениях различных классов функциональной пожарной опасности: приложение к Приказу МЧС России от 30 июня 2009 г. № 382: зарегистр. в Минюсте РФ 6 августа 2009 г., рег. № 14486 // МЧС России. URL: http://www.mchs.gov.ru/law/Normativno_pravovie_akti_Ministerstva/item/5380580 (дата обращения: 04.03.2016).
- Самошин Д.А. Расчет времени эвакуации людей. Проблемы и перспективы // Пожаровзврывобезопасность. – 2004. – № 1. – C. 33–46.
- Расчетное обоснование к мероприятиям по обеспечению пожарной безопасности для объекта «Реконструкция Красноярской краевой филармонии», ООО «ПроектСтройСервис», шифр-265-07-ПБ.РО.







