Представлена реализация метода генерации расчетных акселерограмм, рекомендуемая Приложением 3 РБ-06-98 [1]. На основе данного метода и исследований Ф.Ф. Аптикаева [2] разработан алгоритм генерирования сейсмических воздействий на основе заданных спектров реакций. Создано программное обеспечение (GOSS), реализующее данный алгоритм.
Введение
Спектры реакций (ответов) одна из наиболее важных, полезных и широко используемых концепций в теории и практике расчетов сооружений на сейсмостойкость. Предложенная более 80 лет назад, в настоящее время эта концепция используется практически во всех зарубежных нормативных документах и руководствах по расчету сооружений на сейсмостойкость.
В Российских нормах для оценки сейсмических воздействий используется понятие «спектральный коэффициент динамичности»-
, кривые которого строятся как функции периода свободных колебаний осциллятора. Это практически та же концепция, названная по-другому[3].
Задача расчета спектров реакций детально изучена, а также существуют эффективные алгоритмы расчета (см. [4]). В свою очередь обратная задача – синтезирование расчетных акселерограмм из заданных спектров реакций для проектирования зданий и сооружений, в частности, особо ответственных объектов, стоит уже давно. К сожалению, на данный момент есть лишь общие рекомендации касательно генерации сейсмических воздействий из спектров реакций [2]. С другой стороны, в работах Ф.Ф. Аптикаева [2] достаточно эмпирических формул, позволяющих параметризировать форму спектра реакций, а также форму огибающей сейсмического события.
Таким образом, объединив результаты Ф.Ф. Аптикаева, рекомендации, данные в [2], и алгоритмы численного расчета спектров реакций, была создана программа, позволяющая синтезировать расчетные сейсмические воздействия на основе заданных спектров реакций.
Форма спектра реакции
Общепринятая форма спектра реакций получается путем осреднения спектральных уровней на каждой частоте. Однако, согласно правилам параметризации, использовать размерную величину (частоту) для построения безразмерного параметра (форма по определению величина безразмерная) не совсем корректно. Такой способ ведет к снижению уровня «среднего» спектра и расширению полосы частот.
Методика оценки формы спектра реакции и внутренние взаимозависимости между параметрами спектров рассмотрены в работе [2]. Рекомендуется использовать следующую систему параметризации – спектры нормированы как по спектральному уровню SA, так и по преобладающей частоте f0(рис. 1).
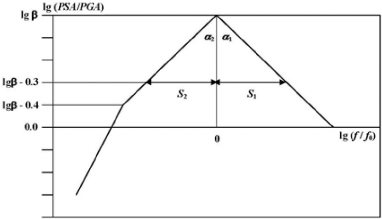
Рис. 1. Схема параметризации спектра реакции (Ф.Ф. Аптикаев, 2012 г.)
S – логарифмическая ширина спектра реакции S2+S1; измеряемая между частотами, на которых в первый и последний раз уровень спектра достиг половины его максимального значения.
β – максимальное значение коэффициента динамического усиления (величина безразмерная);
f0 – преобладающая колебаний.
Среднее значение β на более интенсивной горизонтальной компоненте принимается 3.2. Для перехода от средней формы спектра к реальному спектру надо оценить ширину, ожидаемый преобладающий период и уровень спектра.
В среднем ширина спектра S равна двум октавам со стандартным отклонением 0.20 ед. дес. лог.:
S = 0.6 + С1 + С2 ± 0.20,(1)
где С1 = –0.05 для взбросов, 0.0 для сдвигов и 0.05 для сбросов; С2 = –0.1 для грунтов первой категории, 0.0 для грунтов второй категории и 0.1 для грунтов третьей категории [2].
Алгоритм синтезирования расчетных сейсмических воздействий
В данной работе использован метод генерации расчетной акселерограммы, рекомендуемый Приложением 3 РБ-06-98. Акселерограмма, соответствующая спектру динамического усиления, может быть записана
,(2)
где
– огибающая сигнала; фазовые углы 
представляют собой равномерно распределенные в интервале от 0 до 2π случайные величины; n – количество частот; ω – частоты.
В качестве первого приближения для 
используются значения, непосредственно взятые с заданной кривой 
для соответствующих значений частот 
.
Следующее приближение
,(3)
где 
– в нашем случае обобщенный спектр динамического усиления, а 
– кривая, полученная при первом шаге итерации.
Нужная точность совпадения расчетного спектра реакций с заданным получается после ряда итераций (по умолчанию 30). Если после указанного количества итераций величина разброса расчетного спектра реакций больше, чем заданная величина допустимого разброса, – заново генерируется набор фазовых углов 
и расчет проводится сначала.
Для перехода от базовой акселерограммы к расчетной значения первой следует умножить на PGA.
Для построения огибающей использована эмпирическая формула [2]:
,(4)
где t – время, τ – длительность основной фазы колебаний по Ф.Ф. Аптикаеву определяется как интервал времени, в течение которого амплитуда огибающей колебаний превышает 1/2 максимального уровня. Для определения этой величины воспользуемся формулой [2]:
,
где коэффициент
равен 0.25 для сбросов, 0.00 для сдвигов и –0.25 для взбросов;
равняется –0.15 для грунтов 1-й категории, 0.00 для грунтов 2-й категории и 0.4 для грунтов 3-й категории. В очаговой и ближней зонах значение ширины импульса с расстоянием не изменяется
В соответствии с п. 5.3.4 РБ 06-98, при синтезировании трехкомпонентных акселерограмм необходимо обеспечивать их статистическую независимость. Две акселерограммы считаются статистически независимыми, если абсолютное значение коэффициента корреляции не превышает 0.3.
Для максимальной горизонтальной компоненты принято максимальное динамическое усиление max βX(Т) = 3.2 [1]. Для второй горизонтальной и вертикальной компонент приняты значения max βY(Т) = 3.0, max βZ(Т) = 3.0. Допускается отклонение от целевого спектра 10 %.
Значения PGA приняты для горизонтальных компонент одинаковыми, а для вертикальной компоненты 0.7 от горизонтальной.
Блок схема алгоритма расчета представлена на рис. 2.
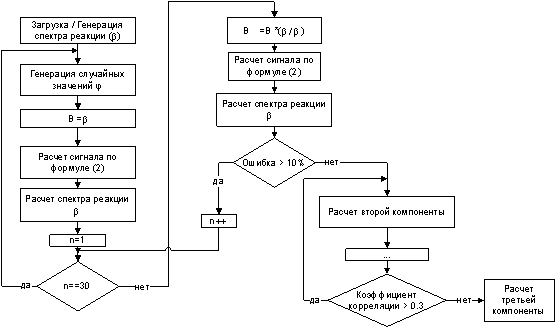
Рис. 2. Блок схема алгоритма расчета
Программа синтезирования расчетных сейсмических воздействий GOSS
На основании вышеизложенного алгоритма создана программа GOSS (рис. 3). Данная программа была написана на языке C#. В форме главного окна осуществляется задание следующих параметров:
– характеристики очага (магнитуда (Ms), расстояние (км), длительность колебаний (с), а также фокальный механизм очага (взброс, сдвиг, сброс, взбросо-сдвиг, сбросо-сдвиг));
– характеристики площадки (категория грунтов по сейсмическим свойствам, PGA выходной акселерограммы, частота дискретизации выходного сигнала);
– форма спектра реакций (существует возможность загрузки готового спектра реакций из файла либо задания формы спектра реакций на основании параметров).
На каждой итерации происходит визуализация сгенерированного сигнала, спектра Фурье и текущего спектра реакций. Все вычисления проходят в фоновом потоке. По окончанию расчетов есть возможность сохранить синтезированные акселерограммы, а также их спектры реакций, рассчитанные с различными коэффициентами затухания (20 %, 10 %, 7 %, 5 %, 4 %, 2 %, 0.5 %). На рис. 4 показаны результаты синтезирования акселерограмм для здания уровней МРЗ для 50% обеспеченности.
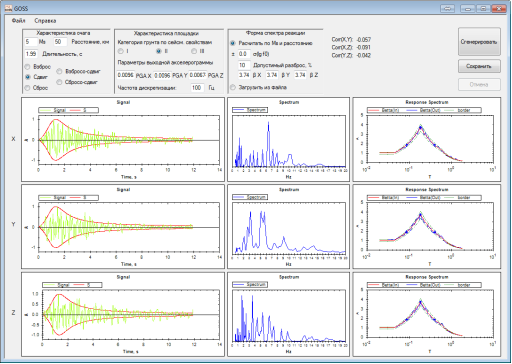
Рис. 3. Главное окно программы GOSS
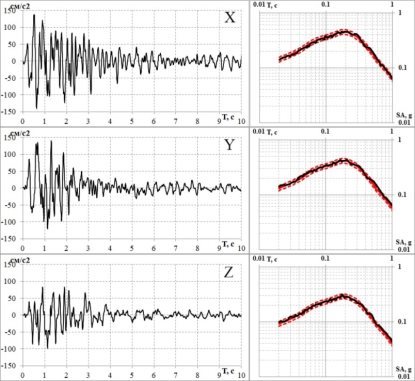
Рис. 4. Синтезированная трехкомпонентная акселерограмма 50 % обеспеченности уровня
воздействия ПЗ и соответствующие ей спектры реакции для здания
Заключение
Разработаны методические и алгоритмические основы расчета генерации сейсмических воздействий по заданным спектрам реакций. Разработано программное обеспечение (GOSS), реализующее указанные алгоритмы. Исследованы формы спектров реакций, заданные параметрически.
Литература:
- РБ-06-98 «Определение исходных сейсмических колебаний грунта для проектных основ».
- Аптикаев Ф.Ф. Инструментальная шкала сейсмической интенсивности. – М.: Наука и образование, 2012. – 176 с.
- Курбацкий Е.Н., Баев Л.В. Спектры максимальных реакций (откликов) конструкций на сейсмические и техногенные динамические воздействия.
- NewmarkN.M. A method of computation for structural dynamics // Journal of Engineering Mechanics, ASCE, 1959. – Vol. 85, (EM3). – P. 67–94.
