Из-за различий в характеристиках детекторных элементов и других факторов, связанных с электроникой в снимках полученных дистанционным зондированием часто присутствует полосовой шум и пропущенные пиксели. Чтобы ограничить пространство решений в соответствии с априорными знаниями в данной статье мы описываем метод максимума апостериорной вероятности (MAP) для обеих проблем, и для полосовых шумов, и для пропущенных пикселей. В методе MAP функция плотности вероятности (PDF) основывается на линейной модели наблюдения и на модели Хубера-Маркова. Метод оптимизации градиентного спуска используется для получения необходимого изображения. Предложенный алгоритм был протестирован на изображениях различных датчиков. Экспериментальные результаты показывают, что он имеет высокую производительность с точки зрения, как количественных измерений, так и с визуальной оценки.
Ключевые слова: полосовой шум, дистанционное зондирование, пиксели, апостериорная вероятность, модель Хубера-Маркова, зарисовывание изображения.
Качество изображений, полученных дистанционным зондированием, часто ухудшается из-за полосовых шумов и линейных или случайных «плохих» пикселей. Восстановление пропущенных пикселей иногда носит название замена «плохих» пикселей. В данной работе мы используем другой термин — зарисовывание изображения, широко известный в области обработки цифровых изображений [1].
Методы устранения шума можно разделить на алгоритмы частотной области и алгоритмы пространственной области. Наипростейший алгоритм частотной области обработка изображения с фильтром нижних частот с использованием дискретного преобразования Фурье. Этот метод имеет преимущество в том, что его можно использовать для «гео-выпрямления» изображения. Но он часто не удаляет лишние полосы и приводит к значительному размыванию в пределах изображения [2]. Был предложен метод, с этапами распознавания индуцировано-частотных компонентов с использованием спектра мощности, затем удаления полосового шума с помощью мощности конечно-импульсного фильтра. Некоторые исследователи предлагают устранять полосовой шум с помощью вейвлет-анализа, который использует преимущества масштабирования и свойств по обнаружению и устранению шума [2].
По проблеме зарисовывания изображения обычно используются методы ближайших соседей, среднее близлежащих точек или медиана близлежащих точек [3]. Основной недостаток этих методов состоит в том, что они могут применяться только тогда, когда площадь пропущенных пикселей очень мала (один или два пикселя).
- Предложенный алгоритм
1.1 Математическая модель наблюдения
Пусть ![]() и
и ![]() обозначают входную измеряемую яркость и выходные координаты соответственно. Отношения между
обозначают входную измеряемую яркость и выходные координаты соответственно. Отношения между ![]() и
и ![]() могут быть связаны линейной или нелинейной функцией. В данной работе мы предполагаем, что процесс деградации может определяться линейно, как в работе [4], но мы допускаем существование ошибки линейного предположения, как
могут быть связаны линейной или нелинейной функцией. В данной работе мы предполагаем, что процесс деградации может определяться линейно, как в работе [4], но мы допускаем существование ошибки линейного предположения, как
![]() (1.1)
(1.1)
где,
![]() (1.2)
(1.2)
В модели ![]() является лексикографически упорядоченным вектором наблюдаемого изображения,
является лексикографически упорядоченным вектором наблюдаемого изображения, ![]() представляет собой необходимое изображение;
представляет собой необходимое изображение; ![]() — диагональная матрица, диагональными элементами которой являются коэффициенты усиления всех пикселей;
— диагональная матрица, диагональными элементами которой являются коэффициенты усиления всех пикселей; ![]() — вектор смещения,
— вектор смещения, ![]() — вектор шума.
— вектор шума.
1.2 Модель восстановления MAP
В последние годы метод максимума апостериорной вероятности (MAP) используется как базовый метод во многих сферах в решениях некорректных обратных задач [5] такие как зашумление изображения, размытие изображения [6], восстановление сверхвысокого разрешения [2] и другие. Наша цель реализовать метод максимума апостериорной вероятности в устранении шума на изображении и в зарисовывании пропущенных пикселей. Это может быть вычислено следующим образом
![]() (1.3)
(1.3)
Применяя правило Байеса, уравнение (1.3) примет вид
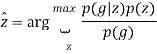 (1.4)
(1.4)
Так как ![]() не зависит от параметра
не зависит от параметра ![]() ,
, ![]() можно считать константой и, следовательно, уравнение (1.4) можно переписать в виде
можно считать константой и, следовательно, уравнение (1.4) можно переписать в виде
![]() (1.5)
(1.5)
Первая функция плотности вероятности в уравнении (1.5) является функцией плотности правдоподобия. Она определяется плотностью вероятности вектора шума в уравнении (1.2), т. е. ![]() . Поскольку различные пиксели могут разлагаться в разной степени, мы предполагаем, что шум не одинаковый, но по-прежнему независимый. В этих предположениях плотность вероятности задается
. Поскольку различные пиксели могут разлагаться в разной степени, мы предполагаем, что шум не одинаковый, но по-прежнему независимый. В этих предположениях плотность вероятности задается
где, ![]() — постоянная величина,
— постоянная величина, ![]() — ковариационная матрица, которая описывает уровень шума. Так как предполагается что шум независимая величина,
— ковариационная матрица, которая описывает уровень шума. Так как предполагается что шум независимая величина, ![]() является диагональной матрицей, содержащей дисперсии шума. Таким образом, уравнение (1.6) можно переписать в следующем виде
является диагональной матрицей, содержащей дисперсии шума. Таким образом, уравнение (1.6) можно переписать в следующем виде
![]() (1.7)
(1.7)
где ![]() также диагональная матрица. Вторая функция плотности в уравнении (1.5) является предшествующим изображением, который накладывает пространственные ограничения целостности на изображение. Эти ограничения включают в себя положительность, гладкость и т. д. Здесь мы используем ограничения модели Хубера-Маркова. Эта модель может правильно соблюдать ограничения и сохранять подробную информацию в изображении. Это обозначается следующим образом
также диагональная матрица. Вторая функция плотности в уравнении (1.5) является предшествующим изображением, который накладывает пространственные ограничения целостности на изображение. Эти ограничения включают в себя положительность, гладкость и т. д. Здесь мы используем ограничения модели Хубера-Маркова. Эта модель может правильно соблюдать ограничения и сохранять подробную информацию в изображении. Это обозначается следующим образом
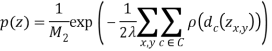 (1.8)
(1.8)
В этом выражении ![]() константа, с является кликой во множестве кликов всех изображении C, величина
константа, с является кликой во множестве кликов всех изображении C, величина ![]() измерения пространственной активности пикселя
измерения пространственной активности пикселя ![]() , которая часто формируется разностью первого или второго порядка, а ρ (⋅) функция Хубера, определяющаяся следующим образом
, которая часто формируется разностью первого или второго порядка, а ρ (⋅) функция Хубера, определяющаяся следующим образом
![]() (1.9)
(1.9)
где, ![]() является пороговым значением разделения квадратичного и линейного участка. Для
является пороговым значением разделения квадратичного и линейного участка. Для ![]() мы вычисляем конечные разности второго порядка в четырех соседних кликах для каждого положения на изображении (x,y)
мы вычисляем конечные разности второго порядка в четырех соседних кликах для каждого положения на изображении (x,y)
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
Подставляя значения (1.7) и (1.8) в уравнение (1.5), используя логарифмическую функцию и выполнив некоторые операции, значения ![]() и
и ![]() могут быть опущены. Максимизация этого распределения вероятностей эквивалентна следующей регуляризованной задаче мининума:
могут быть опущены. Максимизация этого распределения вероятностей эквивалентна следующей регуляризованной задаче мининума:
![]() (1.14)
(1.14)
где, ![]() называется параметром регуляризации.
называется параметром регуляризации.
1.3 Решение
Метод оптимизации градиентного спуска используется для задачи минимума в уравнении (1.14). Дифференцируя функцию затрат по ![]() мы имеем
мы имеем
![]() (1.15)
(1.15)
где, ![]() производная от параметра регуляризации. Затем необходимое изображение получаем, используя последовательные приблизительные значения итерации
производная от параметра регуляризации. Затем необходимое изображение получаем, используя последовательные приблизительные значения итерации
![]() (1.16)
(1.16)
где ![]() — число итерации,
— число итерации, ![]() размер шага.
размер шага.
1.4 Определение параметров
Для того чтобы использовать модель наблюдения, параметры
Матрица ![]() является диагональной и ее элементы представляют собой обратную величину шума стандартного отклонения в разных позициях пикселя. Для удобства мы нормализуем значения элементов в диапазоне 0
является диагональной и ее элементы представляют собой обратную величину шума стандартного отклонения в разных позициях пикселя. Для удобства мы нормализуем значения элементов в диапазоне 0![]() . Разница вызванная масштабированием может быть уравновешена параметром
. Разница вызванная масштабированием может быть уравновешена параметром ![]() (определяется эвристически). Для всех «хороших» пикселей максимальное значение соответствующих элементов устанавливается как 1. Для пропущенных пикселей наоборот, значения должны быть 0. Значения элементов других «плохих» пикселей определяются между 0 и 1, и они соотносятся с локальным уровнем активности, действительностью согласования моментов и т. д. Как правило, мы можем выбрать малые значения элементов для восстановления информации из соседей, используя предварительное ограничение. С другой стороны крупные значения должны быть выбраны для острых (резких) областей для сохранения высокочастотной информации. Мы используем стандартное отклонение как измерение активности и простую линейную функцию для определения значения элементов.
(определяется эвристически). Для всех «хороших» пикселей максимальное значение соответствующих элементов устанавливается как 1. Для пропущенных пикселей наоборот, значения должны быть 0. Значения элементов других «плохих» пикселей определяются между 0 и 1, и они соотносятся с локальным уровнем активности, действительностью согласования моментов и т. д. Как правило, мы можем выбрать малые значения элементов для восстановления информации из соседей, используя предварительное ограничение. С другой стороны крупные значения должны быть выбраны для острых (резких) областей для сохранения высокочастотной информации. Мы используем стандартное отклонение как измерение активности и простую линейную функцию для определения значения элементов.
- Экспериментальные результаты
2.1 Эксперименты по устранению полосового шума
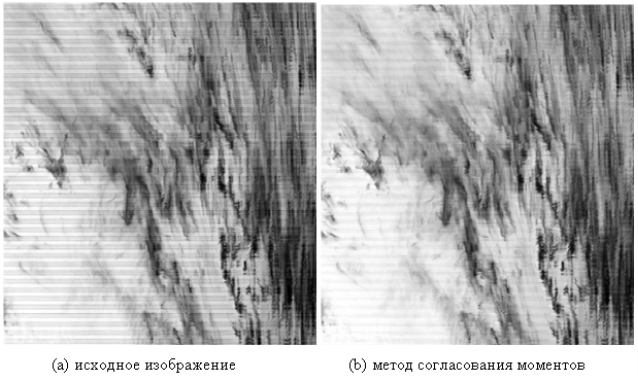
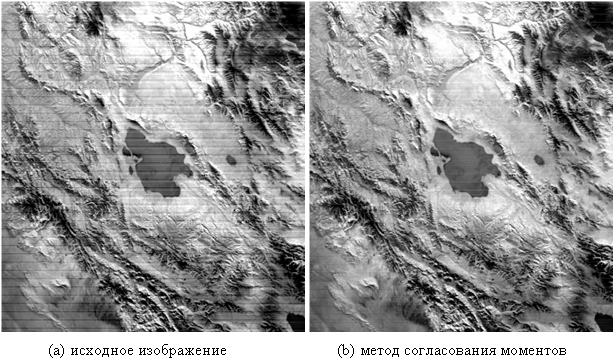
Предложенный алгоритм был протестирован на снимках MODIS (ModerateResolutionImagingSpectrometer) на борту платформы Terra и Aqua. Отрезок размером 400![]() 400 был извлечен из исходных изображений в качестве экспериментальных данных. Для удобства расчета и отображения исходные данные закодированы по 8-битной шкале. Исходные и обработанные изображения на платформах Terra и Aqua показаны на рисунках 1 и 2 соответственно. Можно заметить, что метод согласования моментов может значительно улучшить качество изображения, но все еще существуют значительные флуктуации яркости в пределах полученного изображения. Предложенный алгоритм, тем не менее, обеспечивает гораздо более надежное устранение полосового шума с визуальной точки зрения. На рисунке 3 приведены графики по средним цифровым значениям перпендикуляров к сейсмическому профилю с использованием предложенного алгоритма. Можно заметить, что крутые колебания исходных данных сильно уменьшается на изображении без полосового шума. Средние значения спектров мощности исходных и обработанных изображении приведены на рисунке 4. Для лучшей визуализации снижения уровня шума, очень высокие спектральные величины не были нанесены. Можно легко увидеть, что значение спектра мощности частотных составляющих, где есть импульс, существенно было уменьшено в изображении без полосового шума.
400 был извлечен из исходных изображений в качестве экспериментальных данных. Для удобства расчета и отображения исходные данные закодированы по 8-битной шкале. Исходные и обработанные изображения на платформах Terra и Aqua показаны на рисунках 1 и 2 соответственно. Можно заметить, что метод согласования моментов может значительно улучшить качество изображения, но все еще существуют значительные флуктуации яркости в пределах полученного изображения. Предложенный алгоритм, тем не менее, обеспечивает гораздо более надежное устранение полосового шума с визуальной точки зрения. На рисунке 3 приведены графики по средним цифровым значениям перпендикуляров к сейсмическому профилю с использованием предложенного алгоритма. Можно заметить, что крутые колебания исходных данных сильно уменьшается на изображении без полосового шума. Средние значения спектров мощности исходных и обработанных изображении приведены на рисунке 4. Для лучшей визуализации снижения уровня шума, очень высокие спектральные величины не были нанесены. Можно легко увидеть, что значение спектра мощности частотных составляющих, где есть импульс, существенно было уменьшено в изображении без полосового шума.
Обратный коэффициент вариации(ICV) и индекс снижения уровня шума (NR) используется, чтоб получить количественный анализ. Индекс ICV [7] определяется как
![]() (2.1)
(2.1)
где, ![]() ответный сигнал однородной области изображения, вычисляемый усреднением пикселей в пределах окна заданного размера;
ответный сигнал однородной области изображения, вычисляемый усреднением пикселей в пределах окна заданного размера; ![]() компонент шума, вычисляемый стандартным отклонением пикселя. В наших экспериментах мы выбрали две 10 × 10 однородных областей для оценки ICV.
компонент шума, вычисляемый стандартным отклонением пикселя. В наших экспериментах мы выбрали две 10 × 10 однородных областей для оценки ICV.

(с) MAP
Рис. 1. Результаты устранения шума на снимке Terra MODIS

(с) MAP
Рис. 2. Результаты устранения шума на снимке Aqua MODIS.
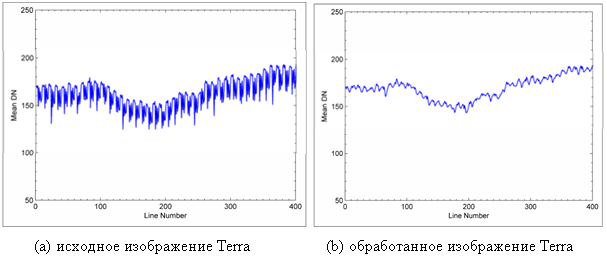
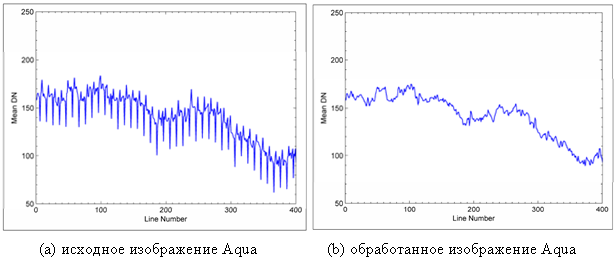
Рис. 3. Средние цифровые значения перпендикуляров к сейсмическому профилю исходных и обработанных изображении MODIS
Индекс NR [2] используется для оценки изображения в частотной области. Она определяется следующим образом
![]() (2.2)
(2.2)
где, ![]() мощность частоных составляющих, полученных полосами в исходном изображении,
мощность частоных составляющих, полученных полосами в исходном изображении, ![]() в обработаном изображении.
в обработаном изображении. ![]() и
и ![]() вычисляется по формуле
вычисляется по формуле
![]() (2.3)
(2.3)
где,
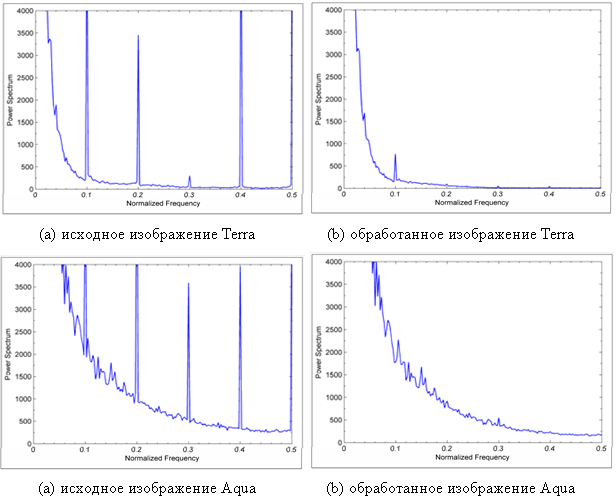
Рис. 4. Средние значения спектров мощности исходных и обработанных изображении MODIS
Таблица 1
Результаты ICV исходных иобработанных данных MODIS
|
|
Исходное |
Баттерворт |
Моменты |
Гистограмма |
Предложенное |
|
|
TerraBand28 |
Sample1 |
24.08 |
27.26 |
39.32 |
43.93 |
46.79 |
|
Sample2 |
17.27 |
23.93 |
21.82 |
21.49 |
25.87 |
|
|
Aqua Band 30 |
Sample1 |
7.94 |
14.49 |
24.42 |
22.72 |
26.83 |
|
Sample2 |
9.66 |
15.74 |
21.03 |
24.86 |
30.31 |
|
Таблица 2
Результаты оценки NR исходных иобработанных данных MODIS
|
|
Исходное |
Баттерворт |
Моменты |
Гистограмма |
Предложенное |
|
Terra Band28 |
1.00 |
4.39 |
15.96 |
17.71 |
25.81 |
|
Aqua Band 30 |
1.00 |
4.26 |
4.82 |
5.05 |
7.56 |
2.2 Эксперименты по зарисовыванию пропущенных пикселей
На рисунке 5 показаны экспериментальные результаты снимков CBERS (China- Brazil Earth Resource Satellite) по восстановлению вертикальных пропущенных пикселей. Рисунки 5(а) и 5(c) загрязнены линиями шириной 5 и 8 пикселей соответственно. Известно, что обычные методы не способны устранять такие широкие полосы. На рисунках 5(b) и 5(d) приведены результаты зарисовыванию с использованием предложенного алгоритма. Несмотря на то, потерянная информация не может быть полностью восстановлена, визуальное качество приведенных изображений очень хорошая. Рисунок 6(а) представляет собой изображение, испорченное некоторыми росчерками, а 6(b) его зарисованный результат. Можно заметить, что большая часть потерянной информации была восстановлена. Рисунок 6(с) это изображение, загрязненное «плохими» пикселями распределенных случайным образом, процентное соотношение которых составляет 60 %. Его зарисованное изображение показано на рисунке 6(d). Этот эксперимент подтверждает высокую эффективность и производительность предложенного алгоритма. Хотя такое случайное распределение «плохих» пикселей не очень хорошо знакомо многим пользователям дистанционного зондирования, это часто встречается в предварительной обработке перед распределением данных.


Рис. 5. Результаты зарисовывания снимков CBERS

Рис. 6. Результаты зарисовывания снимков IKONOS
Заключение
В этой статье мы используем метод максимума апостериорной вероятности (MAP) для двух проблем: по устранению полосового шума и зарисовывания пропущенных пикселей. Основное преимущество данного алгоритма является то, что он может ограничить пространство решений в соответствии с априорным ограничением. В экспериментах по устранению полосового шума мы тестировали данный алгоритм на изображениях MODIS платформ Terra и Aqua. Количественный анализ показал, что предложенный алгоритм обеспечивает более высокие результаты, чем обычные методы снижения шума. В экспериментах зарисовывания изображении были восстановлены снимки с вертикальными пропущенными пикселями, поцарапанные и заполненные «плохими» пикселями. Экспериментальные результаты подтвердили, что зашумленные и загрязненные изображения могут быть восстановлены с использованием метода максимума апостериорной вероятности (MAP).
Литература:
- Bertalmio, M., Sapiro, G., Caselles, V. and Ballester, C., 2000. Image inpainting, the ACM SIGGRAPH Conference on Computer Graphics, New Orleans, LA, pp. 417–424.
- Chen, J.S., Lin, H., Shao, Y. and Yang, L.M., 2006. Oblique striping removal in remote sensing imagery based on wavelet transform. International Journal of Remote Sensing, 27(8):1717–1723.
- Ratliff, B.M. et al., 2007. Dead pixel replacement in LWIR microgrid polarimeters. Optics Express, 15(12): 7596–7609.
- Gadallah, F.L., Csillag, F. and Smith, E. J. M., 2000. Destriping multisensor imagery with moment matching. International Journal of Remote Sensing, 21(12): 2505–2511.
- Borman, S. and Stevenson, R., 1998 Spatial Resolution Enhancement of Low-Resolution Image Sequences: A Comprehensive Review with Directions for Future Research. Report, Laboratory for Image and Signal Analysis (LISA), University of Notre Dame,.
- Ferrari, P.A., Frigessi, A. and de Sa, P.G., 1995. Fast Approximate Maximum a Posteriori Restoration of Multicolour Images. Journal of the Royal Statistical Society. Series B(Methodological), 57(3): 485–500.
- Nichol, J.E. and Vohora, V., 2004. Noise over water surfaces in Landsat TM images. International Journal of Remote Sensing, 25(11): 2087–2093.







