Представлены математические модели основного станочного оборудования, моделирующий алгоритм и результаты имитации работы головного станка при различных режимах обработки лесоматериалов в технологическом потоке.
Для решения поставленной в статье задачи привлечена комплекс-программа (КП) ЦЕХ, один из ранних вариантов которой опубликован в статьях [1,2]. Обоснование применения КП ЦЕХ для исследований приведено в работе [3]. В связи с разработанной методологией исследования [4] проведена проверка на адекватность математических моделей, алгоритмов и программ реальному процессу. КП ЦЕХ отвечает всем основным требованиям, предъявляемым к имитационным моделям [5,6].
Основным, значимым параметром, фигурирующим в теории производительности машин и механизмов является длительность распиловки tд сырья и полуфабрикатов на станках. Параметр tд является случайной величиной, обладающей значительной дисперсией [7].
Среди факторов, обуславливающий случайный характер tД, существуют доминирующие. Это параметры лесоматериалов и их деления. Учет их влияния на величину tД возможен различными способами. Изучение схем деления лесоматериалов показало, что основным обобщающим параметром, характеризующим деление и влияющим на величину tД, является постав или что тоже самое — число резов np, зависящее как от размерно-качественных параметров лесоматериалов, так и от размеров готовой продукции. Приняв это во внимание и на основании теории производительности машин и механизмов, величина tД для цикло-проходных станков и однопозиционных торцовочных запишется в виде tД = npt1p, а для проходных станков при продольном делении лесоматериалов tД = tM![]() + tП, где t1p — цикловое время на один рез; tM — длительность деления единицы длины лесоматериала, зависящая от постава;
+ tП, где t1p — цикловое время на один рез; tM — длительность деления единицы длины лесоматериала, зависящая от постава; ![]() — длина лесоматериала; tП — длительность циклового простоя.
— длина лесоматериала; tП — длительность циклового простоя.
Длительность цикла tД для станков группового деления круглых лесоматериалов представляют в виде двух слагаемых — длительности деления бревна tℓ и tП. Первое слагаемое определяется произведением сомножителей tМ и ![]() , а длительность циклового простоя tП, согласно теории производительности (на примере лесопильной рамы) tП = tВ — tC, где tB — время выполнения вспомогательных операций.
, а длительность циклового простоя tП, согласно теории производительности (на примере лесопильной рамы) tП = tВ — tC, где tB — время выполнения вспомогательных операций.
Длительность деления свободного конца бревна tC составляет tC = tM![]() C, где
C, где ![]() C — длина свободного конца бревна.
C — длина свободного конца бревна.
Величина tB, как известно, состоит из следующей суммы затрат на выполнение элементов цикла tB = tX + tЗ + tP + tЗЛ, где tX — время на разжим бревна и холостой ход тележки; tЗ — время загрузки тележки бревном, зажима его и ориентирования по порокам; tP — время рабочего хода; tЗЛ — время загрузки лесопильной рамы бревном и надвигания его до пил.
Длительность циклового простоя в длительности цикла можно учесть коэффициентом производительности КП tД = tℓKП. Численные значения КП зависят от средней длины распиливаемых бревен ![]() . По результатам исследования получена статистическая зависимость KП = 1,0546 е -0,2061/
. По результатам исследования получена статистическая зависимость KП = 1,0546 е -0,2061/![]() . Уравнение действительно при 1м ≤
. Уравнение действительно при 1м ≤ ![]() ≤ 6 м для одноэтажных восьмивальцовых лесопильных рам. Анализ полученного уравнения позволяет сделать вывод о минимальной длине распиливаемых бревен. При длине бревен 250 см и выше обеспечивается оптимальная производительность одноэтажных лесопильных рам.
≤ 6 м для одноэтажных восьмивальцовых лесопильных рам. Анализ полученного уравнения позволяет сделать вывод о минимальной длине распиливаемых бревен. При длине бревен 250 см и выше обеспечивается оптимальная производительность одноэтажных лесопильных рам.
Длительности деления единицы длины бревен (1м) tM для бревен по толщине из мелкой и средней групп лесоматериалов не противоречат логнормальному распределению, а из крупной — нормальному. Средние значения ![]() и СКО
и СКО ![]() для березы и осины зависят от di. Для учета поставов лесопильных рам вместо толщин бревен di введены суммарные высоты пропилов ∑h, приходящихся на одно бревно. В этой связи, среднее значение продолжительности деления бревен
для березы и осины зависят от di. Для учета поставов лесопильных рам вместо толщин бревен di введены суммарные высоты пропилов ∑h, приходящихся на одно бревно. В этой связи, среднее значение продолжительности деления бревен ![]() М толщиной di на лесопильной раме модели М с ходом пильной рамы Н, частотой вращения главного вала n принимается равным
М толщиной di на лесопильной раме модели М с ходом пильной рамы Н, частотой вращения главного вала n принимается равным ![]() = КН КО КТ КС
= КН КО КТ КС![]() , а СКО (по коэффициенту вариации случайной величины
, а СКО (по коэффициенту вариации случайной величины ![]() )
) ![]() = (
= (![]() /
/ ![]() )
)![]() , где
, где ![]() и
и ![]() — статистики случайной величины tM для коротышевой рамы РК, определяемые для березы и осины по формулам табл. 1; КН = 410/Н — коэффициент, учитывающий ход пильной рамки; КО = 215/n — коэффициент, учитывающий частоту вращения коленвала лесопильной рамы; КТ — коэффициент, учитывающий сезон работы рамы (для летних условий КТ = 1, для зимних КТ = 1,1); КС — коэффициент, учитывающий сортность бревен (для 1…2 с. КС = 0,78 … 0,85, для 3 с. — КС = 1).
— статистики случайной величины tM для коротышевой рамы РК, определяемые для березы и осины по формулам табл. 1; КН = 410/Н — коэффициент, учитывающий ход пильной рамки; КО = 215/n — коэффициент, учитывающий частоту вращения коленвала лесопильной рамы; КТ — коэффициент, учитывающий сезон работы рамы (для летних условий КТ = 1, для зимних КТ = 1,1); КС — коэффициент, учитывающий сортность бревен (для 1…2 с. КС = 0,78 … 0,85, для 3 с. — КС = 1).
Таблица 1
Регрессионные уравнения зависимостей параметров случайной величины tM от доминирующего фактора
|
Уравнения |
Коэффициенты уравнений определены при |
|
σ МБ = -0,0000007 ∑h2 + 0,0029 ∑h + 3,9890, с
σ МО = -0,0000005 ∑h2 + 0,0029 ∑h + 3,0268, с |
∑h ≥ 190 мм ∑h ≤ 1770 мм ∑h ≥ 200 мм ∑h ≤ 2130 мм |
Определение среднего значения раскроя сосновых бревен длиной 1 м![]() возможен по формуле, выведенной для дальнейшего использования:
возможен по формуле, выведенной для дальнейшего использования:
![]() =
= ![]() - [(
- [(![]() -
- ![]() )
) 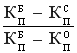 ], (1)
], (1)
где КП — коэффициент, учитывающий изменение удельного сопротивления резанию в зависимости от породы (для березы — 1,25, сосны — 1, осины — 0,85).
Вывод зависимости ![]() = ƒ(∑h) возможен при определении координат точек М (∑hmin,
= ƒ(∑h) возможен при определении координат точек М (∑hmin, ![]() ), N(∑hmax,
), N(∑hmax, ![]() ), составлении и решении двух линейных уравнений с двумя неизвестными
), составлении и решении двух линейных уравнений с двумя неизвестными
![]() = 0,0150 ∑h + 14,9079, с. (2)
= 0,0150 ∑h + 14,9079, с. (2)
Определение длительности циклов tД продольно-распиловочных станков, расположенных за головными, на делении заготовок при выполнении технологических операций принято на допущении в постоянстве скорости подачи станков. Действительно, лесоматериалы, пройдя первый уровень обработки на головных станках, приобретают базовые поверхности и стабилизируются по поперечному сечению. На основании этой предпосылки длительность продольного деления заготовки длиной ![]() i для станков проходного типа запишется
i для станков проходного типа запишется ![]() =
= ![]() i/VM, где VM — скорость подачи станка модели М, принимаемая по его паспортной характеристике.
i/VM, где VM — скорость подачи станка модели М, принимаемая по его паспортной характеристике.
Учитывая, что длина лесоматериалов имеет вероятностную природу, функция плотностей случайной величины ![]() будет иметь вид
будет иметь вид
![]() (3)
(3)
Длительность деления заготовки на цикло-проходных станках в математической модели принимается с учетом числа резов np
![]() = np
= np![]() , где
, где ![]() =
= ![]() i/VM(4)
i/VM(4)
Длительность цикла tД определяется с учетом цикловых простоев tД = tℓ + tп. Математическая модель длительности деления заготовок всех видов на готовую продукцию на однопозиционных торцовочных станках базируется на цикловом времени на один рез tlР. Результаты статистической обработки наблюдений за работой торцовочных станков в различных производственных условиях приведены в таблице 2.
Анализ данных таблицы 2 показывает, что параметр цикла tlР описывается, в основном, логнормальным законом с диапазоном изменения среднего значения ![]() = 9 … 16 с и СКО σlР = 2,5 … 6 с. При обслуживании торцовочного станка двумя рабочими, как это имело место в Н–Лялинском цехе, длительность tlР уменьшается примерно в три раза
= 9 … 16 с и СКО σlР = 2,5 … 6 с. При обслуживании торцовочного станка двумя рабочими, как это имело место в Н–Лялинском цехе, длительность tlР уменьшается примерно в три раза
(![]() = 3,18 с, σlР = 0,72 с).
= 3,18 с, σlР = 0,72 с).
Таблица 2
Статистические показатели работы торцовочных станков
|
Цех |
|
σх |
N, шт |
Закон распр. |
Р( |
|
tlР, с ( |
|||||
|
Афанасьевский Камышловский Лобвинский Н-Лялинский Полдневской |
10,95 14,62 9,10 3,18 16,65 |
4,79 5,58 2,52 0,72 6,01 |
322 465 502 506 521 |
эрл лог эрл лог лог лог |
0,34 0,27 0,54 0,16 0,24 0,43 |
Статистические показатели поперечного деления с выполнением операции вырезки дефектных мест принимаются для дальнейших расчетов по литературным данным. Так, время вырезки бракованных участков на сортировке пиломатериалов характеризуется ![]() = 7,76 с и σt = 2,46 с. Время торцовки одной доски —
= 7,76 с и σt = 2,46 с. Время торцовки одной доски — ![]() = 12,4 с, σt = 5,83 с.
= 12,4 с, σt = 5,83 с.
Приведённые математические модели по определению длительности пиления tд реализованы в КПСТАНОККПЦЕХ.
Компонент–программа СТАНОК составлена на основе математических моделей деления лесоматериалов на станках и математических моделей формирования длительностей циклов для станочного оборудования. Схема моделирующего алгоритма приведена на рисунке 1.
Основные входные данные (блок 1): объем моделирования сырья; толщина и длина сырья (среднее, СКО, минимальное и максимальное значения случайных величин, типы вероятностных распределений), породный состав; тип станка и его характеристика; постав; сезон работы; параметры для построения гистограмм. После обнуления сумматоров (блок 2) программа генерирует для каждого i-го бревна породу, толщину di, длину ℓi, определяет объем бревна Vi. В блоке 5 происходит проверка на конец моделирования. При объеме смоделированного сырья ΣV, превышающем заданный объем V![]() , управление передается на блоки 10, 11 для обработки результатов моделирования и выдачи их на печать.
, управление передается на блоки 10, 11 для обработки результатов моделирования и выдачи их на печать.
При ΣV < V![]() управление передаётся к блокам 6, 7, 8 для определения длительности деления i-го бревна на заданном станке. Полученное значение tДiзаносится в соответствующую ячейку (блок 9).
управление передаётся к блокам 6, 7, 8 для определения длительности деления i-го бревна на заданном станке. Полученное значение tДiзаносится в соответствующую ячейку (блок 9).
Выходная информация выдается на печать в виде таблиц, содержащих частоты попаданий значений случайной величины tД в заданные интервалы, а также средние значения и СКО величины tД.
Выбор эффективных головных станков для лесообрабатывающих цехов возможен при сопоставлении их параметров, характеризующих длительность распиловки на них бревен. При принятии в качестве головного станка одноэтажной лесопильной рамы встают вопросы, связанные с рациональными способами распиловки сырья, с его сортировкой на сортировочные группы.
Для лесообрабатывающих цехов, работающих в условиях малообъемных заготовок, приемлемы одноэтажные лесопильные четырехвальцовые и восьмивальцовые рамы. Наиболее распространенной моделью на лесопромышленных предприятиях является рама Р63–4Б. В табл. 3 и на рис. 2 приведены результаты имитационного моделирования лесопильной рамы Р63–4Б по компонент-программе СТАНОК. Как показывают исследования, числовые значения статистических параметров случайной величины tℓ (длительность распиловки бревен на лесопильной раме) зависят от способа раскроя круглых лесоматериалов, параметров распиливаемого сырья и параметров выпиливаемой пилопродукции.
Моделировался раскрой 6-и метрового сырья по ГОСТ 9663–88 для группового деления на пиломатериалы по ГОСТ 8486–66 (постава рассчитывались согласно общей теории раскроя пиловочного сырья с учетом нижних и верхних границ сортировочных групп для сортированного сырья и с учетом dСР ± 2σd для несортированного). Статистики случайной величины tℓ — среднее значение ![]() и среднее квадратическое отклонение σt при распиловке бревен вразвал выше, чем с брусовкой. Так, среднее взвешенное значение
и среднее квадратическое отклонение σt при распиловке бревен вразвал выше, чем с брусовкой. Так, среднее взвешенное значение ![]() при распиловке бревен вразвал (137 … 141 с) на 30 … 50 с выше, чем при распиловке бревен с брусовкой (88 … 110 с). Применение более “тяжелых” поставов при распиловке вразвал по сравнению с более легкими при распиловке с брусовкой дают объяснение этому явлению.
при распиловке бревен вразвал (137 … 141 с) на 30 … 50 с выше, чем при распиловке бревен с брусовкой (88 … 110 с). Применение более “тяжелых” поставов при распиловке вразвал по сравнению с более легкими при распиловке с брусовкой дают объяснение этому явлению.
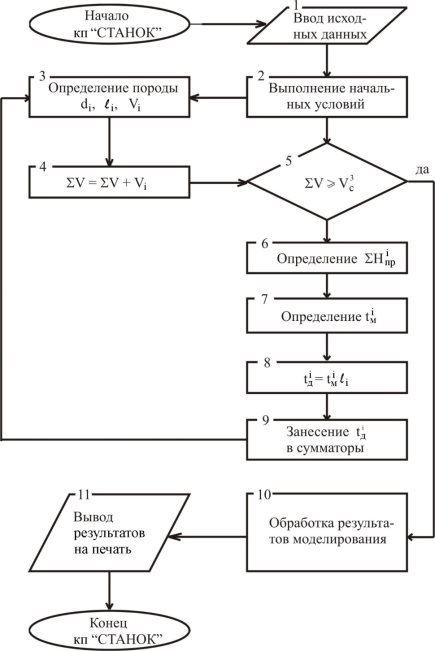
Рис. 1. Принципиальная схема компонент-программы СТАНОК
Сортировка бревен увеличивает длительность их распиловки. При распиловке вразвал несортированного сырья (количество сортировочных групп nСГ=1) ![]() для dСР=20 см по уравнению (1) равно 112 с. Средняя взвешенная длительность распиловки рассортированного на 4-е сортировочные группы сырья (nСГ=4, ∆d=6 см)
для dСР=20 см по уравнению (1) равно 112 с. Средняя взвешенная длительность распиловки рассортированного на 4-е сортировочные группы сырья (nСГ=4, ∆d=6 см) ![]() =137 с, а на nСГ=6 (∆d=4 см) — 141 с. Увеличение длительности распиловки составляет 22…26 %. Приведенные данные имитационного моделирования показывают, что при числе сортировочных групп nСГ= 4–6 значения
=137 с, а на nСГ=6 (∆d=4 см) — 141 с. Увеличение длительности распиловки составляет 22…26 %. Приведенные данные имитационного моделирования показывают, что при числе сортировочных групп nСГ= 4–6 значения ![]() стабилизируются.
стабилизируются.
Таблица 3
Статистические параметры случайной величины tℓ (длительность распиловки бревен на лесопильной раме)
|
Регрессионные уравнения |
Коэф. ур-ний определены при |
№ ур-ний |
|
вразвал из несортированного сырья на необрезные пиломатериалы |
||
|
tℓСР = — 4758,2256 / (- 61,2142 + dСР) |
dСР = 16 … 30 см |
1 |
|
σt= — 49,8130 + 62,7661ℓgdСР |
2 |
|
|
вразвал из 4-х размерно-сортировочных групп сырья с дробностью сортировки ∆d=6 см |
||
|
tℓСР = 0,04167dСР2 + 4,5833dСР + 11,0 |
dСР, см = 16, 22, 28, 34 |
3 |
|
σt = — 0,03320dСР2 + 2,5329dСР — 12,5692 |
4 |
|
|
вразвал из 6-и размерно-сортировочных групп сырья с дробностью сортировки ∆d=4 см |
||
|
tℓСР = 0,09263dСР2 + 1,3612dСР + 60,9185 |
dСР, см = 15, 19, 23, 27, 31, 35 |
5 |
|
σt = — 0,01672dСР2 + 1,5135dСР + 0,6045 |
6 |
|
|
с брусовкой из сортировочно-размерных групп сырья dСГ с дробностью сортировки ∆d=2 см при dСР=20 см |
||
|
tℓСР = 0,1066dСГ2–3,9588dСГ + 120,6301 |
dСГ, см = 14 … 28, 31, 35 |
7 |
|
σt = 0,02133dСГ2–0,7635dСГ + 23,3522 |
8 |
|
|
с брусовкой из сортировочно-размерных групп сырья dСГ с дробностью сортировки ∆d=4 см при dСР=20 см |
||
|
tℓСР = — 0,04688dСГ2 + 3,4509dСГ + 56,7121 |
dСГ, см = 15,19,23,27,31,35 |
9 |
|
σt = — 0,01007dСГ2 + 0,7131dСГ + 10,4922 |
10 |
|
При распиловке бревен с брусовкой значения ![]() ℓС.В. и σt с увеличением количества сортировочных групп сырья уменьшаются. Так, при nСГ=6 и ∆d = 4см
ℓС.В. и σt с увеличением количества сортировочных групп сырья уменьшаются. Так, при nСГ=6 и ∆d = 4см ![]() ℓС.В.=110 с, а при nСГ=10 и ∆d=2см
ℓС.В.=110 с, а при nСГ=10 и ∆d=2см ![]() ℓС.В.=88 с, т. е. на 22 с. Это объяснимо применяемыми поставами. Чем меньше число сортировочных групп, тем больше значения диапазона толщин сырья ∆d в сортировочных группах и, соответственно, количество участвующих в пилении пил.
ℓС.В.=88 с, т. е. на 22 с. Это объяснимо применяемыми поставами. Чем меньше число сортировочных групп, тем больше значения диапазона толщин сырья ∆d в сортировочных группах и, соответственно, количество участвующих в пилении пил.
Общим выводом проведенных исследований следует считать необходимость учета дробности сортировки сырья ∆d при имитационном моделировании технологических потоков лесообрабатывающих цехов. Сортировка бревен, увеличение сортировочных групп уменьшает tℓ и увеличивает пропускную способность станка, но вместе с тем, как известно, увеличивает выход готовой продукции.
Другим значимым фактором, влияющим на длительность распиловки бревен на лесопильной раме, является длина сырья. Для выявления совместного влияния диаметра и длины несортированного сырья был проведен полный факторный эксперимент ПФЭ 22. Значения матрицы были получены имитационным моделированием по кп СТАНОК.
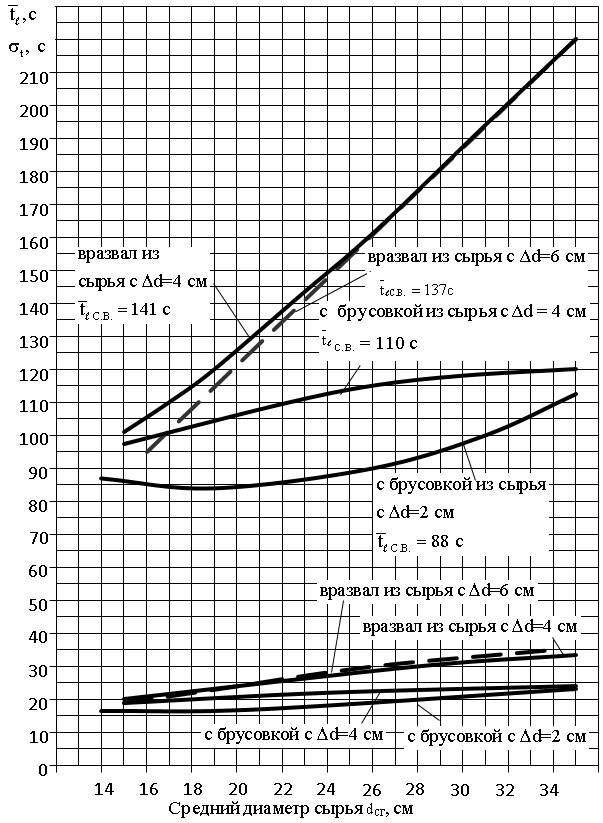
Рис. 2. Статистические параметры случайной величины tℓ в зависимости от способа раскроя круглых лесоматериалов на лесопильной раме и степени дробности сортировки сырья на сортировочно-размерные группы
Математическая модель зависимости средней длительности распиловки бревен на лесопильной раме Р63–4Б от средней толщины dСР и средней длины сырья ℓСР имеет вид ![]() = 2,28dСР + 20,25ℓСР — 53,31, с. [8].
= 2,28dСР + 20,25ℓСР — 53,31, с. [8].
Модель адекватна, соответствует средним условиям dСР=20 см и ℓСР= 6 м с диапазоном варьирования факторов 16,88 ≤ dСР ≤ 23,12 см и 5,5 ≤ ℓСР ≤ 6,5 м.
Таким образом, при выборе станков для технологического процесса лесообрабатывающего цеха необходимо учитывать параметры сырья. Наиболее значимыми из них являются средняя толщина dСР, средняя длина ℓСР, дробность сортировки. Учет дисперсий названных параметров сырья на показатели функционирования станков в технологических потоках возможен на имитационных моделях. Знание влияния параметров сырья на пропускную способность станков позволяет более обоснованно проводить их выбор и (или) назначать для них соответствующее сырье.
Литература:
- Чамеев, В. В. Комплекс-программа ZECH для решения задач анализа и синтеза в лесо-обрабатывающих цехах / В. В. Чамеев, В. В. Обвинцев // ИВУЗ, Лесной журнал.- Архангельск: АГТУ, 1996.- N 4–5.- С. 168–175.
- Чамеев В. В. Управление лесообрабатывающими цехами лесопромышленных предприятий на базе комплекс-программы ZECH / В. В. Чамеев, В. В. Обвинцев, Д. М. Солдатов // ИВУЗ, Лесной журнал. — Архангельск: АГТУ, 2000.- С. 5–6.- С. 36–42.
- Чамеев, В. В. Обоснования технологического процесса лесопильного цеха для малого бизнеса / Чамеев В. В., Еремеев А. А.: УГЛТУ. — Екатеринбург, 2011.- 72 с. Деп. в ВИНИТИ 28.03.11, N 146-В2011.
- Чамеев В. В. Методология исследования и проектирования технологических процессов лесообрабатывающих цехов по выработке пилопродукции / В. В. Чамеев, А. А. Еремеев // Леса России и хозяйство в них: жур. Вып. 2(32) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2009. — С. 64–71.
- Редькин, А. К. Математическое моделирование и оптимизация технологий лесозаготовок: учебник для вузов/ А. К. Редькин, С. Б. Якимович. — М.: ГОУ ВПО МГУЛ, 2005.-504 с.
- Советов, Б. Я. Моделирование систем: Учебник для вузов.- 3-е изд., испр. и дополн. /Б. Я. Cоветов, С. А. Яковлев. — М.: Высшая школа, 2003.-343 с.
- Чамеев, В. В. Обзор исследований по основным параметрам и операциям в лесообрабатывающих цехах / В. В. Чамеев, А. А. Еремеев // Леса России и хозяйство в них: жур. Вып. 2(32) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2009.- С. 61–64.
- Чамеев, В. В. Планирование экспериментов на имитационных моделях комплекс-программы«ЦЕХ» / В. В. Чамеев, К. В. Ивачёва, Р. А. Уксусов, В. В. Терентьев // Леса России и хозяйство в них: жур. Вып. 1(44) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2013. — С. 104–107.







