Исследование закономерности размерно-качественных параметров сортиментов



Исследование закономерности размерно-качественных параметров сортиментов

Чамеев Василий Владимирович, кандидат технических наук, доцент;

Солдатов Александр Владиславович, кандидат технических наук, доцент;

Иванов Виктор Вячеславович, кандидат технических наук, доцент;

Букрин Сергей Игоревич, студент;

Деменев Артем Дмитриевич, студент;

Подольский Ян Александрович, студент

Уральский государственный лесотехнический университет

Приведены математические модели размерно-качественных параметров круглых лесоматериалов.

Одной из основных задач изучения круглых лесоматериалов, как предмета труда, является выявление закономерностей, по которым можно было бы находить размерные характеристики круглых лесоматериалов, получаемых в процессе раскряжёвки хлыстов.

Круглые лесоматериалы укрупнённо характеризуются породным составом и сортностью. К размерным параметрам сырья относятся толщина, длина и сбег, к основным качественным его параметрам, влияющим на сортность, — гниль, кривизна и сучки. Перечисленные параметры сырья являются случайными величинами и обладают большой вариацией.

Толщина круглых лесоматериалов занимает основное место в статистической модели сырья, являясь, с одной стороны, доминирующим фактором для описания сортообразующих пороков сырья и, с другой стороны, завися от многих факторов. Анализ толщины сырья, выполненный исследователями, показывает, что на нее влияют средний объем хлыста, породный состав сырья, сортиментная структура и наличие лесообрабатывающих цехов на предприятии, другие природно-климатические и производственные факторы.

Толщина круглых лесоматериалов, как случайная величина, характеризуется средним значением , средним квадратическим отклонением (СКО) σ_d и описывается вероятностным законом.

Средние значения толщин сырья , поступающего в лесообрабатывающие цехи, как показывают исследования, не постоянны даже в течение небольшого календарного периода времени. Коэффициент вариации значений вокруг общей средней составляет 8–11 %. Величина является случайной и ее можно представить в виде определенной функции плотностей f(), у которой среднее значение равно , а СКО (0,08–0,11) [1].

Наибольшее значение по толщине из лиственных пород (берёза и осина) для Среднего Урала имеет осина. Она толще березы на Δ = 1,5- 6,6 см [1]. При решении задач, связанных с попородной сортировкой круглых лесоматериалов, необходимы данные о средних толщинах сырья по породам при известном их общем среднем . Для случая двух пород из очевидных выражений

= P_{oс oс} + P_{б б}, Р_ос + Р_б = 1,

где Р_ос и Р_б — доля бревен осины и березы в выборке; _ос и _б — средние значения их толщин, имеем

_ос = + ΔР_б, _б = - ΔР_ос.

При известных _ос и _б решается и обратная задача — определение значений в зависимости от соотношения Р_б/Р_ос.

Доля бревен комлевой вырезки в выборках во времени непостоянна. Вокруг общего среднего значения _кв она варьирует на 12,8 %. Круглые лесоматериалы по толщине с учетом породы и места вырезки из хлыстов распределяются по вероятностному закону. Круглые лесоматериалы из комлевой части хлыстов на 3,4–6,2 см толще, чем из вершинной и серединной. Между толщиной бревен d_i и долей бревен комлевой вырезки _кв существует связь [1]:

_кв = — 0,0006 d²_i + 0,0552 d_i — 0,586.

Здесь d_i — отдельные значения случайной величины d. Полученное уравнение действительно для условий Среднего Урала в диапазоне 14 ≤ d_i ≤ 46 см, необходимо для решения ряда задач, связанных с сортировкой круглых лесоматериалов по месту вырезки из хлыстов, определения протяжённостей гнилей и т. д.

1. Зависимость толщины сортиментов от объёма хлыстов [2, 3, 4, 5].

Уравнение связи между средними диаметрами сортиментов и средним объёмом хлыста V имеет вид:

,

где ℓ — средняя длина деловых и дровяных сортиментов;

для пиловочных бревен

,

где ℓ — средняя длина деловых сортиментов.

В приведенных уравнениях диаметры выражены в сантиметрах, длина — в метрах.

Первое уравнение действительно при 0,18 ≤ V ≤ 1,88 м³ и 1,3 ≤ ℓ ≤ 6,3 м; второе при 0,18 ≤ V ≤ 2,05 м³ и 2,1 ≤ ℓ ≤ 6,5 м. Дальнейший анализ показал, что длина сортиментов мало влияет на величину . В табл. 1 и на рис. 1 приведены зависимости =f(V) для сортиментов и их групп.

Таблица 1

Средние значения распределений сортиментов по диаметрам

Сортименты иих группы	Уравнения	Уравнения действительны при V, м3
Деловые и дрова Деловые Дрова Пиловочник Пиловочник экспортный Шпальный кряж Технологические дрова Дрова и технологическое сырьё	= е3,156 V0,394 = е3,179 V0,500 = е3,154 V0,395 = е3,260 V0,410 = е3,248 V0,250 = е3,299 V0,304 = е3,510 V0,113 = е3,202 V0,360 = е3,250 V0,405	0,18–0,9 0,9–1,88 0,18–2,05 0,18–1,88 0,18–2,05 0,32–1,88 0,47–2,05 0,51–1,88 0,18–1,88

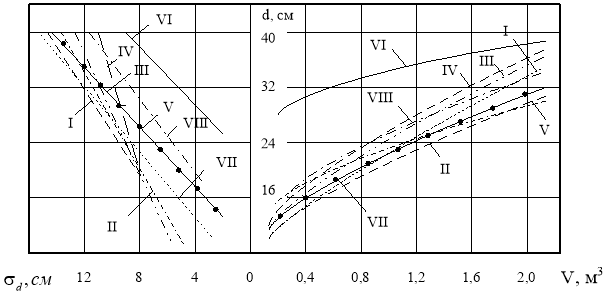
Рис. 1. Зависимость среднего диаметра сортиментов от среднего объёма хлыста и среднеквадратического отклонения от среднего диаметра сортиментов [5]: I — деловых и дровяных; II — деловых; III — дров и технологических дров; IV — дров; V — пиловочника; VI — шпального кряжа; VII — технологических дров; VIII — пиловочника экспортного

2. Зависимость среднего квадратического отклонения от толщины сортиментов [2, 3, 4, 5, 6].

Мерой рассеяния отдельных значений вокруг среднего значения случайной величины служит среднее квадратическое отклонение. Исследованиями установлено, что между средним квадратическим отклонением σ_d случайной величины d (толщина сортимента) и средним значением существует статистическая зависимость. Зависимость σ_d = f() для сортиментов и их групп приведена в табл. 2 и на рис. 2 и 3.

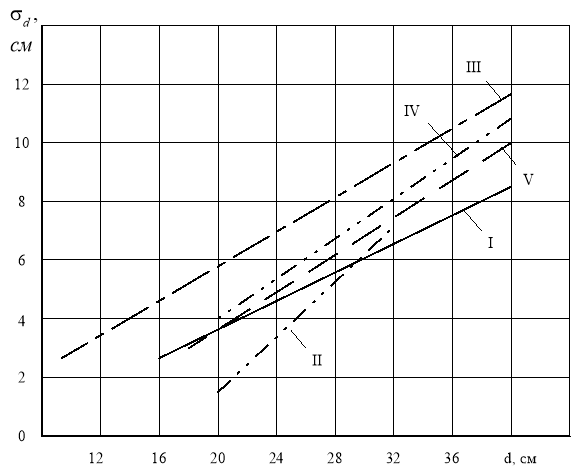
Рис. 2. Зависимость среднего квадратического отклонения от среднего диаметра сортиментов [5]: I — фанерного; II — лыжного; III — тарного; IV — спичечного; V — клёпочного

Аналогичные зависимости получены для сырья лесообрабатывающих цехов Среднего Урала [6, 1]:

, .

Графическая иллюстрация представлена на рис. 3. Для построения зависимостей изучались потоки сортиментов к технологическим потокам лесообрабатывающих цехов (лесопильных, тарных, комбинированных лесопильно-тарных) с групповым (Гр) раскроем сырья на головных станках (лесопильные одноэтажные рамы, ФБС, спаренные ленточно-пильные станки и др.) и индивидуальным (И) раскроем (круглопильные и ленточно-пильные с кареткой).

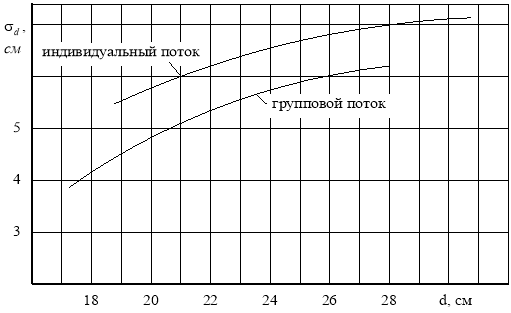
Рис. 3. Вид зависимостей σ_d = f() [1]

Таблица 2

Среднее квадратическое отклонение распределений сортиментов по диаметрам

Сортименты иих группы	Уравнения	Уравнения действительны при , см
Деловые и дрова Деловые Дрова Пиловочник Шпальный кряж Пиловочник экспортный Технологические дрова Дрова и технологическое сырьё Фанерный кряж Лыжный кряж Тарный кряж Спичечный кряж Клёпочный кряж	σd = 0,30749 + 1,92526 σd = 0,28994 + 2,04981 σd = 0,17571 + 4,43257 σd = 0,43961 — 3,50189 σd = 0,47327 — 10,39659 σd = 0,38114 — 3,43571 σd = 0,42111 — 1,19282 σd = 0,21879 + 3,75257 σd = 0,23836 — 0,97993 σd = 0,57863 — 10,06687 σd = 0,29513 — 0,18693 σd = 0,35029 — 3,24226 σd = 0,31383 — 2,67269	11,3–36,8 12,3–36,5 11,0–38,6 16,2–40,5 29,6–38,2 20,3–39,5 10,9–38,5 12,1–41,2 17,2–43,2 22,1–27,7 15,7–35,7 22,0–35,0 18,1–44,9

Круглые лесоматериалы для Гр-раскроя характерны для лесопильных потоков и цехов малой мощности и для технологических потоков тарных цехов с одноэтажными лесопильными рамами (в основном пиловочник). Сырьё для И-раскроя относится только к тарным цехам (в основной массе низкосортное сырьё с некоторым содержанием сырья для технологической переработки).

3. Распределение сортиментов по толщине.

Помимо среднего значения и среднего квадратического отклонения, толщина сортиментов описывается вероятностными законами. При анализе эмпирических распределений круглых лесоматериалов по толщине рядом исследователей [2, 3, 4] замечено, что при малых средних значениях толщины кривые распределений асимметричны, а с увеличением они становятся более симметричными, приближаясь к нормальным. В этой связи за гипотетические законы при описании толщины сырья приняты нормальный и логарифмически нормальный [1].

Однако четкой границы перехода логарифмически нормального распределения при увеличении в нормальное не обнаружено. Следовательно, о математическом описании толщины круглых лесоматериалов с конкретным значением в этой переходной зоне нормальным или логарифмически нормальным законом следует говорить с определенной вероятностью.

Ранжирование результатов статистической обработки эмпирических распределений позволяет найти вероятность описания распределения случайной величины d логарифмически нормальным законом Р_лог в зависимости от . Тогда вероятность описания случайной величины нормальным законом составит Р_нор = 1 — Р_лог.

Графическая иллюстрация зависимостей Р_лог = f () и Р_нор=f() приведена на рис. 4. Приведённые графики зависимостей для Гр- и И-потоков круглых лесоматериалов по особенностям деления на головных станках различны. Функцию плотностей распределения случайной величины d можно записать в виде

[1 / (σd)]exp{– 0,5 [(lnd — a) /σ]²}

[1 / (σ_d)]exp{– 0,5 [(d — ) / σ_d]²},

где a и σ — параметры логарифмически нормального распределения, численно равные:

a = ln- 0,5 ln(1 +σ_d / ²); σ² = 2 ln- 2 a.

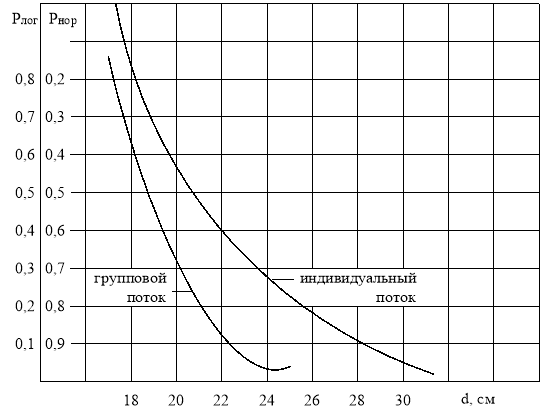
Рис. 4. Вероятность описания толщины круглых лесоматериалов логарифмически нормальным и нормальным законами [1]

Вероятность описания случайной величины d логарифмически нормальным законом равна:

Р^гр_лог = 1 для группового потока при до 16,2см;

Р^гр_лог = 0,0117^2–0,6032+ 7,7102 при 16,2 см < ≤ 25 см;

Р^и_лог = 1 для индивидуального потока при до 17,7 см;

Р^и_лог = 0,0056 ^2–0,3500 + 5,4346 при 17,7 см < ≤ 31 см.

Нормальным законом толщина сырья d описывается с вероятностью: для группового потока:

Р^гр_нор = 1 — Р^гр_лог, при 16,2 см < ≤ 25 см;

Р^гр_нор = 1 при d > 25 см;

для индивидуального потока:

Р^и_нор = 1 — Р^гр_лог, при 17,7 см < ≤ 31 см;

Р^и_нор = 1 при > 31 см.

Ряд авторов [2, 3, 4] установили, что распределение круглых лесоматериалов по толщине не противоречит закону распределения размахов, интегральная функция которого имеет вид: .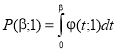

Плотность распределения равна:

,

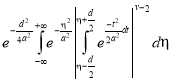где v и а — параметры закона распределения.

Параметр v определяет порядок закона распределения, в котором β = d/a.

Значения функции и плотности распределения табулированы. На основании формул и таблиц можно определить вероятность нахождения значений толщины d в произвольно заданном интервале. На основании полученных зависимостей в соответствии с формулами закона распределения размахов разработана система графиков (рис. 5 и 6), по которым можно определить вероятность того, что при раскряжёвке хлыстов определённого объёма будут получены круглые лесоматериалы соответствующего диаметра.

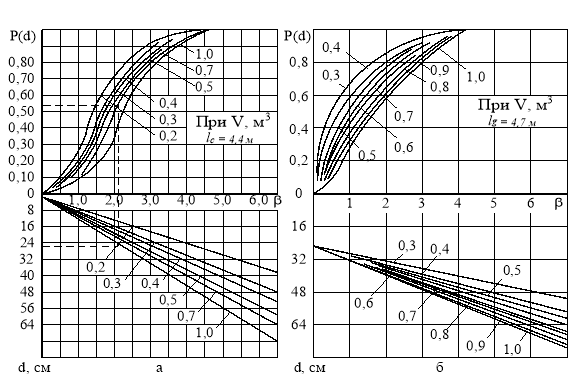
Рис. 5. Функция распределения сортиментов по ступеням толщины в зависимости от среднего объёма хлыста и средней длины сортиментов [2]: а — все сортименты; б — пиловочник

Порядок определения толщины круглых лесоматериалов на графиках указан пунктирными линиями.

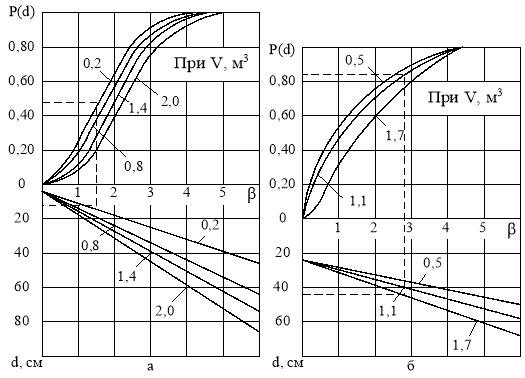
Рис. 6. Функция распределения сортиментов по ступеням толщины в зависимости от среднего объёма хлыста: а — дрова; б — шпальный кряж [2]

4. Эллиптичность сечения круглых лесоматериалов [2, 3, 7, 8].

Эллиптичность сортиментов учитывают при определении объёмного выхода пиломатериалов [7, с. 257], при этом указывается, что теоретически из эллиптических брёвен можно получить пиломатериалы с таким же объёмным выходом, что и из брёвен круглого сечения. Основным параметром, характеризующим эллиптичность, является средняя величина эллиптичности Δ. Основным фактором, влияющим на величину Δ, является средняя толщина (диаметр) круглых лесоматериалов. На среднее квадратическое отклонение σ и коэффициент вариации V разностей между наибольшим и наименьшим диаметрами поперечных сечений круглых лесоматериалов основное влияние оказывает среднее значение эллиптичности Δ:

= 0,047 — 0,169 при 28 ≤ ≤ 43;

σ = 0,223 + 0,865 при 1,16 ≤ ≤ 2,01;

V = + 9,963 при 1,16 ≤ ≤ 2,01.

Для шпальных кряжей [8, с. 8] из сосны = 0,23 + 0,025d, из ели = 0,04 + 0,035d.

Распределение разностей наибольших и наименьших значений поперечных сечений круглых лесоматериалов может описываться формулами закона распределения размахов.

5. Параметры коры усортиментов.

В практике разработки, выбора лесообрабатывающих машин, в технологических расчётах возникает необходимость в данных по коре. В работе [2, с. 101] предлагается формула для определения диаметра бревна в коре d_к, см:

d_к = 10d_бк,

где d_к и d_бк — диаметры бревна в коре и без коры на середине сортимента, см; К — объём коры, % от объёма бревна.

К = ,

где V_к и V_бк — объёмы бревна с корой и без коры, м³.

Зависимость толщины коры h_к от диаметра бревна d представлена на рис. 7 [4].

Регрессионные зависимости h_к = f(d) имеют вид [8, с. 8]:

для ели h = 0,0022d² + 0,025d + 2,7,

для сосны вершинной части ствола h = 0,003d² + 0,01d + 1,1,

для сосны комлевой части ствола h = 0,0105d² + 0,15d + 2,0,

где h — толщина коры, мм, d — диаметр бревна, см.

Для остальных пород — в трудах ЦНИИМЭ № 41 за 1963 г.

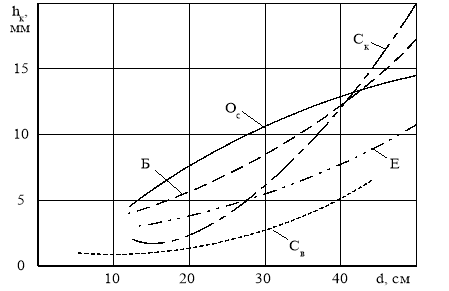
Рис. 7. Зависимость толщины коры h_к от диаметра бревна d: Б — для берёзы; О_с — для осины; Е — для ели; С_к — для сосны (комлевое бревно); С_в — для сосны (вершинное бревно)

6. Распределение сортиментов по длинам [2, 3].

В процессе раскряжёвки древесный хлыст делится на отрезки разной длины (сортименты). Длина сортиментов обусловливается различными причинами (наличием пороков и расположением их по хлысту, сортиментным планом, наличием перерабатывающих производств, действующими стандартами).

Распределение круглых лесоматериалов по длинам на примере некоторых сортиментов, отгружаемых лесопромышленными предприятиями потребителю, приведены в табл. 3 [9].

Таблица 3

Распределение по длинам круглых лесоматериалов, поставляемых ввагонах,%

Сортименты	Длина, м
	Менее 2	2–2,9	3–4,4	4,5–6,5	6,5 иболее
Пиловочник: − хвойный − лиственный Тарное сырьё	— 0,1 28,6	— 1,4 17,6	70 74,8 45	28 20 8,8	2 3,7 —

Для групп длин сортиментов установлены зависимости Р_i = f(l_c), где Р_i — доля сортиментов (шт.) определённой группы по длине в общем их количестве, %; l_c — средняя длина круглых лесоматериалов, м. Результаты приведены в табл. 4.

Таблица 4

Зависимость доли группы сортиментов определённой длины

Диапазон длин сортиментов	Уравнения	Уравнения действительны при lc, м
До 2 м 4,1–6,5 м Более 6,5 м	Р1 = Р2 = Р3 =	2,2 < lc < 5,3 2,2 < lc < 6,4 2,2 < lc < 6,4

На основании полученных зависимостей разработана диаграмма (рис. 8), по которой можно определить вероятность получения круглых лесоматериалов определённой группы длин при известной средней длине всех лесоматериалов. Порядок определения групп для круглых лесоматериалов указан сплошными линиями, характеристика точек, изображённых на диаграмме, приведена в табл. 5.

Например, при средней длине круглых лесоматериалов 3 м (точка 1) распределение количества круглых лесоматериалов по группам длин будет следующее: до 2 м включительно — 41,6 %, с 2,1 до 6,5 м — 57,6 %, более 6,5 м — 0,7 %.

Длина круглых лесоматериалов, поступающих в лесообрабатывающие цехи, распределяется по нормальному закону. Распределения длины сырья могут быть и полимодальными. Такие ситуации возникают в случаях, когда в цех поступает сырьё нескольких назначений. В общем виде статистическая модель сырья по длине запишется в виде [1]

[1/(σ_е1)] exp {-0,5 [(l-_i)/σ_еi]} с вероятностью Р_i;

f(l) = [1/(σ_еi)] exp {-0,5 [(l-_j)/σ_еi] } с вероятностью Р_j;

[1/(σ_еn)] exp {-0,5 [(l-_n)/σ_еn] } с вероятностью Р_n,

где и - среднее значение длины сырья и его СКО для j-й группы по длине; P_i — вероятность появления j-й группы по длине ().

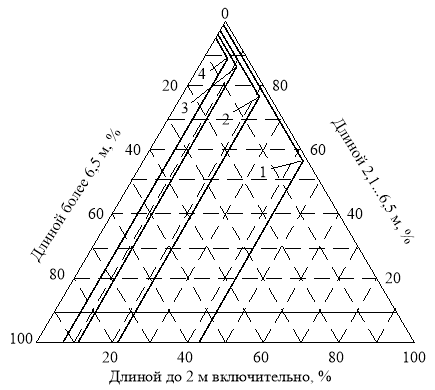
Рис. 8. Распределение сортиментов по группам длин

Таблица 5

Характеристика точек на диаграмме рис. 8

Номер точки	Средняя длина сортиментов, м	Группа длин, м
		До 2	2,1–6,5	Более 6,5
1 2 3 4	3 4 5 6	41,6 23,1 12,4 5,3	57,7 74,8 84,5 89,7	0,7 2,1 3,1 5,0

Параметры приведенной модели для некоторых лесоперерабатывающих цехов приведены в табл. 6 (по данным кафедры ТиОЛП УГЛТУ).

Анализ данных, приведенных в табл. 6 позволяет выявить тенденцию уменьшения с увеличением . Коэффициент вариации V, характеризующий разброс длин, может быть и выше. По данным работы [10], значение V у низкокачественного сырья достигает 27–28 %.

Таблица 6

Результаты статистической обработки данных по длине круглых лесоматериалов, поступающих влесоперерабатывающие цехи

Цех	Закон распределения		, см	, см	V, %	Pi
Лобвинский Полевской Афанасьевский Баяновский Щ-Озерский Талицкий	нормальный	0,16 0,31 0,24 0,43 0,33 0,19 0,74 0,68	198,38 253,88 243,81 400,53 399,80 205,92 254,77 303,79	16,81 13,52 13,44 9,97 7,35 9,25 6,43 3,16	8,47 5,33 5,51 2,49 1,81 4,49 2,52 1,04	1 1 1 1 1 0,166 0,606 0,228

7. Сбег.

Значения сбега оказывают большое значение на выход готовой продукции. У бревен средней длины (6 м) на зону сбега падает 20,8 %, у длинных (10 м) — 31 % объема бревен. Объем сбеговой зоны у тонких бревен больше, у толстых — меньше. Так, при длине бревен 6 м и толщине 15 см зона сбега составляет 24,2 % объема бревен, при толщине 25 см той же длины — 19,4 и при толщине 40 см — 16,7 % [11, с. 27–28].

Объемы бревен любых диаметров и длин вычисляются по формуле, интерпретирующей таблицы ГОСТ 2708–75.

V = (0,87L+0,01L²)(d+0,0001L²)²+0,0000L³, м, (*)

где d — вершинный диаметр бревна, м; L — длина бревна, м.

Сбег бревен характеризуют два показателя: коэффициент сбега K и сбег S.

;

,

где D — комлевой диаметр (ввиду наличия в нижней части бревен корневых наплывов численное значение D у комлевых бревен берется отступя от комлевого торца бревна на 1 м), см; d — вершинный диаметр, см; L — длина бревна, м (для комлевых бревен L — 1).

Сбег колеблется в значительных пределах в зависимости от толщины бревен, породы, условий и места произрастания древесных стволов (бонитета). При вычислении сбега бревен принимают во внимание геометрическую форму бревен. Отдельные части ствола приближаются по геометрической форме к нейлоиду, цилиндру, усеченному параболоиду вращения второго порядка или к конусу [12, с. 21].

При принятии формы бревен в виде усеченного параболоида вращения сбег выражается формулой [13, с. 22]

,

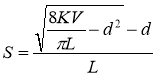где V — объем бревна, вычисленный по формуле (*), м³; K — коэффициент, учитывающий поправку на увеличение объема бревен диаметром 0,14 и 0,16 м в зависимости от содержания в них сильносбежистых вершинных сортиментов (для бревен других диаметров этот коэффициент принимается равным 1).

При подготовке исходной информации для расчета поставов значения коэффициента K берутся из табл. 7.

Определение величины сбега S, см/м, зависимости от вершинного диаметра пиловочных бревен, их длины и бонитета возможно по формуле Титкова Г. Г.:

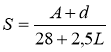
где d — вершинный диаметр, см; L — длина бревен, м; А — коэффициент, принимаемый по табл. 8.

Таблица 7

Значения поправочного коэффициента К [13, с. 22]

Кол-во вершинных сортиментов на 100 бревен	Значения Kдля бревен диаметром, м		Кол-во вершинных сортиментов на 100 бревен	Значения Kдля бревен диаметром, м
	0,14	0,16		0,14	0,16
10 20 30 40 50	1,026 1,052 1,078 1,104 1,130	1,011 1,020 1,030 1,041 1,053	60 70 80 90 100	1,156 1,182 1,208 1,234 1,260	1,067 1,083 1,101 1,121 1,143

Таблица 8

Значения коэффициента А

Бонитет	Ia	I	II	III	IV	V
A	10	15	20	25	30	35

В лесопилении уточненные средние сбеги, свойственные наиболее распространенным в России насаждениям II и III бонитетов приняты в размерах, приведенных в табл. 9 (по Титкову Г. Г.)

Таблица 9

Уточнённый средний сбег Sдля II иIII бонитетов [11, с. 27]

Диаметр бревен вверхнем отрезе, см	S, см/м	Диаметр бревен вверхнем отрезе, см	S, см/м
12–13 14–18 19–22 23–26 27–30 31–34 35–38	0,75 0,80 0,90 1,00 1,10 1,15 1,25	39–42 43–46 47–50 51–55 56–58 60 и более	1,35 1,45 1,55 1,65 1,70 1,80

При использовании табл. 9 необходимо учитывать, что действительные сбеги будут распределяться по закону нормального распределения и иметь отклонения. В табл. 10 представлены среднеарифметические величины среднего сбега и среднеквадратические отклонения от него для бревен разной толщины.

Таблица 10

Значения среднего сбега ипоказатели его вариации [11, с. 26]

D,* см	Средний сбег, в см	Среднее квадратическое отклонение, см	Коэффициент вариации, в%
15 20 25 30 35 40 45 50 55	0,77 0,84 0,89 0,94 1,06 1,18 1,37 1,67 1,87	0,34 0,32 0,29 0,27 0,32 0,37 0,36 0,63 0,87	44,4 38,1 32,6 28,7 31,9 31,4 26,3 38,3 47,5
Среднее	0,96	0,38	38,5

* — диаметр, для комлевых брёвен на расстоянии от комля 1 м, для всех остальных — в нижнем торце

Табличная иллюстрация зависимости среднего сбега от длины брёвен приведена в табл. 11.

Таблица 11

Значения нормального сбега [14]

Толщина бревна вверхнем отрезе, см	Нормальный сбег, см/м
	3–4,5	5–8	8,5 и более
До 16 см 16–27 28–36 37–46 47 и более	1,0 1,5 2,0 2,5 3,0	0,75 1,10 1,25 1,5 2,0	0,50 0,75 1,00 1,25 1,50

В работе [15] даны значения сбега и встречаемость бревен с разным коэффициентом сбега для пиловочных бревен пород, характерных для Сибири и Дальнего Востока, в зависимости от диаметра и места вырезки из хлыста (комлевые, серединные и вершинные).

В технической литературе имеются и другие подходы к математическому описанию сбега. Так, в работе [3] приведена формула для определения непосредственно не сбега, а сразу толщины нижнего торца бревна:

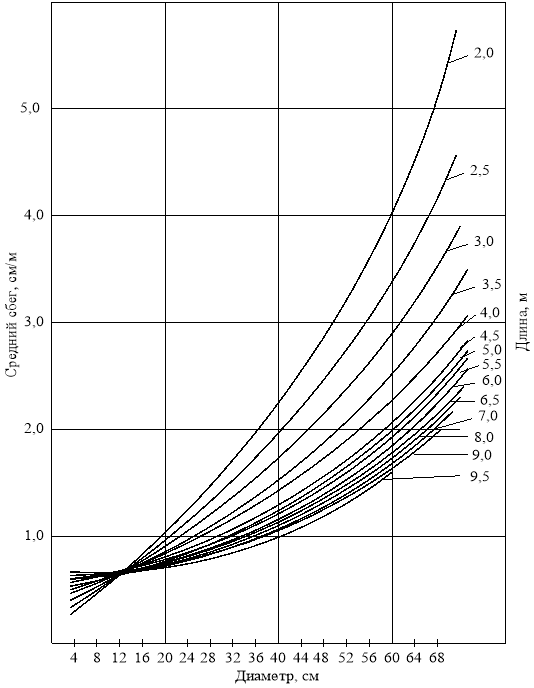
Рис. 9. Зависимость среднего сбега круглых лесоматериалов от их толщины [4]

,

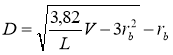где V — объем бревна, м³; L — длина бревна, м; r_b — радиус верхнего торца бревна, м.

В работе [16, с. 134] находим

.

Для шпальных кряжей проведены отдельные исследования по сбегу [8, с. 8]:

для ели S=0,632 + 0,034d, см/м;

для сосны S=0,01 + 0,04d, см/м,

где d — диаметр верхнего торца кряжа, см. В табличной форме сбег шпальных кряжей приведен в [17, с. 14–17; 19, с. 23].

Для низкокачественных бревен лиственных пород, характерных для европейской части России, значения, характеризующие сбег, несколько иные. Для березы при d_cp = 20,4 см S = 1,38 см/м; средние квадратические отклонения = 0,76 см/м; коэффициент вариации V = 55 %. Соответственно для осины: при d_cp = 23,7 см S = 0,87 см/м, = 0,52 см/м, V = 59 %. Данные приведены из источника [10] для 3-х метровых бревен.

В графической форме средний сбег круглых лесоматериалов представлен на рис. 9.

На основании сопоставления различных материалов по сбегу, приведенных выше, определение величины сбега Si возможно по статистической модели вида

где = (A + d)/(28 + 2,5L); =0,40–0,60 .

8. Породный состав [1].

Значительный удельный объем обработки в лесообрабатывающих цехах занимают лиственные породы. Из лиственной породы преобладающей породой является береза, доля которой в породном составе лиственного сырья составляет 55–88 %.

Колебание породного состава сырья по сменам изучено на примере двух цехов (Лобвинского и Камышловского). Коэффициент вариации, характеризующий колебание отдельных пород на протяжении 21-й смены, различен. Замечено, чем меньше удельный вес j-й породы в составе сырья, тем больше её вариация V и наоборот. Лиственные породы, составляющие основу сырья, имеют V до 40 %, а хвойные — 88–100 %. Из лиственных пород у березы, имеющей наибольший удельный вес в составе лиственного сырья, V равен 25–34 %, а у осины 40–44 %.

Тогда, приняв колебание i-й породы в составе сырья по нормальному закону, на основании полученных данных статистическая модель породного состава запишется в виде f(P_л) = [1/ (σ_л)] exp {- 0,5 [(P_л — _л)/σ_л]²},

где σ_л = 0,01–0,40 _л.

Р_xi = 100 — Р_лi.

f(P_б) = [1/ (σ_δ)] exp {- 0,5 [(Р_б -_б)/σ_δ]²},

где σ_δ = 0,25–0,34_б.

Р_ос = 100 — Р_бi.

Функция плотностей f(P_л) может быть использована для моделирования отдельных значений процентного состава лиственных пород Р_л1, Р_л2,..., Р_лi для отдельных смен. Тогда процентный состав хвойных пород для смоделированной смены составит

Р_хi = 100 — Р_лi.

Аналогично и функция плотностей f(Р_б), только для моделирования процентного состава бревен березы и осины, т. е. Р_бi и Р_осi находятся для i-й смены.

9. Встречаемость сортиментов сгнилью и распределение гнилей [18, 1].

Исследовалась встречаемость бревен с гнилью Р_г, в том числе со сквозной Р_гс, степень поражения гнилью торцов бревен в долях их толщины d_г/d (среднее _г/d, стандарт σ(d_г/d), закон распределения).

Перечисленные характеристики гнили исследовались попородно для технологических потоков по И- и Гр-делению круглых лесоматериалов. Основным фактором, влияющим на численные значения параметров гнили, является d_i. По полученным статистическим данным определены уравнения связи Р_г = f(d_i), Р_гс = f(d_i), _г/d = f(d_i) и σ(d_г/d) = f (d_i), представленные в табл. 12. Сравнение фактических значений критерия Фишера и табличных показывает, что в уравнениях табл. 12: (2), (3), (6), (12), (16) и (19) найденные статистические связи следует считать приближенными, поскольку они соответствуют более высокому 5 процентному уровню значимости.

Для таких случаев дополнительно дана размерная характеристика сырья гнили для двух градаций сырья по толщине — средних толщин и толстомерного, как и для условий ограниченного числа наблюдений (уравнения табл. 3.12: (8'), (20'), (21'), (22'), (23') и (24').

Графический анализ полученных результатов позволяет сделать следующие выводы.

Встречаемость бревен с гнилью Р_г и Р_гс возрастает с увеличением d_i. На технологические потоки по И-делению круглых лесоматериалов поступает сырье с большой долей бревен с гнилью, чем на потоки с Гр-делением. Различия по численным значениям Р_г и Р_гс в березовом и осиновом сырье И-потока несущественные, но их следует учитывать в потоках по групповому делению.

Параметр торцовой гнили _г/d с изменением d_i у осины, особенно предрасположенной по своим биологическим свойствам к загниванию, увеличивается значительно в большей степени, чем у березы. Величина роста _г/d зависит от назначения сырья. Для потоков с И-делением он выше, чем у сырья, предназначенного к делению Гр-способом. У березы и осины для Гр-деления в тонкомерном сырье и сырье средних толщин, а также березы для И-деления на тех же толщинах значения _г/d практически остаются неизменными.

Таблица 12

Содержание бревен сгнилью иразмерная характеристика торцовой гнили от толщины сырья

Поток	Порода	Регрессионные уравнения	Fф	F0.05	Коэф. .ур-ний определены при di, см	№уравнения
1	2	3	4	5	6	7
Гр Гр Гр Гр Гр Гр Гр Гр	Б Б Б Б Б Б Б Б	Рг = 0,0008d2i-0,0327di+0,3981 Pгc = 0,0006 d2i -0,0266 di +0,5087 Pгc = 0,274 Pгc = 0,310 dг/d = 0,0002d2i -0.0062di +0,4438 dг/d = 0,390 dг/d = 0,399 σ(dг/d) = 0,0003d2i+0,0132di +0,0348	3,8 2,1 — — 2,0 — — 2,6	1,79 2,30 — — 2,46 — — 2,46	14–36 15–35 ≤25 ≥26 15–31 ≤25 ≥26 15–27	(1) (2) (2') (2') (3) (3') (3') (4)
Гр Гр Гр Гр Гр Гр Гр	Ос Ос Ос Ос Ос Ос Ос	Pг = 0,0006d2i -0.0096 di+0.2703 Pгc = 0,0024d2i-0,0692di +0,8521 Pгc = 0,281 Ргс = 0,464 dг/d = 0,0003d2i-0.0103di +0,5930 σ(dг/d) = 0,178 σ(dг/d) = 0,142	4,9 1,0 — — 2,7 — —	1,73 2,28 — — 2,28 — —	12–38 15–35 ≤25 ≥26 15–35 ≤25 ≥26	(5) (6) (6') (6') (7) (8') (8')
И И И И И И	Б Б Б Б Б Б	Рг= -0,0005d2i +0,0473di -0,2254 Ргс= -0,0003d2i +0,0362di -0,1636 r/d = 0,00006d2i-0,0011di +0,3897 σ(dг/d) = 0,00003d –0.0027di +0,2038 σ(dг/d)= 0,168 σ(dг/d) = 0,156	49,5 13,4 1,8 1,2 —	1,64 1,66 1,67 1,67	10–42 10–40 12–40 12–40 ≤25 ≥26	(9) (10) (11) (12) (12') (12')
И И И И И И	Ос Ос Ос Ос Ос Ос	Рг = -0,0005d2i+0,0511di-0,2392 Ргс = -0,00002d2i+0,0190di+0,0303 r/d = 0,00002d2i-0,0033di+0,4834 σ(dг/d)= 0,00003d2i-0,0006di +0,1645 σ(dг/d) = 0,159 σ(dг/d) = 0,179	34,7 4,2 4,1 1,1 — —	1,64 1,66 1,66 1,66 — —	10–42 12–42 12–40 12–42 ≤25 ≥26	(13) (14) (15) (16) (16') (16')
И И И И И И И	С С С С С С С	Рг = 0,0007d2i-0,0264di +0,3452 Ргс =0,00005d2i+0,0058di +0,0063 r/d = -0,0002d2i+0,0093di +0,4371 r/d = 0,559 r/d = 0,581 σ(dг/d) = 0,196 σ(dг/d)= 0,228	3,3 7,5 1,8 — — — —	1,69 2,30 2,70 — — — —	14–40 15–35 15–27 ≤25 ≥26 ≤25 ≥26	(17) (18) (18) (19') (19') (20') (20')
И И И И И И И И	Лп Лп Лп Лп Лп Лп Лп Лп	Рг = 0,581 Рг = 0,912 Ргс = 0,500 Ргс = 0,615 г/d = 0,474 г/d = 0,502 σ(dг/d) = 0,175 σ(dг/d) = 0,158	- — — — — — — —	- — — — — — — —	≤25 ≥26 ≤25 ≥26 ≤25 ≥26 ≤25 ≥26	(21') (21') (22') (22') (23') (23') (24') (24')

Осина имеет большую пораженность торцов гнилью, чем береза. В березовом сырье значения _г/d одинаковы как для И-, так и для Гр-потоков, а в осиновом сырье, предназначенном для И-потока, степень пораженности торцов гнилью больше, чем для группового.

Средние квадратические отклонения σ(d_г/d) мало зависят от d_i, численные значения СКО для рассмотренных пород и потоков колеблются в небольшом диапазоне.

Случайная величина d_г/d не противоречит нормальному закону (некоторые выборки с худшей сходимостью одновременно описаны и законом Эрланга). Проверка на гипотетические распределения величины d_г/d проведена для бревен из мелкой, средней и крупной групп по толщине.

Таким образом, статистическое описание гнили в круглых лесоматериалах k-й породы (k Є {Б,Ос,С,...}) и для технологического потока с Д- способом деления лесоматериалов (Д Є {Гр, И}) включает вероятность встречи бревен с этим пороком, т. е.

Р^к_г(д) = f (d_i), Р^к_гс(д) = f (d_i);

вероятность встречи бревна с гнилью с выходом на один торец

Р^к_го(д) = Р^к_г(д) — Р^к_гс(д);

функцию плотностей распределения случайной величины dг/d

f(d_г/d)^к_д = [1/σ^к_dг/d(д)] exp {-0,5 σ²_dг/d(д) [(dг/d)^к_д — (г/d)^к_д]²}

с параметрами

(г/d)^к_д = f(d_i) и σ_dг/d(д) = f(d_i).

Уравнения регрессий приведенных параметров, область их применения даны в табл. 12.

Протяженность гнили в круглых лесоматериалах для бревен со сквозной гнилью равна длине бревна l_г = l, а в бревнах с гнилью на одном торце принимается по имеющимся в литературе сведениям.

Для бревен комлевой вырезки, определяемых по выведенной выше зависимости _кв = f(d_i), протяженность напенной гнили имеет статистическую связь с толщиной гнили на комлевом торце:

_г = f(d_i), σ_ег= f (d _гi).

Уравнения этих зависимостей для различных пород приведены в разделе 4.8 источника [20] и других работах [21].

Для бревен из вершинной и серединной части хлыстов распределение длины стволовой гнили установить невозможно [22], для дальнейших расчетов принимается по равномерному закону

0, при l_г ≤ 0 и l_г > l

f (l_г) =

1 /l, при 0 < l_г ≤ l.

10. Встречаемость сортиментов ссучками ираспределение сучков [1].

Изучали встречаемости бревен с сучками Р_с, числа сучков на единицу длины бревна n_c1 и толщины сучков d_c.

Существуют и другие показатели, в частности, насыщенность бревен сучками [23, с. 85–88], распределение брёвен по размеру максимального сучка [24], расположение сучков на поверхности брёвен по отношению к максимальному сучку [25].

Доля бревен с сучками уменьшается с увеличением d_i, и существует статистическая связь Р_с = f(d_i). Адекватность полученных уравнений регрессий подтверждается сравнением фактических величин дисперсионного отношения с табличными (F_ф >F_0.05) для всех случаев, кроме осины для Гр-потока. Однако при рассмотрении зависимости для двух градаций сырья по толщине выявленная тенденция сохраняется и в последнем случае (при d_i до 25см Р_с = 0,22; при d_i ≥ 26см Р_с = 0,212).

Наибольшая встречаемость бревен с сучками наблюдается у осины, наименьшая — у березы. На индивидуальный поток по сравнению с групповым поступает сырье с большим содержанием бревен с сучками. Разница по Р_с для березы, осины и сосны, поступаемых на И-поток, на всех ступенях толщины сырья d_i несущественная, но имеются большие различия для каждой породы при сопоставлении технологических потоков. Результаты статистической обработки по Р_с приведены в виде регрессионных уравнений Р_с = f(d_i) — в табл. 13.

Число сучков на 1 м длины березовых и осиновых бревен n описывается логарифмически нормальным распределением, а для сосны — нормальным. Наибольшее число сучьев наблюдается у сосны — 4,34 шт./м, у березы и осины значения _с1 колеблются в зависимости от технологического потока в пределах 1,8–2,15 шт./м. Анализ значений _с1 и СКО σ_n для разных групп сырья по толщине позволяет в модели принять их не зависящими от ступеней толщины сырья. Принятые значения _с1 и σ_n приведены в табл. 13.

Средняя толщина сучка _с и стандарт σ_dc находятся в статистической зависимости от d_i (только у осины для Гр-потока значение F_ф < F_0.05). В индивидуальном технологическом потоке толщина сучьев и их вариация больше, чем у сырья для Гр-потока. Однако различие по d_с по породам в каждом типе потока не столь существенно. Эмпирические распределения сучков по толщине не противоречат логарифмически нормальному распределению. Проверка проводилась по Р(χ²) для результирующих выборок из мелкой, средней и крупной групп сырья по толщине. Близость распределений величины d_с логарифмически нормальному распределению на ступенях толщин сырья d_i оценена по соотношениям А/m_α>3 и Е/m_е>3.

В математической форме статистическое описание сучков в круглых лесоматериалах k-й породы для Д-технологического потока будет выглядеть следующим образом.

Таблица 13

Содержание бревен ссучками иих размерная характеристика

Поток	Порода	Регрессионные уравнения	Fф	F0.05	Коэф. ур-ний определены при di, см
И И И И	Б Б Б Б	Рс=0,0011d2i -0,0789di+1,4894 с1=2,03 шт/м; σn =1,25 шт/м с=-0,1479d2i+8,0016di -22,6888, мм σdc =-0,0463d2i+2,7782di -5,8248, мм	9,5 — 32,6 40,7	1,69 — 1,94 1,94	12–38 — 12–31 12–31
И И И И И	Ос Ос Ос Ос Ос	Рс=0,0013d2i -0,0898di +1,7336 с1=2,153 шт/м, σn=1,13 шт/м с =0,0081d2i +0,8600di +51,5043, мм с=70,5мм(di≤25см);dс=89,0мм(di≥26) σdc =-0,0680d2i +3,46di -10,0120, мм	18,5 — 1,9 — 2,4	1,66 — 1,98 — 1,98	12–40 — 12–32 — 12–32
И И И И	С С С С	Рс=0,0008d2i -0,0610di +1,2852 с1=4,34 шт/м; σn =1,87 шт/м с =0,0134d2i +0,7591di +28,0123, мм σdc =-0,0116d2i +0,9887di +3,2270, мм	9,2 — 15,9 4,0	1,66 — 1,98 1,98	12–40 — 12–31 12–31
Гр Гр Гр Гр	Б Б Б Б	Рс=0,0011d2i -0,0571di +0,7999 с1=1,80 шт/м; σn =0,90 шт/м с =-0,1013d2i +5,0187di -11,4997, мм σdc =-0,0125d2i +0,9450di +2,4875, мм	12,0 — 6,5 5,7	1,75 — 2,46 2,46	12–36 — 13–29 13–29
Гр Гр Гр Гр Гр Гр	Ос Ос Ос Ос Ос Ос	Рс=0,0004d2i -0,0234di di +0,5388 Рс=0,220(di <25см); Рс=0,212(di>26см) с1=2,25 шт/м; σn =0,95 шт/м с= -0,0228d2i+1,1937di di+35,7005, мм с =50,2мм(di≤25см);dс=51,8мм(di≥26) σdc = -0,0616d2i +2,2325di -15,0422, мм	1,0 — — 1,0 — 5,3	1,83 — — 2,50 — 2,50	12–36 — — 13–29 — 13–29

Встречаемость бревен с сучками:

Р^к_с(д) = f (d_i).

Распределение числа сучков на 1 м длины сосновых бревен:

f(n^с_с1(n)) = [1 /σ^c_n(n)] exp { — 0,5 [(n^с_с1(n)- ^с_с1(n))/σ^c_n(n]²}.

Распределение числа сучков на 1 м длины бревен лиственных пород:

f(n^к_с1(д)) = [1 /σn^к_с1(д)] exp { — 0,5 [(lnn^к_с1(д) — a) /σ]²}

с параметрами

a = ln^к_с1(д) — 0,5 ln{(σ^к_n(д) /^к_с1(д))² + 1}; σ²= 2 ln^к_с1(д)- 2a.

Распределение толщины сучков на круглых лесоматериалах:

f(d^к_с(д)) = [1 /σd^к_с1(д)] exp { — 0,5 [(lnd^к_с(д)- a)/σ]²}

с параметрами

a = ln^к_с1(д) — 0,5 ln{(σd ^к_c(д) /^к_с(д))² + 1}; σ²= 2 ln^к_с(д)- 2a.

^к_с(д) и σ^к_c(д) = f (d_i).

Численные значения параметров Р_с, ^к_с1(д), σ^к_n(д), ^к_с(д) и σ^к_c(д) находятся по уравнениям регрессий, приведенных в табл. 13.

11. Встречаемость сортиментов скривизной ираспределение кривизны [18, 1].

Существенная часть круглых лесоматериалов имеет кривизну. Кривизна К, как случайная величина, подчиняется вероятностному закону со средним значением и стандартом σ_к, характеризуется встречаемостью бревен с кривизной Р_к. На основании изучения охарактеризованы перечисленные характеристики для технологических потоков с учетом основного фактора — толщины сырья d_i.

Наибольший удельный вес бревен с кривизной наблюдается у березы (43 %), осина меньше подвержена этому сортообразующему пороку (20 %), а у сосны совсем небольшое число бревен с кривизной. С увеличением d_i значения Р_к у всех пород снижаются. Полученные статистические связи Р_к = f (d_i) для бревен березы, осины и сосны достоверны.

Эмпирические распределения кривизны К асимметричны и одинаково хорошо описываются как логарифмически нормальным законом, так и законом Эрланга. Статистики и σ_к зависят от породы и типа технологического потока, а с толщиной сырья d_i у них статистическая связь очень проблематична (критерий Фишера не подтверждает ее), что видно из анализа табл. 14. Для практического пользования принимается модель кривизны вида:

Встречаемость бревен с кривизной

Р = f(d_i).

Функция плотностей распределения К:

f(К^к_с(д)) = [1 /σК^к_(д)] exp { — 0,5 [(lnК^к_с(д)- a)/σ]²},

где a = ln^к_(д) — 0,5 ln{(σ^к_к(д) /^к_(д))+ 1}; σ²= 2 ln^к_{(д) —} 2а.

Таблица 14

Содержание бревен скривизной иее размерная характеристика

Поток	Порода	Регрессионные уравнения	Fф	F0.05	Коэф. ур-ний определены при di, см
Гр	Б	Рк=-0,0002d2i +0,0012di +0,5026	8,1	1,64	12–44
Гр	Б	=-0,0030d2i +0,1184di +2,4300, %	1,6	1,83	12–32
Гр	Б	=3,573 %(di ≤25); K=3,344 %(di ≥26)	-	-	-
Гр	Б	σк=-0,0021d2i +0,0524di +1,4174, %	3,5	1,83	12–32
И	Б	=0,0008d2i -0,0269di +5,2411, %	1,0	1,66	12–40
И	Б	=5,155 %(di ≤25);K=4,957 %(di ≥26)	-	-	-
И	Б	σк =-0,0024d2i +0,1079di +1,2903, %	1,2	1,66	12–40
И	Б	σк =2,517 %(di ≤25); σк =2,246 %(di ≥26)	-	-	-
Гр	Ос	Рк=-0,00008d2i -0,0115di +0,5066	9,7	1,79	12–34
Гр	Ос	=-0,0063d2i +0,2306di +1,0737, %	52,5	2,20	14–26
Гр	Ос	σк =-0,0082d2i +0,2787di -0,9998, %	1,1	2,20	14–26
Гр	Ос	σк =1,317 %(di ≤25); σк =0,606 %(di ≥26)	-	-	-
И	Ос	=-0,0026d2i +0,0573di +4,1278, %	1,4	1,90	12–30
И	Ос	=4,343 %(di ≤25);K=3,458 %(di ≥26)	-	-	-
И	Ос	σк =-0,0023d2i +0,0512di +2,2025, %	1,2	1,90	12–30
И	Ос	σк =2,387 %(di ≤25); σк =1,870 %(di ≥26)	-	-	-
И	С	Рк=-0,0002d2i +0,0013di +0,0978	2,3	2,01	12–36
И	С	=3,500 %(di ≤25); K=3,545 %(di ≥26)	-	-	-
И	С	σк =2,388 %(di ≤25); σк =2,362(di ≥26)	-	-	-

12. Выводы. Практическая реализация.

Материалы, приведённые в данной работе, показывают, что размерные и качественные параметры сортиментов являются случайными величинами. Это относится в первую очередь к диаметру, сбегу, длине, породе, сучкам, гнили и кривизне.

Диаметр d у сортиментов описывается теоретическим вероятностным законом, тип которого зависит от среднего диаметра. Величины средних квадратических отклонений случайной величины d находятся в функциональной зависимости от среднего значения d. Основным фактором, влияющим на статистические параметры величины d у сортиментов, является средний объём хлыста. Средний диаметр сортимента является также случайной величиной, среднее значение которой равняется генеральной средней величине d. Для решения некоторых частных задач получены значения среднего диаметра для пород и места вырезки из хлыста.

Длину у сортиментов можно описать нормальным распределением. Распределения длины могут быть и полимодальными.

Сбег у сортиментов описывается нормальным распределением. Параметры распределения зависят от вида сортимента, его диаметра и длины, породы, бонитета.

Породный состав сортиментов не постоянен во времени и его колебания можно принять по нормальному закону.

Параметры статистической модели сортообразующих пороков (сучки, гниль, кривизна) у сортиментов также зависят от природно-климатических и производственных условий.

Представленное математическое описание размерно-качественных параметров круглых лесоматериалов послужило основой для имитационного моделирования параметров сырья и выхода из него готовой продукции [26]. Имитационное моделирование проводилось на компонент-программах СЫРЬЁ и ПРОДУКЦИЯ, входящих в комплекс-программу ЦЕХ [27, 28]. Изучено влияние размерных параметров сырья на работу лесообрабатывающего станка [29], на сортовой состав круглых лесоматериалов [30] и выход пилопродуции [31, 28].

Литература:

1. Чамеев В. В. Совершенствование технологических процессов лесопильно-тарных цехов лесозаготовительных предприятий: дисс. на соиск. ученой степени канд. техн. наук / Чамеев Василий Владимирович. — М.: МЛТИ, 1991. – 261 с.
2. Редькин А. К. Основы моделирования и оптимизации процессов лесозаготовок: учебник для вузов / А.К Редькин. – М.: Лесн. пром-сть, 1988. – 256 с.
3. Редькин А. К. Выбор лесоскладских машин и технологии в зависимости от раз-мерно-качественных характеристик обрабатываемого сырья: Учебное пособие по курсу «Технология и машины лесоскладских работ» / А. К. Редькин, А. Я. Чувелёв. – М.: МЛТИ, 1981. – 76 с.
4. Воевода Д. К. Выбор лесообрабатывающих машин в зависимости от размерных характеристик круглых лесоматериалов / Д. К. Воевода, А. К. Редькин, Г. А. Рахманин, А. Я. Чувелёв. – Обзор. информ. – ВНИПИЭИлеспром, 1975. – 33 с. (Лесоэксплуатация).
5. Чувелев, А. Я. Зависимость толщины круглых лесоматериалов от объема хлыста / А. Я. Чувелёв // Науч. тр. /ЦНИИМЭ — 1974. – Комплексная механизация работ на нижнем складе. – Сб. № 139 — C. 16–21.
6. Чамеев В. В. Математическая модель размерно-качественных параметров круглых лесоматериалов / В. В. Чамеев // Вклад молодых ученых и специалистов в осуществление комплексной механизации и автоматизации лесосечных и нижнескладских работ: Тез. докл., Свердловск: УЛТИ. – 1987. – С. 51–52.
7. Пижурин А. А. Основы моделирования и оптимизации процессов деревообработки: учебник для вузов / А. А. Пижурин, М. С. Розенблит — М.: Лесн. пром-сть, 1988. – 296 с.
8. Туровский Т. А. Автоматизация в шпалопилении / Т. А. Туровский, И. М. Грамотеев. — М.: Лесн. пром-сть, 1973. – 152 с.
9. Волынский С. Н. Распределение по длинам круглых лесоматериалов, поставляемых в вагонах / С. Н. Волынский // Лесоэксплуатация и лесосплав: Науч.-техн. реф. сб. / ВНИПИЭИлеспром. – 1987. — № 6. — С. 10.
10. Заливко Б. М. Расход низкокачественной древесины при выработке пилопродукции / Б. М. Заливко, У. Э. Яунсилс, Л. П. Тютикова. — Обзор. информ. – М.: ВНИПИЭИлеспром, 1974. – 47 с.
11. Аксенов П. П. Теоретические основы раскроя пиловочного сырья / П. П. Аксёнов. – М.-Л.: Гослесбумиздат, 1960. – 216 с.
12. Тюкина Ю. П. Технология лесопильно-деревообрабатывающего производства: учебник для техникумов / Ю. П. Тюкина, С. Н. Рыкунин, В. С. Шалаев. – М.: Лесн. пром-сть, 1986. – 280с.
13. Соболев И. В. Оптимизация раскроя пиловочного сырья / И. В. Соболев. — М.: Лесн. пром-сть, 1971. – 38 с. (НТО лесной промышленности и лесного хозяйства. Общественный заочный институт. Из цикла заочных лекций).
14. Кочегаров В. Г. Технология и машины лесосечных и лесовосстановительных работ / В. Г. Кочегаров, Л. Г. Федяев, И. А. Лавров. – М.: Лесн. пром-сть, 1970. – 400 с.
15. Ветшева В. Ф. Раскрой крупномерных бревен на пиломатериалы / В. Ф. Ветшева. – М.: Лесн. пром-сть, 1976. – 168 с.
16. Прокофьев Г. Ф. Интенсификация пиления древесины рамными и ленточными пилами / Г. Ф. Прокофьев. – М.: Лесн. пром-сть, 1990. – 240 с.
17. Окунев Г. С. Изготовление железнодорожных шпал и переводных брусьев: техническое и методическое пособие / Г. С. Окунев, А. Г. Шевелёв. — М.: Лесн. пром-сть, 1967. – 168 с.
18. Обвинцев В. В. Математическое описание основных параметров низкокачественного древесного сырья / Н. В. Лившиц, В. В. Обвинцев, В. В. Чамеев // Межвуз. сб. науч. тр. / Ленингр. лесотех. акад. – 1979. – Вып. 8. – Лесосечные, лесоскладские работы и сухопутный транспорт леса. – С. 125–127.
19. Стеймацкий Р. М. Справочник по шпалопилению и лесопилению / Р. М. Стеймацкий, Ф. И. Красиков. – М.: Лесн. пром-сть, 1971. – 286 с.
20. Чамеев В. В. Природно-производственные условия лесного фонда и размерно-качественная характеристика деревьев и хлыстов: учеб. пособие / В. В. Чамеев, Б. Е. Меньшиков, В. В. Обвинцев. – Екатеринбург: Урал. гос. лесотехн. ун-т, 2001. – 108 с. (Сер. Основы проектирования лесопромышленных производств. Системный подход).
21. Меньшикова А. И. Разработка безотходной технологии раскряжевки хвойных хлыстов в условиях береговых складов с молевым лесосплавом: автореф. дис. на соиск. ученой степени канд. техн. наук / Меньшикова Августа Ильинична. – Л.: Ленингр. лесотех. акад., 1984. – 20 с.
22. Степаков Г. А. Оптимизация производства круглых лесоматериалов / Г. А. Степаков. – М.: Лесн. пром-сть, 1974. – 160 с.
23. Кислый В. В. Оценка качества продукции лесной и деревообрабатывающей промышленности / В. В. Кислый. — М.: Лесн. пром-сть, 1975. – 224 с.
24. Захарьин Г. И. Распределение хвойных круглых лесоматериалов по размеру основного порока / Г. И. Захарьин // Механическая обработка древесины // Науч.-техн. реф. сб. / ВНИПИЭИлеспром. – 1979. – С. 11–12.
25. Захарьин Г. И. Распределение сучков как фактор оптимизации плана раскроя соснового пиловочного сырья / Г. И. Захарьин, С. И. Малыгин // Механическая обработка древесины // Науч.-техн. реф. сб. / ВНИПИЭИлеспром. – 1975. – С. 11.
26. Чамеев В. В. Имитационное моделирование размерно-качественных параметров круглых лесоматериалов и выхода пилопродукции в лесообрабатывающих цехах лесопромышленных предприятий / В. В. Чамеев, А. Н. Кривоногова // Леса России и хозяйство в них: жур. Вып. 1(31) / Урал. гос. лесотехн. ун-т.- Екатеринбург, 2009. — С. 69–73.
27. Чамеев В. В. Алгоритмы и машинные программы для исследования технологических процессов лесообрабатывающих цехов: архитектура комплекс программы «ЦЕХ» / В. В. Чамеев, С. Б. Якимович, Ю. В. Ефимов, Г. Л. Васильев // Молодой ученый. – 2015. – № 10 (90). – Часть III. – С. 357–360.
28. Чамеев В. В. Математическая модель и алгоритм по определению сортового состава круглых лесоматериалов и выхода готовой продукции / В. В. Чамеев, Г. Л. Васильев // Вестник МГУЛ-Лесной вестник, 2014. – № 2. – С. 156–162.
29. Чамеев В. В. Влияние параметров сырья на временные показатели работы станков при раскрое круглых лесоматериалов / В. В. Чамеев, В. В. Иванов // Урал промышленный – Урал полярный: социально-экономические и экологические проблемы лесного комплекса: Сборник материалов международной научно-технической конференции. – Екатеринбург: УГЛТУ, 2007. – С. 244–247.
30. Чамеев В. В. Влияние размерных параметров сырья на сортовой состав круглых лесоматериалов / А. А. Еремеев, В. В. Чамеев // Научное творчество молодёжи — лесному комплексу России: матер. VI Всерос. науч.-техн. конф. / Урал. гос. лесотехн. ун-т. – Екатеринбург, 2010. – Ч.1. – С. 280–282.
31. Чамеев В. В. Сортовой состав круглых лесоматериалов и выход пиломатериалов и заготовок общего назначения / В. В. Чамеев, Е. В. Гаева, П. Е. Харисов // Деревообработка: технологии, оборудование, менеджмент XXI века: Труды международного евразийского симпозиума. — Екатеринбург: УГЛТУ, 2006. – С. 23–27.