Проведена оценка преобразования Фурье на примере цифровой обработки сигналов, построены графики и смеси сигнала с шумом, исследован спектр сигнала.
Ключевые слова: дискретное Преобразование Фурье, спектр сигнала, белый шум, импульс.
Преобразование Фурье стало мощным инструментом, применяемым в различных научных областях. В некоторых случаях его можно использовать как средство решения сложных уравнений, описывающих динамические процессы, которые возникают под воздействием электрической, тепловой или световой энергии. В других случаях оно позволяет выделять регулярные составляющие в сложном колебательном сигнале, благодаря чему можно правильно интерпретировать экспериментальные наблюдения в астрономии, медицине и химии.
Быстрое преобразование Фурье (БПФ, FFT) — алгоритм быстрого вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем ![]() , требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющий сложность
, требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющий сложность ![]() . [1]
. [1]
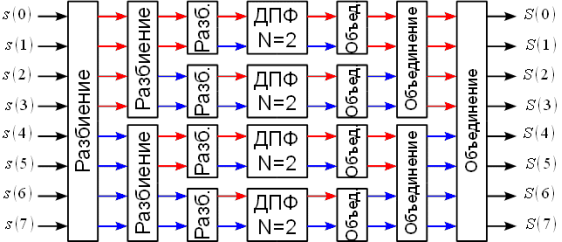
Рис. 1 Схема БПФ по основанию 2 с прореживанием по времени
Основой алгоритма, как видно по рис. 1, является «ДПФ N=2», именуемое операцией «Бабочка» [2], формула которой имеет следующий вид:
![]() (1)
(1)
где ![]()
Операция проста в реализации, но именно она определяет скорость работы алгоритма БПФ.
Алгоритм БПФ имеется во всех современных программных средах для решения технических задач. Например, в пакете прикладных программ MATLAB имеется готовая функция FFT. Её мы и будем использовать в данной работе.
Для того, чтобы оценить влияние широкополосного шума на спектр сигнала, используем следующий код в MATLAB:
|
clear all% Очистка памяти Tm=5;% Длина сигнала (с) Fd=512;% Частота дискретизации (Гц) A1=1;% Амплитуда первой синусоиды F1=13;% Частота первой синусоиды (Гц) An=3*A1;% Дисперсия шума (Попугаев) FftL=1024;% Количество линий Фурье спектра T=0:1/Fd:Tm;% Массив отсчетов времени Noise=An*randn(1,length(T));% Массившума Signal=A1*sind((F1*360).*T);% Массивсигнала FftS=abs(fft(Signal,FftL));% АмплитудыпреобразованияФурье FftS=2*FftS./FftL;% Нормировка спектра по амплитуде FftS(1)=FftS(1)/2;% Нормировка постоянной составляющей FftSh=abs(fft(Signal+Noise,FftL));%FFT для смеси сигнал+шум FftSh=2*FftSh./FftL;% Нормировка спектра по амплитуде FftSh(1)=FftSh(1)/2;% Нормировка постоянной составляющей subplot(2,1,1);% Выбор области окна для построения plot(T,Signal);% Построение сигнала title('Сигнал');% Подпись графика xlabel('Время (с)');% Подпись оси х графика ylabel('Амплитуда');% Подпись оси у графика subplot(2,1,2);% Выбор области окна для построения plot(T,Signal+Noise);% Построение смеси сигнал+шум title('Сигнал+шум');% Подпись графика xlabel('Время (с)');% Подпись оси х графика ylabel('Амплитуда');% Подпись оси у графика F=0:Fd/FftL:Fd/2-1/FftL;% Массив частот figure% Создаем новое окно subplot(2,1,1);% Выбор области окна для построения plot(F,FftS(1:length(F)));% Построение спектра Фурье сигнала title('Спектр сигнала');% Подпись графика xlabel('Частота (Гц)');% Подпись оси х графика ylabel('Амплитуда');% Подпись оси у графика subplot(2,1,2);% Выбор области окна для построения plot(F,FftSh(1:length(F)));% Спектр сигнала+шума title('Спектр сигнала');% Подпись графика xlabel('Частота (Гц)');% Подпись оси х графика ylabel('Амплитуда');% Подпись оси у графика |
В результате получаем следующие графики:
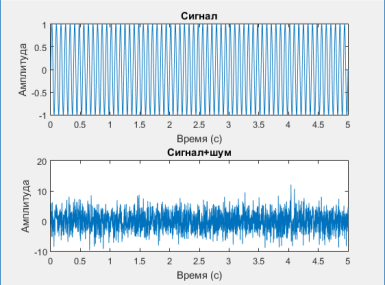
Рис. 2. График сигнала (наверху) и смеси сигнала и шума (внизу)
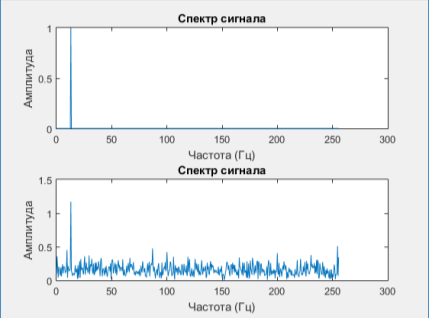
Рис. 3. Спектр сигнала (наверху) и спектр смеси сигнала и шума (внизу)
Из полученных графиков видно, что несмотря на то, что полезного сигнала не видно на фоне шума, спектральная характеристика позволяет определить его частоту и амплитуду. Таким образом, преобразование Фурье устойчиво к белому шуму и позволяет выделить полезный сигнал на фоне весьма значительной помехи.
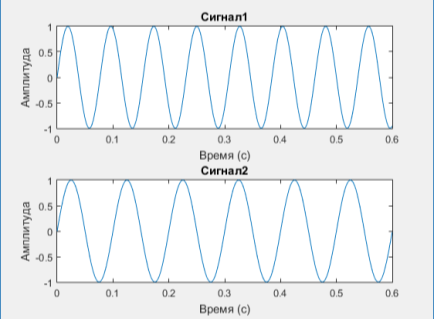
Рис. 4. Сигнал с неполным числом периодов (наверху) и полным (внизу)
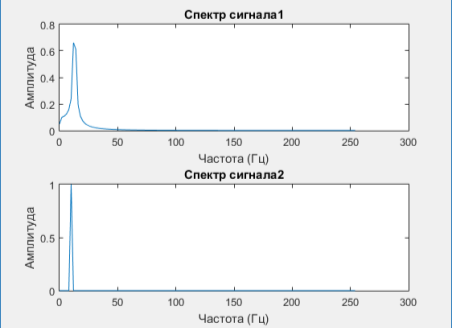
Рис. 5. Спектры сигналов с рис. 4
Мы наблюдаем заметное расширение для 1-го сигнала (с неполным числом периодов). Причина этого в том, что мы задаем сигнал, ограниченный во времени, а для преобразования Фурье этот сигнал «продолжается» и считается непрерывным. Проиллюстрировать это следует так, как показано на рис. 6

Рис. 6
Скачок, выделенный на рисунке 6 и дает расширение спектра. Следует отметить, что этот скачок не приводит к появлению высокочастотной составляющей спектра, а напоминает по форме спектр импульса.
Таким образом можно сделать вывод о том, что при одинаковой частоте, но разном количестве временных отсчетов, мы получим аналогичное искажение спектра сигнала.
Литература:
- Ряды Фурье. Интегралы Фурье. Преобразование Фурье: учебно-методическое пособие / сост.: Н. П. Семенчук, Н. Н. Сендер; Брест. Гос. Ун-т имени А. С. Пушкина. — Брест: БрГУ, 2011. — 42 с.
- Колмогоров А. Н., С. В. Фомин. Элементы теории функций и функционального анализа. М.: Наука, 1981, 544 с.
- Scientific American, Издание на русском языке, № 8 Август 1989 с. 48–56.







