В современном мире важным вопросом выступает эффективное, безболезненное лечение. Самым главным является вылечить пациента как можно быстрее. Поэтому создан наноробот, который способен доставлять лекарство прямо к источнику заболевания.
Ключевые слова: наноробот, манипулятор, динамическая система, биосовместимость.
In today's world an important issue appears effective, painless treatment. The most important thing is to cure the patient as quickly as possible. Therefore nanorobot created, which is capable of delivering the drug directly to the source of the disease.
Keywords: nano robot manipulator, dynamic system, biocompatibility.
На сегодняшний день роботы стали очень важным элементов в жизни людей, особенно в медицине. Создание медицинских нанороботов –важное направление в робототехнике. Успехи в этой области были достигнуты сравнительно недавно.
Рассмотрим медицинский наноробот, размером с шарик от авторучки (рис.1.), который способен перемещаться во всех направлениях. Робот способен передвигаться не только по крупным артериям, но и по узким кровеносным сосудам. Это позволяет проводить сложные виды лечения без хирургического вмешательства. Наноробот будет вводиться иглой в определенную часть тела. Робот полезен при лечении онкологических заболеваний, доставляет лекарство прямо к злокачественному образованию.
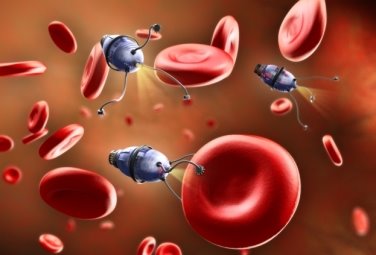
Рис.1. Наноробот
Робот изготавливается из алмазоида или сапфироида. Это обеспечивает биосовместимость человека и наномашины. Оборудованием робота являются телескопические захваты и жгутики, которые могут складываться в корпус робота для лучшего передвижения в кровеносном русле.
В нашем случае используется метод декомпозиции динамических систем антропоморфных манипуляторов с помощью статической обратной связи по состоянию системы. Этот метод хорошо себя проявляет в применении к манипуляционным роботам с жесткими соединениями.
Можно осуществить декомпозицию динамической системы манипулятора с помощью эластичных соединений, или воспользоваться методом согласования нелинейных моделей. Построение на основании этого метода управления, решающее задачу декомпозиции, является динамической обратной связью по состоянию системы.
Манипулятор можно рассматривать как структуру последовательно соединенных между собой твердых тел (звеньев) и сочленений между ними. Если передаточные механизмы, связывающие двигатели со звеньями, обладают упругостью, то модель робота включает в себя несколько твердых тел, из которых некоторые могут быть управляемы. Движение такой модели может быть описано системой уравнений второго порядка
q࣫̈ = B (q)-1 [m(t)-e(q)-c(q,q̇)], (1)
где q-вектор обобщенных координат, B(q)-матрица инерционности размера, c(q,q̇)- центробежные и кориолисовы силы, m(t) — вектор обобщенных управляющих сил, у которого четные элементы равны нулю.
В случае эластичных сочленений вектор f(x) и матрица g(x) имеют вид
f(x)=![]()
g(x)=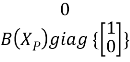 (2)
(2)
Выход в системе для рассматриваемой модели манипулятора может быть определен как вектор перемещений звеньев. Входной сигнал состоит из нулевых элементов вектора.
Для эластичных роботов решить задачу декомпозиции можно с помощью управления, использующую динамическую обратную связь которая определяется равенствами
ᶓ̇= a (x, ᶓ)+b(x,ᶓ)v
u=c(x,ᶓ)+d(x,ᶓ)v (3)
где ᶓ-компонентный вектор состояний, v- компонентный вектор, представляющий собой вектор нового входной сигнала.
Построение искомого динамического управления проводится по образцу, приведенному в доказательстве теоремы с учетом особенностей рассматриваемой системы манипулятора. Результирующая системы управления представляет собой динамическую систему в форме с входными сигналами v1,v2, выходными сигналами u1,u2 и четырехкомпонентным вектором состояния ᶓ=(ᶓ1ᶓ2ᶓ3ᶓ4). Она имеет вид
ᶓ̇1=ᶓ2
ᶓ̇2=ᶓ3
ᶓ̇=ᶓ4
ᶓ̇4=v1
u1=α̅̅1 (x,ᶓ)+β̅11(x)v̇1+β̅12v2 (4)
u2=-f6 (x)/g62(x)+1/g62(x)*ᶓ1
где α̅1=-DA2(Lf-6h2), β̅11=-D (A3cosx4+A2), β̅12=DA2
D=N1N2JRZ1JRZ2/K1,K2, Lfh2=(ðh2/ðx1…ðh2/ðx8)f̅,Lfkh2=Lf-(Lf-k-1h2).
Использование динамического управления позволяет осуществить декомпозицию рассматриваемой системы манипулятора и так организовать поведение этой системы, чтобы оно совпадало с поведением линейной управляемой системы.
Литература:
- Поезжаева Е. В. Промышленные роботы: учебное пособие в 3 ч. — М.; УМО АМ МВТУ им. Баумана; изд-во ПГТУ, 2009.
- http://bonifazi2010.narod.ru/







