Реализация алгоритма шифрования RSA на языке программирования LabView

 

Статья посвящена реализации алгоритма шифрования на открытом ключе RSA.

LabVIEW (англ. Laboratory Virtual Instrumentation Engineering Workbench) — это среда разработки и платформа для выполнения программ, созданных на графическом языке программирования «G» фирмы National Instruments (США) [1]. LabVIEW позволяет реализовать алгоритмы ООП, а так же содержит визуальную часть, подходящую для реализации алгоритмов, связанных с передачей зашифрованных данных, в частности методом RSA.

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других [2].

RSA алгоритм, относящийся к шифрованию на открытом ключе, соответственно его реализация должна состоят из принимающего лица B(Bob), являющегося инициатором обмена данными и отправляющего лица A (Alice), имеющего доступ к открытому хранилищу ключей.

Алгоритм RSA:

1.                Выбираются два различных случайных простых числа p и q.
2.                Вычисляется их произведение 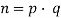, которое называется модулем.
3.                Вычисляется значение функции Эйлера от числа n:

.

4.                Выбирается целое число e (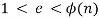), взаимно простое со значением функции .

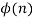Число e называется открытой экспонентой (англ. public exponent)

5.                Вычисляется число d, мультипликативно обратное к числу e по модулю 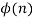, то есть число, удовлетворяющее сравнению:

.

Число d называется секретной экспонентой.

6.                Пара 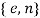публикуется в качестве открытого ключа RSA (англ. RSA public key).
7.                Пара 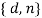играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.

Описание алгоритма. На языке программирования LabVIEW алгоритм RSA должен быть реализован как минимум из трех блоков:

1.                Блок отправляющего лица A (Alice)
2.                Блок принимающего лица B (Bob)
3.                Блок, выступающий в роли хранилища пары открытых ключей, реализованный в виде глобальной переменной (PublicKeyStorage)

Так же программа должна содержать вспомогательные блоки для реализации генератора простых чисел, а также реализации алгоритма Евклида и вычисления односторонней функции с секретной дверью (Trapdoor One-Way Function).

Инициатором передачи данных выступает абонент В, соответственно он должен сгенерировать открытую и закрытую пары ключей и положить их в открытое хранилище. После этого абонент А должен забрать пару открытых ключей и зашифровать на них текстовый файл, который может по небезопасному каналу данных передать абоненту В, после чего последний, зная пару закрытых ключей, сможет расшифровать сообщение в исходный текстовый файл.

Описание программы. Программа состоит из блоков, описанных в разделе «Описание алгоритма». Существует необходимость разобрать их подробнее, следуя шагам алгоритма шифрования RSA, также описанном выше.

Генерация пары чисел. На данном этапе происходит генерирование двух простых случайных чисел, при помощи ГПСЧ (Генератор ПсевдоСлучайных Чисел), встроенного в LabView. Данный процесс происходит в два этапа.

Сначала в блоке Generate random number (Рис 1) происходит набор произвольного числа заданной длины, по умолчанию трехразрядного.

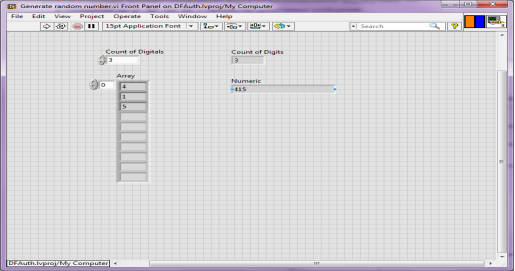
Рис. 1. Блок Generaterandomnumber

 

Формирование числа происходит из случайно сгенерированных цифр от нуля до девяти, с дальнейшим преобразованием из массива в число. В текущих версиях RSA используются цифры с сотнями разрядов. Технически данная возможность реализована. Возможные неполадки можно исправить увеличив тип Int32 до типа Int64 или более.

Далее в блоке Generate Prime Number происходит преобразование случайного числа в простое. Для увеличения криптостойкости происходит складывание случайного числа с еще одним случайным числом такой же длины, после чего перебором в цикле с помощью модуля RT Mathscript подбирается простое число, основанное на данном случайном.

Таким образом, можно сгенерировать два простых числа, заданной длины.

Генерация пар ключей. Генерация ключей происходит в блоке Generate Keys (Рис. 2) из двух простых чисел, сгенерированных на предыдущем этапе.

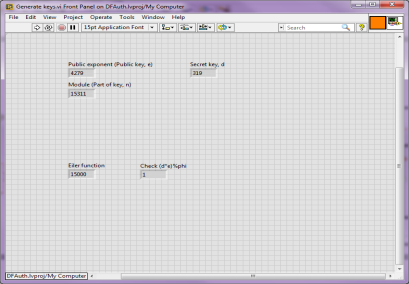
Рис. 2. Блок Generate Keys

 

В первом кадре структуры «Sequence» вычисляется модуль и функция Эйлера, путем перемножения двух простых чисел. На втором кадре вычисляются все возможные значения открытой экспоненты, и случайно выбирается одно из значений. Сами значения заносятся в массив.

Непосредственное добавление элементов случается после прохождения числа итераций сложенного с двойкой через расширенный алгоритм Евклида, чтобы найти наибольший общий делитель, так как открытая экспонента должна быть взаимно простым с функцией Эйлера. Структура расширенного алгоритма Евклида реализована в блоке Euclide Algorithm.

Алгоритм Евклида — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел. Алгоритм назван в честь греческого математика Евклида, который впервые описал его в VII и X книгах «Начал» [3].

Таким образом мы можем вычислить секретную экспоненту и модуль, играющие роль открытого ключа. Так же при помощи алгоритма Евклида вычисляется и закрытый ключ.

 Инициализация обмена данными. За инициализацию обмена отвечает абонент В. Его интерфейс реализован в блоке Bob (Рис. 3). По нажатию на кнопку «Generate» запускается цепочка, генерирующая пары ключей и заносящая их в блок Public Key Storage.vi.

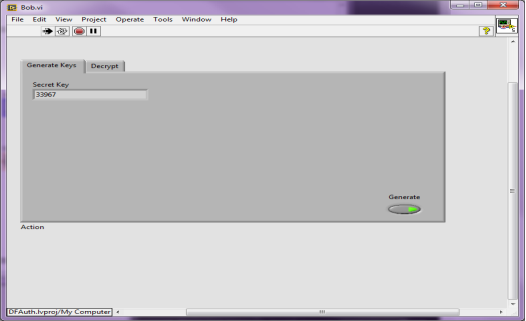
Рис. 3. Блок Bob инициализация

 

 Зашифрование. После генерации ключей абонент А может взять открытую пару ключей и зашифровать текстовый файл, для передачи по ненадежному каналу связи. Интерфейс А реализован в блоке Alice (Рис 4).

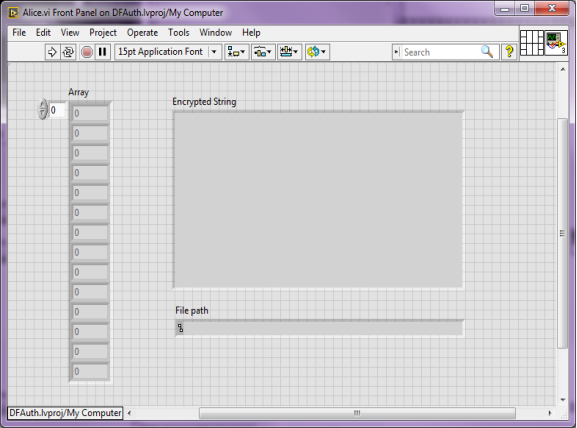
Рис. 4. Блок Alice

 

После диалогововго выбора файла происходит его шифрорвание с помощью односторонней функции , реализованной в блоке One-Way Function (Рис. 5)

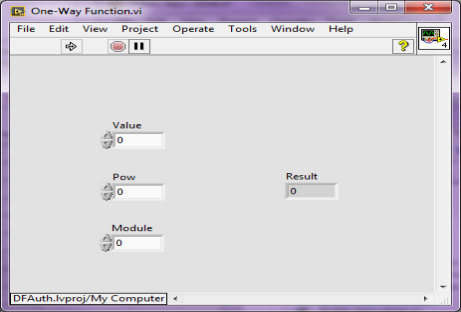
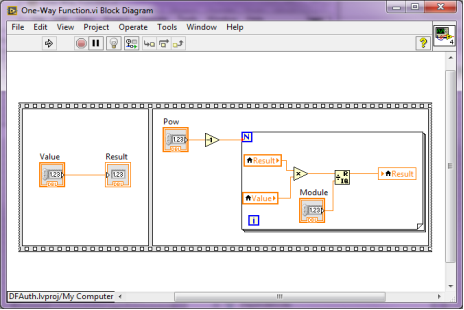
Рис. 5. Блок One-Way Function.vi

 

После этого абонент Б может получить зашифрованное сообщение. Пример работы алгоритма шифрования на ключе 33967 представлен на Рис. 6.

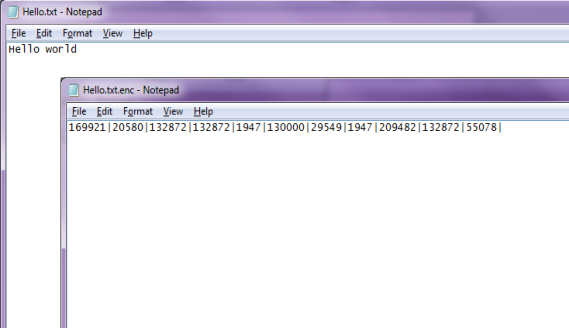
Рис. 6. Пример зашифрованного сообщения

 

 Расшифровка сообщения. После получения сообщения у абонента В становится доступен режим расшифровки, как графический, так и алгоритмический, представленный на Рис. 7.

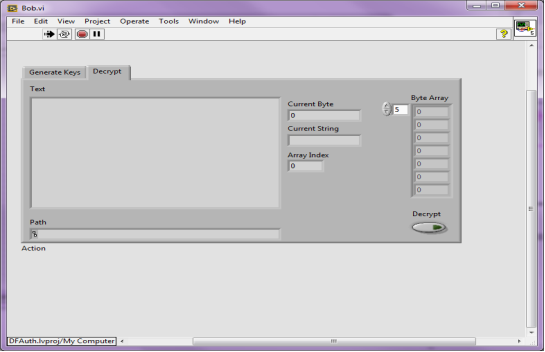
Рис. 7. Блок Bob расшифровка

 

Через одностороннюю функцию также можно расшифровать сообщение, зная секретный ключ. На этом работа алгоритма считается оконченной.

 Заключение. В статье реализовывался алгоритм криптографического шифрования RSA. На графическом языке программирования LabVIEW конечный код проще понимать и поддерживать. Так же содержатся мощные инструменты для построения графического интерфейса, которые позволяют реализовывать пользовательскую часть программы.

Главным минусом является занимаемое время на построение алгоритмов, что не мешает писать качественный и в прямом смысле слова красивый код, а также данный метод может найти широкое распространение в сфере обучения криптобезопасности в силу наглядности используемых алгоритмов.

 

Литература:

 

1.                Русский официальный сайт LabVIEW [Электронный ресурс] — Режим доступа: http://www.labview.ru/
2.                Martin Gardner. Mathematical Games: A new kind of cipher that would take millions of years to break (англ.) // Scientific American. — 1977.
3.                Щетников А. И. Алгоритм Евклида и непрерывные дроби. — Новосибирск: АНТ, 2003.