Криптографическая система RSA с открытым ключом, предложенная в работе [2, с. 120] получила широкое распространение в настоящее время. Эта системаподдерживает большинство электронных коммерческих коммуникаций. Данная система получила свое название — сокращение, составленное из первых букв фамилий её авторов: Rivest R., Shamir A., Adleman L.
Так как дискретное логарифмирование и факторизация целых чисел [4, с. 21] являются сложными вычислительными задачами теории чисел, то данная система является безопасной (при правильном использовании, учитывая критические работы по изучению её свойств).
Обозначения
![]() множество целых чисел;
множество целых чисел;
![]() — квантор принадлежности;
— квантор принадлежности;
![]() — Функция Эйлера от натурального числа
— Функция Эйлера от натурального числа ![]() ;
;
![]() наибольший общий делитель целых чисел
наибольший общий делитель целых чисел ![]() ;
;
![]() — целое число
— целое число ![]() делит нацело целое число
делит нацело целое число ![]() .
.
Диофантовы уравнения — уравнения, в которых неизвестные величины выражаются целыми числами (по имени древнегреческого ученого Диофанта, жившего в III в. н. э. До нас дошли шесть его работ, фундаментального труда «Арифметика», где рассматриваются разнообразные уравнения с целыми и рациональными неизвестными и обсуждаются способы решения таких уравнений)
Функция Эйлера — есть количество ![]() , удовлетворяющих условиям
, удовлетворяющих условиям ![]() [6, c. 70]
[6, c. 70]
Два целых числа
Первообразный корень — целое число g, являющееся взаимно простым с модулем m, если показатель его степени равен ![]()
![]()
Алгоритм системы RSA
Два лица (пусть будут) A и B хотели бы выработать общий тайный ключ для последующего шифрования информации.
Данные:
Простое число p, первообразный корень g по модулю p, секретный ключ ![]() абонента A, секретный ключ
абонента A, секретный ключ ![]() абонента B.
абонента B.
Поиск:
Общий ключ ![]() ,
, ![]() , известный только абонентам A и B.
, известный только абонентам A и B.
Действия:
-
Абоненту A вычислить
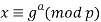 и отправить результат абоненту B.
и отправить результат абоненту B.
-
Абоненту B вычислить
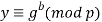 и отправить результат абоненту A.
и отправить результат абоненту A.
-
Абоненту A вычислить
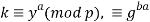
-
Абоненту B вычислить
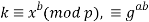
Схема шифрования RSA
Абонент B генерирует два больших простых числа p и q и вычисляет произведение
Пара чисел ![]() объявляется открытым ключом абонентом B, при этом скрывается секретная информация —
объявляется открытым ключом абонентом B, при этом скрывается секретная информация — ![]() и
и ![]() .
.
Секретный ключ: число ![]() .
.
Заметим, что для расшифрования достаточно знать пару чисел ![]() .
.
Алгоритм шифрования
– Сообщение ![]()
– A вычисляет, взяв данные открытого ключа абонента B ![]() :
:
![]()
– и отправляет результат B
– Абонент B, получив данное сообщение, вычисляет:
![]()
Корректность алгоритма: согласно теореме Ферма [6, с. 90], для каждого целого числа
(![]() )
) ![]()
Операции шифрования и расшифрования являются быстро выполнимыми.
Главным вопросом для исследования криптосистемы RSA является выбор параметров ![]() и
и ![]() , таких что решение задачи сравнения:
, таких что решение задачи сравнения:
![]()
является сложным относительно любых параметров скрытного ключа, или нахождения самого ![]() .
.
Замечание: пусть среди открытых ключей найдётся пара удовлетворяющая условию ![]() , взаимно простые натуральные ключи (не произведение двух простых чисел), тогда чтение сообщения
, взаимно простые натуральные ключи (не произведение двух простых чисел), тогда чтение сообщения ![]() , зашифрованного данными ключами, можно осуществить бесключевым способом:
, зашифрованного данными ключами, можно осуществить бесключевым способом:
![]()
![]()
Тогда существуют ![]() , такие что выполнено сравнение:
, такие что выполнено сравнение:
![]() ,
,
так как
![]()
Атака с помощью квантового компьютера
С помощью квантового компьютера, если он будет построен, можно будет взломать RSA, так как квантовый алгоритм Шора [3, c. 124] позволяет осуществить факторизацию больших чисел за достаточно короткое время. Разложив модуль ![]() на простые множители (это можно сделать за время
на простые множители (это можно сделать за время ![]() используя
используя ![]() логических Q-битов), можно будет вычислить секретный показатель
логических Q-битов), можно будет вычислить секретный показатель ![]() .
.
Применения: Электронная цифровая подпись
Пример: Подтверждение авторства. Пусть A хочет получить сообщение ![]() с подтверждением авторства от B
с подтверждением авторства от B
Вычисления BВычисления A
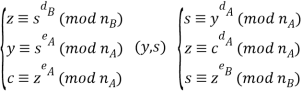
Если у A выполняется последнее сравнение, то он может считать, что сообщение отправлено именно абонентом B (подробнее [4, с. 38]).
Последние рекорды факторизации
RSA-220 (220 десятичных цифр). Факторизовано в мае 2016.
RSA-220 = 2260138526203405784941654048610197513508038915719776718321197768109445641817966676608593121306582577250631562886676970448070001811149711863002112487928199487482066070131066586646083327982803560379205391980139946496955261
RSA-220 = 68636564122675662743823714992884378001308422399791648446212449933215410614414642667938213644208420192054999687×32929074394863498120493015492129352919164551965362339524626860511692903493094652463337824866390738191765712603
RSA-768 (232 десятичных цифры). Декабрь 2009.
RSA-768 = 1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413
RSA-768 = 33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489×36746043666799590428244633799627952632279158164343087642676032283815739666511279233373417143396810270092798736308917
RSA-1024 (309 десятичных знаков) имеет 1024 бита, и пока что не факторизовано. За факторизацию был объявлен денежный приз в 100000 долларов США.
RSA-1024 = 135066410865995223349603216278805969938881475605667027524485143851526510604859533833940287150571909441798207282164471551373680419703964191743046496589274256239341020864383202110372958725762358509643110564073501508187510676594629205563685529475213500852879416377328533906109750544334999811150056977236890927563
RSA-2048 (617 десятичных знаков) имеет 2048 битов, и пока что не факторизовано. Это наибольшее из RSA-чисел и за него положен приз в 200000 долларов США. Наибольшее факторизованное RSA-число имеет длину 768 бит (232 десятичных знака RSA-768) и RSA-2048 может не быть разложено в течение долгих лет, до значительного улучшения вычислительных мощностей и продвижений в факторизации целых чисел.
Успешная факторизация RSA-1024 имеет важное значение для многих пользователей алгоритма RSA аутентификации с открытым ключом, т. к. наиболее часто используемая длина ключа — 1024 бита.
RSA-2048 = 25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357
Вывод
Криптографическая система RSA является безопасной, при правильном подборе секретной информации.
Задачи на будущее.
В настоящее время не существует верной оценки между различными криптосистемами RSA, с точки зрения уровня безопасности [1, с. 178]. Вычисление факторизации чисел RSA-1024, RSA-2048, и других. Планируется изучение диофантовых уравнений, и исследование оценочных алгоритмов в математическом кружке [5, с. 86].
Литература:
- Bakhtiari M. Maarof M. A. — Serious Security Weakness in RSA Cryptosystem // IJCSI International Journal of Computer Science Issues, — 2012 V. 9. Issue 1 No.3. P. 175–178
- Rivest R. L., Shamir A., Adleman L. A method for obtaining digital signatures and public-key cryptosystems // Commun. ACM.-1978.-V. 21, No.2.
- Shor P. Algorithms for Quantum Computation: Discrete Logarithms and Factoring // Foundations of Computer Science, 1994
- Нестеренко Ю. В. Большие вычислительные задачи в теории чисел (Нижний Новгород, 2010) http://www.hpcc.unn.ru/file.php?id=323
- Тагиров К. М. Взаимодействие студентов и школьников в рамках математического кружка при университете // ЛУЧШАЯ СТУДЕНЧЕСКАЯ СТАТЬЯ 2017. — Пенза: Наука и Просвещение, 2017. — С. 84–87.
- Теория чисел: учебник для студ. высш. учеб. заведений / Ю. В. Нестеренко — М.: Издательский центр «Академия», 2008. — 272 с.







