I guess that every one of you once held a piece of paper with entangled passages or walked among the henges trying to find the exit. But perhaps not all of you thought about what mazes can be used for and if it is difficult or not to create an interesting maze.
Mazes are used for many things in our world. Most commonly named usage in, of course, entertainment. But that is not the only use case. Mazes allow children to understand what they see and draw conclusions. Furthermore, mazes teach children to concentrate and develop their patience. In zoology mazes are commonly used in order to understand the way animals think by putting them in a maze with the goal of finding food or another place interesting to them. Knowledge of mazes is also beneficial for cave explorers, as it helps not to get lost.
Not long ago, my brother became interested in completing mazes. He solved all the mazes in his books, and we started printing or drawing him new ones. Over time, it became difficult to find a new maze, so I decided to find a way to generate it myself.
As mazes can be different, the first thing to do was to choose what kind of maze I wanted to generate. I decided to start with a simple rectangular maze m by n squares. Between squares there can be either a wall or a passage. The goal of the maze will be to find the way from the top left square (with coordinates 0, 0) to bottom right square (with coordinates n — 1, m — 1). You can see an example of this type of maze on fig. 1.

Fig. 1
My first goal was to find a way to store the maze. For that, I created a Maze class , which is responsible for storing height ( m ), width ( n ) as well as two lists of wall positions for vertical and horizontal walls.
class Maze:
def __init__(self, width, height):
self.width = width
self.height = height
self.vertical_walls = [[1] * (width + 1) for i in range(height)]
self.horizontal_walls = [[1].copy() * width for i in range(height + 1)]
The next goal was to create a way for me to see the maze, as even if the maze would be created, there is no way to see the result for now. For this, I created several functions that created a window with a picture of the maze, basing it on the data store in class Maze .
def draw(self, m):
self.draw_wall_vertical(m)
self.draw_wall_horizontal(m)
def draw_wall_vertical(self, m):
for i in range(len(m.vertical_walls)):
for j in range(len(m.vertical_walls[i])):
if m.vertical_walls[i][j] == 1:
self.display_walls.create_line(
(j * self.size) + SHIFT,
(i * self.size) + SHIFT,
(j * self.size) + SHIFT,
(i * self.size) + self.size + SHIFT,
fill="black", width=self.size // 5)
def draw_wall_horizontal(self, m):
for i in range(len(m.horizontal_walls)):
for j in range(len(m.horizontal_walls[i])):
if m.horizontal_walls[i][j] == 1:
self.display_walls.create_line(
(j * self.size) + SHIFT,
(i * self.size)+ SHIFT,
(j * self.size) + self.size + SHIFT,
(i * self.size) + SHIFT,
fill="black", width=self.size // 5)
This was enough to get a maze by editing the wall positions manually, but my final goal was to create an autonomous way of generating a maze with minimal user input.
To be able to generate a maze, I decided to start with an algorithm that will generate a simple maze. The way it works can be divided into several steps. Firstly, I create a board for the maze m by n squares. Initially, every pair of adjacent squares has a wall between them and not a single square is considered to be a part of the maze. Then, the square in the top left corner (coordinates 0, 0) was added to the maze, becoming its part and starting point. The next step is to select a random square that is not a part of the maze yet, but is adjacent to it and make it a part of the maze by removing the wall between the maze and this square. This step is repeated in cycle while there are squares that are not a part of the maze. This way, I was able to get a reasonable result. As the maze was “grown” from a starting point, there was a way connecting every two squares, meaning that every square could be considered a start of the goal of the maze. But this type of maze had a lot of branches that ended in a dead end immediately, making them easy to notice. This way, the maze was too easy. You can see examples of the mazes created using this algorithm on fig. 2 and 3.
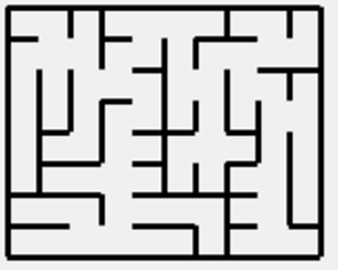
Fig. 2

Fig. 3
In order to make the code work, I created lists is_visited and pool . List is_visited was used to store the coordinates of squares that are already a part of the maze. List pool was used to store all possible pairs of squares, one of which is a part of the maze and the other is not. In the cycle I selected a random element of the list pool and checked if the destination square is not a part of the maze using the list is_visited , which could happen if this square was added to the maze from the other direction. If so, I selected different element of the list pool . When the pair of squares was successfully selected I removed the wall between squares and added the destination square to the maze. This is repeated until the list pool is empty, which will happen when all the squares are a part of the maze.
class Builder():
def __init__(self, width, height):
self.is_visited = [[0] * width for i in range(height)]
self.pool = []
self.width = width
self.height = height
def build(self):
self.maze = Maze(self.width, self.height)
self.visit(0, 0)
while len(self.pool) != 0:
index = random.randint(0, len(self.pool) - 1)
next_visit = self.pool[index]
self.pool[index] = self.pool[-1]
self.pool.pop()
if self.visit(next_visit['target_x'], next_visit['target_y']):
self.remove_wall(next_visit['source_x'], next_visit['source_y'],
next_visit['target_x'], next_visit['target_y'])
return self.maze
def could_visit(self, x, y):
if x < 0 or y < 0 or x >= self.width or y >= self.height:
return False
return True if self.is_visited[y][x] == 0 else False
def visit(self, x, y):
if not self.could_visit(x, y):
return False
self.is_visited[y][x] = 1
if x == self.width - 1 and y == self.height - 1:
return True
self.add_to_queue(x, y, x + 1, y)
self.add_to_queue(x, y, x, y + 1)
self.add_to_queue(x, y, x - 1, y)
self.add_to_queue(x, y, x, y - 1)
return True
def add_to_queue(self, source_x, source_y, target_x, target_y):
if not self.could_visit(target_x, target_y):
return
self.pool.append({
'source_x': source_x,
'source_y': source_y,
'target_x': target_x,
'target_y': target_y,
})
def remove_wall(self, source_x, source_y, target_x, target_y):
if source_x == target_x:
self.maze.horizontal_walls[max(source_y, target_y)][source_x] = 0
else:
self.maze.vertical_walls[source_y][max(source_x, target_x)] = 0
My next goal was to reduce the number of short branches ending in a dead end. For that I modified the previous generation algorithm. Now, I created a straight passage of randomly selected length in a random direction starting from the destination square. The passage continued for a selected number of squares or until it ran into the edge of the board or another part of the maze. Short straight lines can still occur if the length of the line turns out to be equal to 0. This change almost completely removed sort branches. You can see examples of mazes created using this algorithm on fig. 4 and 5.

Fig. 4
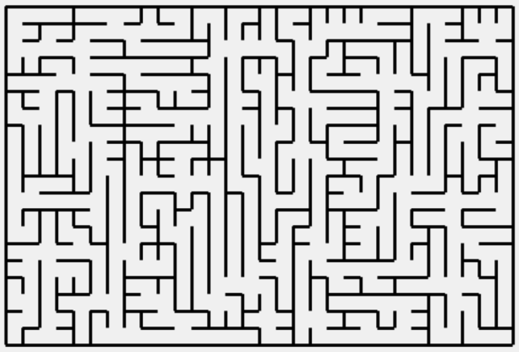
Fig. 5
After this modification, the algorithm was already showing great results, but there still was a problem. As the maze was “grown” from the start, if someone decided to find the way from the end point to the start, they will find that all the branches seem to be merging into one like a tree, which makes it very easy to find the way. Because of that I decided to create a more balanced way of generating the maze, evenly spreading new sections instead of “growing” the maze.
Now, instead of starting from the start, I selected a random point that is not a part of the amaze yet and created two passages of random length — one in random direction and the other in the opposite direction. If the new passage intersected another part of the maze, I connected two parts by removing the wall. The maze generated using this algorithm had almost no short branches and it had a balanced structure, but there were some points that are not connected to the start.
When I create two passages in the opposite directions there is a chance that both of them will intersect the maze. In such cases, if I always connect both sides, the maze will have a large number of cycles and, therefore, ways from start to the goal, making it very easy. But if I always connect only one of the passages, the parts of the maze will not be connected. Because of that, if two intersections occur, I check if there is a connection between two intersected parts. If yes, then I connect only one side. If there is no connection I connect both sides to create connection. You can see examples of mazes created using this algorithm on fig. 6 and 7.
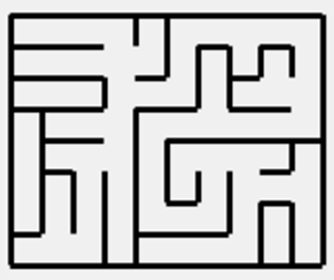
Fig. 6

Fig. 7
The disadvantage of this algorithm is that some parts are isolated from the maze. You can see mazes with such parts are marked in color on fig. 8 and 9. I think that this is not a big issue, as it does not make much difference on the scale it occurs in and can be fixed by removing one wall for each isolated part.
When I was writing the algorithm I needed a way to find out if two parts of the maze are connected or not. For that I created the data structure UnionFind which had two functions.
- Find returns representative of the square. If two squares have the same representative these squares are in the same part of the maze and there is a way connecting them. If the representative is different then there is no way that connects these squares.
- Join joins two different parts of the maze into one. After joining representatives of different squares of joined parts become the same.
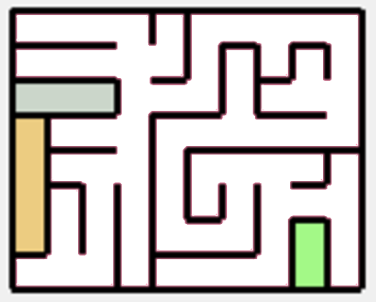
Fig. 8

Fig. 9
When I add a square to the maze, I remove a wall and using Join mark this square as the same part of the maze in the UnionFind data structure. When I am choosing if I should connect a newly generated passage to an intersected part of the maze I use Find to check if this is the same part of the maze or not.
class UnionBuilder():
def __init__(self, width, height):
self.is_visited = [[0] * width for i in range(height)]
self.pool = [[x, y] for x in range(width) for y in range(height)]
self.width = width
self.height = height
self.parent = [[[x, y] for x in range(width)] for y in range(height)]
def root(self, x, y):
if self.parent[y][x] != [x, y]:
self.parent[y][x] = self.root(
self.parent[y][x][0],
self.parent[y][x][1])
return self.parent[y][x]
def build(self):
self.maze = Maze(self.width, self.height)
self.visit(0, 0)
while len(self.pool) != 0:
index = random.randint(0, len(self.pool) - 1)
next_visit = self.pool[index]
self.pool[index] = self.pool[-1]
self.pool.pop()
if not self.visit(next_visit[0], next_visit[1]):
continue
self.add_line(next_visit[0], next_visit[1])
return self.maze
def add_line(self, x, y):
direction = random.randint(0, 3)
direction_coords = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0],
]
dx = direction_coords[direction][0]
dy = direction_coords[direction][1]
self.draw_line(x, y, dx, dy)
self.draw_line(x, y, -dx, -dy)
def draw_line(self, start_x, start_y, dx, dy):
x = start_x
y = start_y
max_size = min(self.width, self.height)
length = max_size // random.randint(2, max_size)
for i in range(length):
x = x + dx
y = y + dy
if x < 0 or y < 0 or x >= self.width or y >= self.height:
break
start_root = self.root(start_x, start_y)
current_root = self.root(x, y)
if start_root != current_root:
self.parent[start_root[1]][start_root[0]] = start_root
self.parent[current_root[1]][current_root[0]] =
start_root
self.remove_wall(x - dx, y - dy, x, y)
if not self.visit(x, y):
break
def could_visit(self, x, y):
if x < 0 or y < 0 or x >= self.width or y >= self.height:
return False
return True if self.is_visited[y][x] == 0 else False
def visit(self, x, y):
if not self.could_visit(x, y):
return False
self.is_visited[y][x] = 1
return True
def remove_wall(self, source_x, source_y, target_x, target_y):
if source_x == target_x:
self.maze.horizontal_walls[max(source_y, target_y)][source_x] = 0
else:
self.maze.vertical_walls[source_y][max(source_x, target_x)] = 0
In order to improve the result, I decided to create a way of rating the maze. I used two criteria: minimal length of the way from the start to the goal and the number of dead ends.
Those criterias that can be calculated automatically allowed me to generate many mazes instead of one and select the best. This not only improved the result but removed mazes with no way from start to the goal as they scored less than those with it. You can compare the result yourself. Mazes on fig. 10 and 11 were generated using the same algorithm, but maze on fig. 10 was the first generated and the maze on fig. 11 was the best out of 100.
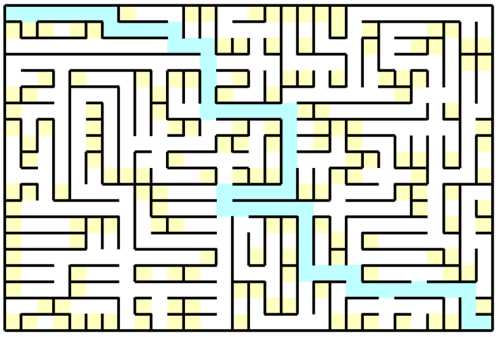
Fig. 10
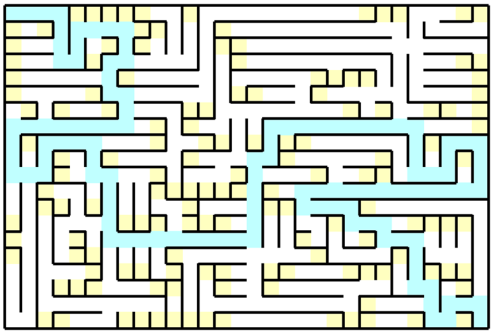
Fig. 11
I want to try improving the way of selecting the best maze out of many. Currently I am comparing entire mazes, but in big mazes some parts are great and others can have some improvements. Maybe, a better idea is to split mazes into parts and compare them independently. Then, a good maze can be assembled out of good parts.
Firstly, I want to try splitting the maze into parts and creating a maze in each of them. Then, I would be able to connect those parts into the whole maze. But I expect a problem here. These parts might be easily distinguishable making the maze easier. This will also limit the variety of mazes that can be generated.
The next idea might be preferable over the previous one. I want to try:
1. Finding the shortest way from start to the goal.
2. Select a random part of this way.
3. Remove it from the maze.
4. Remove all parts that are no longer accessible.
5. Start generating the maze from the current position
6. Compare the previous result to the new one. If the new result is better, use it instead of the previous one.
I expect this to improve the result significantly.
For now, I think that the result is good enough. Even using the initial algorithm, I was able to get a reasonable result, which I was able to improve by expanding the algorithm. Going forward, there are still opportunities to refine approach further, but this version provides a solid foundation for continued development.
References:
- Python's documentation, tutorials, and guides. URL: https://www.python.org/doc/
- Tim Roughgarden, Algorithms Illuminated. Columbia University, New York, 2022.

