Сравнение методов анализа вынужденных электромагнитных колебаний в колебательном контуре. Значение импеданса



В статье автор проводит сравнение двух методов анализа вынужденных электромагнитных колебаний в колебательном контуре и определяет наиболее эффективный из них. Первый метод основан на дедуктивных соображениях и предполагает определение уравнения вынужденных ЭМК. Второй метод зиждется на векторных диаграммах. В процессе будет введен коэффициент «импеданс» или полное электрическое сопротивление.

Ключевые слова: электромагнитные колебания (ЭМК), колебательный контур, векторные диаграммы.

Цель. Выявить наиболее оптимальный способ анализа вынужденных ЭМК.

Задача . В колебательном контуре определить зависимость от времени силы тока и выразить его амплитудное значение двумя методами.

Ниже представлена схема электрической цепи, состоящей из генератора переменного тока (без внутреннего сопротивления), резистора сопротивлением R (оно может включать и сопротивление соединительных проводов), конденсатора емкостью C, катушки индуктивностью L (рис. 1)

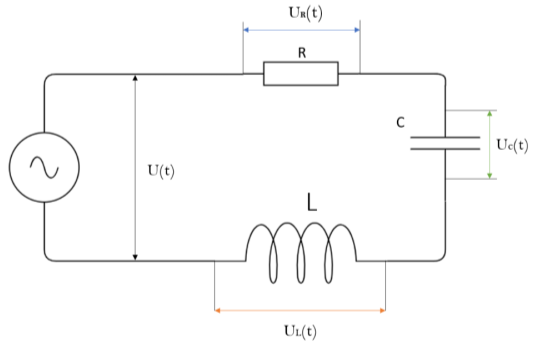
Рис. 1.

Генератор создает ЭДС, пусть на клеммах напряжение U(t), на резисторе UR(t), на конденсаторе UC(t), на катушке ЭДС индукции UL(t).

Записав II правило Кирхгофа, имеем:

UR(t) + UC(t), ( a )

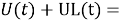
Из следствия закона Фарадея . Помимо этого и , где q — заряд конденсатора, но производной заряда по времени является сила тока, а , значит , .

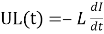
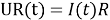
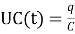
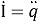
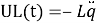
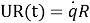
Учитывая , где - амплитудное значение напряжения,

— циклическая частота ЭМК, и подставляя в (a), получаем уравнение вынужденных колебаний: . Если обратиться к механике, то сложно не увидеть сходства в записи уравнения механических колебаний и уравнения вынужденных ЭМК. В связи с этим, минуя трудноописуемые ходы получения результата (так как имеется аналогии с механикой [1, с. 81]) привожу решение уравнения для амплитуды заряда . ; — частота свободных ЭМК и коэффициент . Зная тот факт, что , получаем искомое амплитудное значение силы тока I:

(б). На этом моменте стоит обратить внимание на знаменатель данной дроби, дело в том, что это импеданс — полное электрическое сопротивление, обозначим его буквой . То есть, получено значение коэффициента, который определяет сопротивление системы, а само равенство не что иное, как закон Ома для цепи переменного тока [2,c.25]. К слову, если

, то 0 и если 0. И, что наиболее интересно, при достигается максимальное значение . (см. рис. 2) Действительно, видим, что при достигается максимальное значение. Высота кривых определена сопротивлением R, они становятся ниже при увеличении R.

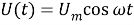
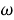
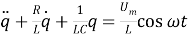
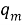
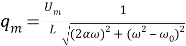
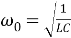
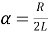
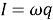
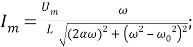
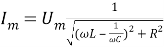
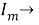
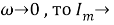
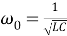
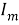
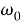
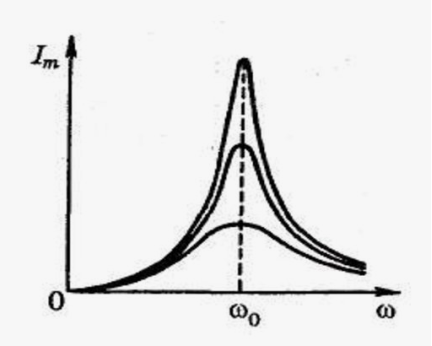
Рис. 2.

Таким образом, мы видим, что использование этого метода хотя и приводит к результату, но требует значительных затрат времени и знания вывода уравнения вынужденных колебаний из механики для проведения аналогий. Поэтому рассмотрим второй, более наглядный метод — метод векторных диаграмм .

Мы знаем, что напряжение в каждом элементе изменяется по гармоническому закону, и эти колебания происходят с одинаковой частотой. Чтобы достичь цели, нам нужно сложить три гармонических колебания одной частоты. Нас интересует зависимость I(t), но так как сила тока одинакова во всех элементах цепи, лучше решить задачу с конца: считать, что ток известен, и найти U(t), складывая колебания с использованием векторных диаграмм. Делаем тоже самое, как и в первом методе, до «(а)»:

(амплитудные значения). Перейдем к действующим значениям, разделив на .В качестве «опоры» используем колебания тока — вектор, описывающий колебания тока в контуре (см. рис. 3).

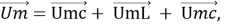
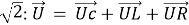
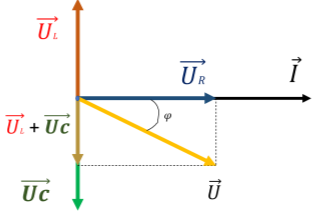
Рис. 3.

Колебания тока через конденсатор опережают колебания напряжения на фазовый угол . Изображаем вектор вниз. Колебания тока через катушку отстают от колебания напряжения на ней ( ). Складываем векторы. Остались несложные действия. По теореме Пифагора:

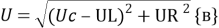
(не имеет значения, как записана разница из-за квадрата). Теперь необходимо вспомнить [2,c.19–22], что , , UR = RI.Подставляем {в} и получаем идентичную (б) формулу.

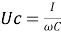
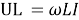
Итак, мы видим, что с помощью минимальных вычислений был получен результат для силы тока в контуре. Метод векторных диаграмм действительно является более быстрым и удобным по сравнению с классическим методом через определения уравнений вынужденных ЭМК.

Таким образом, двумя способами было найдено значение амплитуды силы тока в контуре. Однако стоит учесть, что метод векторных диаграмм является оптимальным, так как он требует меньше времени и не такой общий, как классический метод.

Литература:

1. Вульфсон И. И. Краткий курс теории механических колебаний / И. И. Вульфсон. — Москва: Вестник научно-технического развития, 2017. — 241 c.
2. Физика / А. Т. Глазунов, О. Ф. Кабардин, Н,Малинин и др.; Под ред. А. А. Пинского — 3-е изд. — Москва: Просвещение, 1998. — 432 c.