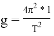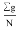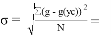Гравитация — одна из самых загадочных и величественных сил природы, которая управляет движением планет, звёзд и галактик. Но как можно измерить гравитацию на Земле, не имея сложных приборов или устройств?
Оказывается, это даже не очень сложно. Для этого достаточно иметь простой маятник, который можно сделать из нитки и груза — именно таким образом великий итальянский учёный Галилео Галилей в XVII веке проводил свои эксперименты, чтобы изучить законы механики и гравитации.
В этом докладе мы пойдём по шагам этого великого учёного и измерим земную гравитацию, тем же способом как сделали это в XVII веке.
Материалы
Для этого эксперимента достаточно иметь под рукой несколько простых вещей, которые мы можем найти в любом доме или школе. Это нитка, грузик, секундомер и немного знаний по физике и математике.
С их помощью мы сможем сделать простой маятник, который будет колебаться под действием силы тяжести. Измеряя время и длину колебаний маятника, мы сможем вычислить гравитацию на Земле с достаточной точностью.
Для этого эксперимента я собрал следующие материалы:
– Нитка известной длины. Я использовал обычную швейную нитку, которую можно купить в любом магазине. Измеряем ее длину с помощью линейки и записываем её в тетрадь.
– Грузик. Я использовал металлический шарик, который можно найти в наборе для игры в настольный бильярд. Измеряем его диаметр с помощью штангенциркуля и также записал его в тетрадь. Радиус шарика нужно прибавить к длине нитки, чтобы получить длину маятника от точки подвеса до центра масс грузика.
– Секундомер. Я использовал свой смартфон, на котором есть функция секундомера.
– Подставка. Подойдёт любая подставка, главное, чтобы она была достаточно высокой и прочной, чтобы выдержать колебания маятника.
Методы
Когда все материалы готовы, мы приступаем к эксперименту. Мы поступали так:
- Привязываем один конец нитки к подставке, а другой конец — к грузику. В итоге мы получили маятник, который можно будет раскачивать в разные стороны.
- Измеряем длину маятника от точки подвеса до центра масс грузика. Для этого мы прибавляем радиус шарика к длине нитки. Записываем в тетрадь.
- Раскачиваем маятник и запускаем секундомер. Считаем, сколько раз маятник проходит через положение равновесия (то есть, когда он вертикален). Когда мы досчитали до 10, останавливаем секундомер. Записываем время, которое показал секундомер, в тетрадь. Это время соответствует 10 колебаниям маятника. Чтобы найти время одного колебания, или период маятника, мы разделяем это время на 10. Записываем период в тетрадь.
- Повторяем предыдущие два шага, удлиняя нить на равномерные промежутки. Измеряем длину маятника и его период для каждого промежутка и записываем их в тетрадь. Мы получаем несколько пар значений: длина маятника и соответствующий период.
- Используем эти значения, чтобы вычислить гравитацию на Земле с помощью аналитического метода
Основа эксперимента
Прежде чем мы начнём, я предлагаю рассмотреть некоторые основные понятия и формулы, которые будут использоваться в расчётах.
Математический маятник — это маленький шарик на невесомой и нерастяжимой нити, размер шарика много меньше, чем длина нити, а масса сосредоточена в центре шарика, то есть шарик принимается как точечная масса.
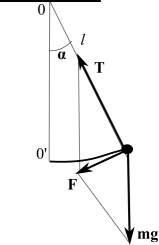
Если сместить шарик из положения равновесия и отпустить его, шарик будет совершать гармонические колебания, проходя по инерции положение равновесия. Колебания будут совершаться по дуге окружности. При этом на маятник действуют следующие силы: сила T — сила натяжения нити, сила mg — сила тяжести и сила F , которая возвращает шарик в положение равновесия. Легко видеть, что
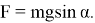
На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную ( F ), меняющую ускорение по величине, и нормальную ( T ), меняющую ускорение по направлению (это центростремительное ускорение, тело движется по дуге). Тангенциальная составляющая ( F ) равна проекции силы тяжести на касательную к траектории. Таким образом при колебании маятника в вертикальной плоскости груз движется ускоренно по дуге под действием равнодействующей силы F , которая меняется при движении, то есть мы наблюдаем ускоренное движение, при котором ускорение меняется с течением времени.
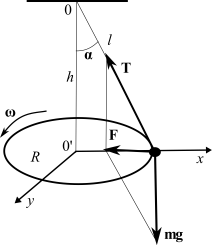
Предположим, что маятник колеблется так, чтобы нить маятника описывала конус и груз двигался по окружности. Это равносильно двум одновременным колебаниям в перпендикулярных направлениях.
Действительно, пусть:
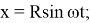
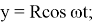
Тогда:
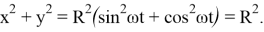
Таким образом сложение двух перпендикулярных колебаний даёт движение по окружности радиуса R . Так как частоты двух колебаний одинаковы, то период обращения по окружности будет равен периоду каждого из обоих колебаний.
Можно назвать это устройство «коническим маятником». Период обращения конического маятника равен отношению длины описываемой грузом окружности к значению его скорости:
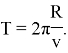
Отклоняющая сила лежит в плоскости вращения, поэтому:
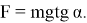
Воспользуемся выражением для малых углов
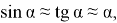
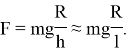
С другой стороны, мы имеем дело с центростремительной силой, поэтому:
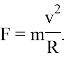
Приравнивая силы, получаем скорость движения по окружности:
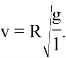
Откуда находим выражения для периода колебаний :
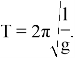
Решаем уравнение относительно g, и вот:
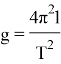
Результаты
Вот полученные данные во время эксперимента, радиус шара = 0.012м, уже добавлен к длине нитки:
|
Длина (м) |
Период (10) (с) |
Период, уср. (10) (c) |
Период (c) |
Период 2 (c) |
|
0.232 |
П1: 9.640 П 2: 9.720 П 3: 9.830 |
9.730 |
0.97 |
0.940 |
|
0.432 |
П 1: 13.050 П 2: 13.280 П 3: 13.230 |
13.180 |
1.320 |
1.740 |
|
0.732 |
П 1: 17.020 П 2: 17.080 П 3: 17.140 |
17.080 |
1.710 |
2.920 |
|
1.032 |
П 1: 20.280 П 2: 20.320 П 3: 20.150 |
20.250 |
2.030 |
4.120 |
|
1.252 |
П 1: 22.070 П 2: 22.440 П 3: 22.530 |
22.350 |
2.240 |
5.010 |
Для большей точности замеряли период по 3 раза.
Расчёты
Используя раннее выведенную формулу —
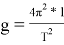
|
Длина (м) |
T 2 (с) |
|
|
0.232 |
0.940 |
9.86 |
|
0.432 |
1.740 |
9.88 |
|
0.732 |
2.920 |
9.89 |
|
1.032 |
4.120 |
9.68 |
|
1.252 |
5.010 |
9.58 |
|
Среднее значение:
|
В следующей таблицы считаем погрешность, используя формулу
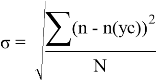
|
Сила Притяжения (м/с 2 ) |
(g-g(ус)) 2 |
|
9.86 |
(9.86–9.78) 2 = 0.0064 |
|
9.88 |
(9.88–9.78) 2 = 0.01 |
|
9.89 |
(9.89–9.78) 2 = 0.0121 |
|
9.68 |
(9.68–9.78) 2 = 0.01 |
|
9.58 |
(9.58–9.78) 2 = 0.04 |
|
|
Из всех выше приведённых расчётов мы получаем что сила притяжения на земле равняется:
9.780 м/с 2 ± 0.183м/с 2
Заключение
В данном реферате мы изучили тему гравитации на Земле и способы её измерения с помощью простого маятника. Используя аналитический метод, мы вывели что гравитация на земле равна 9,780 м/с 2 ± 0.183м/с 2 . Табличное значение гравитации на земле — 9.81 м/с 2 , находится в этом интервале — это значит, что наш эксперимент был успешным и метод достаточно точным, несмотря на его примитивность.