В статье авторы приводят алгоритм шифрования шифром «Double», созданного на основе двух симметричных шифров, и его исследование на криптостойкость.
Ключевые слова: математика, алгоритм, шифр.
Основные симметричные шифры, в которых используются различные математические алгоритмы, рассмотрены в работе [1]. В данной статье представлено описание разработанного авторами нового шифра «Double». Он основан на комбинации шифра «Квадрат Полибия» и шифра Цезаря.
Шифрование шифром «Double» проходит в 3 этапа.
Зашифруем фразу: «АЛЕКСЕЙСОЗДАЛШИФР»
1 этап. Используя принцип шифра «Полибия», представленный в таблице 1, присваиваем каждой букве русского алфавита исходной фразы порядковый номер (представленный в таблице 2).
1-ая цифра — строка, 2-ая цифра — столбец. Т. е. значение каждой буквы имеет 2-е цифры. Например, буква «С» — «28».
Таблица 1
Алфавит для шифра « Double »
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 | |
|
1 |
А |
Б |
В |
Г |
Д |
Е |
Ё |
Ж |
З |
И |
|
2 |
Й |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
|
3 |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ъ |
Ы |
Ь |
|
4 |
Э |
Ю |
Я |
, |
/ |
* |
# |
\ |
+ |
Таблица 2
Таблица преобразования букв в цифры
|
А |
Л |
Е |
К |
С |
Е |
Й |
С |
О |
З |
Д |
А |
Л |
Ш |
И |
Ф |
Р |
|
10 |
22 |
15 |
21 |
28 |
15 |
20 |
28 |
25 |
18 |
14 |
10 |
22 |
35 |
19 |
31 |
27 |
2 этап. Используя принцип шифра «Цезаря», сдвигаем наши «буквы» на 5 знаков. Т. е. присваиваем новые значения номерам букв (смотри таблицу 3).
Таблица 3
Таблица новых значений номеров букв
|
10 |
22 |
15 |
21 |
28 |
15 |
20 |
28 |
25 |
18 |
14 |
10 |
22 |
35 |
19 |
31 |
27 |
|
15 |
27 |
20 |
26 |
33 |
20 |
25 |
33 |
30 |
23 |
19 |
15 |
27 |
40 |
24 |
36 |
32 |
3 этап. Переводим численное значение каждой буквы в соответствующий символ (смотри таблицу 4).
Таблица 4
Таблица зашифрованных букв
|
15 |
27 |
20 |
26 |
33 |
20 |
25 |
33 |
30 |
23 |
19 |
15 |
27 |
40 |
24 |
36 |
32 |
|
Е |
Р |
Й |
П |
Ц |
Й |
О |
Ц |
У |
М |
И |
Е |
Р |
Э |
Н |
Щ |
Х |
Итак, мы зашифровали фразу.
Исходная фраза: «АЛЕКСЕЙСДЕЛАЛПРОЕКТ»
Зашифрованная фраза: «ЕРЙПЦЙОЦУМИЕРЭНЩХ»
Расшифрование проходит в 3 этапа.
Для прочтения зашифрованной фразы абонент должен иметь:
— зашифрованную фразу;
— ключ шифрования (т. е. исходную таблицу алфавита (смотри таблицу 1), а также направление и количество, сдвигов букв).
Расшифруем фразу: «ЕРЙПЦЙОЦУМИЕРЭНЩХ»
1 этап. Находим первую букву из фразы — «Е» (смотри таблицу 1). Фиксируем число, которое соответствует первой букве — «15».
2 этап. «Сдвигаем» букву на 5 знаков влево. Т. е. присваиваем новое значение номеру буквы («15» → «10»).
3 этап. Записываем букву, соответствующей новому значению — «А».
Процесс повторяется до окончания фразы.
Криптостойкость шифра «Double»
Чтобы оценить устойчивость шифра «Double» к расшифрованию, проведен опрос среди учащихся школы.
Условия были одинаковыми для всех учащихся от 6-х до 11-х классов.
В задании было дано зашифрованное слово. На рис. 1 представлена гугл-форма для проверки шифра «DOUBLE» на криптостойкость.
Рис. 1. Форма проверки шифра «DOUBLE» на криптостойкость без подсказки
Без подсказки не было получено ни одного правильного ответа, поэтому на втором этапе проверки на криптостойкость в гугл-форме была дана подсказка в виде алфавита «квадрата Полибия». На рис. 2 представлена гугл-форма для проверки шифра «DOUBLE» на криптостойкость.

Рис. 2. Форма проверки шифра «DOUBLE» на криптостойкость с подсказкой в виде алфавита
На рис. 3 представлена диаграмма ответов учеников 6-х классов. Большинство учащихся не смогли дать правильные ответы, несмотря на подсказку. И только в 8 % случаев ответили правильно.
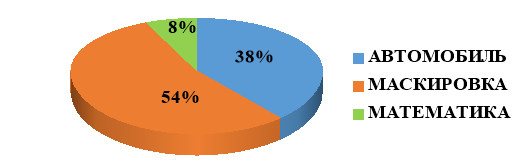
Рис. 3. Диаграмма ответов учеников 6-х классов
На рис. 4 представлена диаграмма ответов учеников 7-х — 11-х классов. Учащиеся, используя подсказку, дали верный ответ в 57 % случаев.
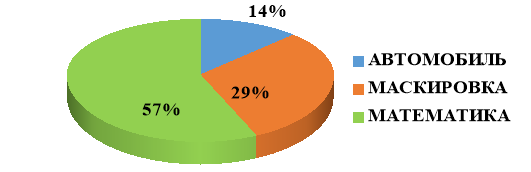
Рис. 4. Диаграмма ответов учеников 7-х — 11-х классов
Благодаря этому исследованию выяснено, что в среде учащихся школы шифр «Double» является криптостойким.
Для использования данного шифра не требуется оборудование. Шифр может быть внедрен в учебный план по курсу «Математика» для учеников 6 класса в рамках изучения курса «Шифры».
Литература:
- Удавцов, А. А. Математические алгоритмы в шифрах / А. А. Удавцов, Ю. В. Азрапкина. — Текст: непосредственный // Юный ученый. — 2023. — № 5 (68). — С. 108–112. — URL: https://moluch.ru/young/archive/68/3716/ (дата обращения: 16.05.2023).

